Números reais

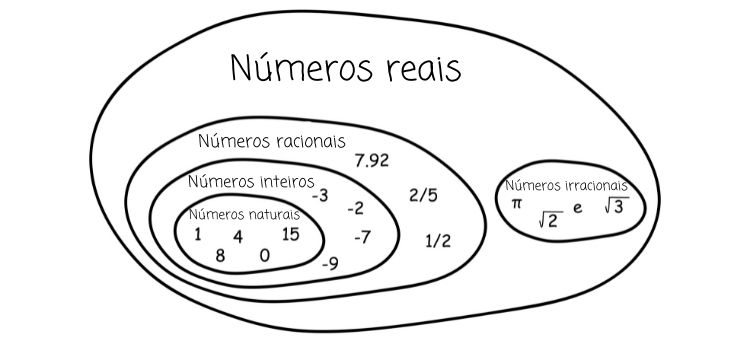
O conjunto dos números reais é a união entre o conjunto dos números racionais e o conjunto dos números irracionais, sendo assim, o número real pode ser um número racional ou um número irracional. Por isso, esse conjunto também contempla o dos números naturais e o dos números inteiros.

O conjunto dos números reais é o mais utilizado no cotidiano, como na realização de medições, no cálculo de funções matemáticas, no estudo de grandezas da física e da química, entre outras situações.

Leia também: Números primos — os números que têm como divisores apenas o número 1 e eles mesmos

Tópicos deste artigo

• 1 - Resumo sobre números reais
• 2 - Quais são os números reais?
  • → Números naturais
  • → Números inteiros
  • → Números racionais
  • → Números irracionais
• 3 - Operações com números reais
• 4 - Propriedades dos números reais
  • → Existência de um elemento neutro na adição e na multiplicação
  • → Propriedade comutativa
  • → Propriedade associativa
  • → Propriedade distributiva
  • → Existência de um inverso na multiplicação
  • → Fechamento para a adição e para a multiplicação
• 5 - Representação dos números reais na reta numérica
• 6 - Exercícios resolvidos sobre números reais

Resumo sobre números reais

• O conjunto dos números reais é a união dos números racionais (que podem ser representados em fração) com os números irracionais (que não podem ser representados em fração).

• Os números racionais são compostos pelos números naturais e números inteiros.

• Podemos calcular as quatro operações com os números reais, e, com base nelas, temos as propriedades específicas dos números reais:

  • existência de um elemento neutro na soma e na multiplicação;

  • propriedade associativa;

  • propriedade comutativa;

  • propriedade distributiva;

  • existência de um elemento inverso na multiplicação;

  • fechamento para a adição e para a multiplicação.  

• Os números reais podem ser representados de forma ordenada na reta real.

Quais são os números reais?

O conjunto dos números reais é a união entre os conjuntos dos números racionais e dos números irracionais (\(\mathbb{R}=\mathbb{Q}\ \bigcup\) \(\mathbb{I}\)), sendo necessário destacar que o conjunto dos números racionais contempla o dos números naturais e o dos números inteiros.

Os números do cotidiano, em sua maioria, são reais, como os que utilizamos para medir peso, altura, temperatura, para fazer contagens, para as nossas relações monetárias, entre outras situações. O conjunto dos números reais não foi o primeiro conjunto numérico a surgir, e, para compreendê-lo, é necessário conhecer os demais conjuntos numéricos.

→ Números naturais

O primeiro conjunto numérico a surgir foi o dos números naturais, que atendeu à necessidade do ser humano de contabilizar e de quantificar objetos. Ele é representado pela letra \(\mathbb{N}\), e os números naturais são:

\(\mathbb{N}={0,\ 1,\ 2,\ 3,\ 4,\ 5...}\ \)

→ Números inteiros

Com o passar do tempo, surgiu a necessidade da representação de números negativos, que não existem nos números naturais, tornando necessária a ampliação do conjunto, dando origem ao conjunto dos números inteiros, composto pelos números naturais e os números opostos a ele. Ele é representado pela letra \(\mathbb{Z}\), e os números inteiros são:

\(\mathbb{Z}={-3,-2,-1,\ 0,\ 1,\ 2,\ 3...}\)

→ Números racionais

O conjunto dos números racionais é formado por todos os números que podem ser escritos na forma de fração. Nele incluímos os números decimais, as dízimas periódicas e os números inteiros.

Diferentemente dos conjuntos supracitados, o conjunto dos racionais não pode ser descrito por uma lista dos termos, pois, entre dois números racionais, sempre existirá outro número racional. Por exemplo, entre 0 e 1, temos 0,5; entre 0 e 0,5, temos o 0,25; entre 0 e 0,25, temos 0,125, e assim sucessivamente. Os números racionais são representados pela letra \(\mathbb{Q}\), são eles:

Essa representação quer dizer que o conjunto dos números racionais (\(\mathbb{Q}\)) é formado pela fração \(\frac{a}{b}\), tal que a pertence ao conjunto dos números inteiros e b pertence ao conjunto dos números inteiros não nulos.

→ Números irracionais

Quando se pensava que o conjunto dos números racionais continha todos os números conhecidos, surge o conjunto dos números irracionais, formado pelos números que não podem ser escritos na forma de fração. Os irracionais são as raízes não exatas e as dízimas não periódicas. Existem números irracionais mais conhecidos, como o número π. Representamos esse conjunto pela letra 𝕀.

Exemplos:

• \(\sqrt3\) (Raíz não exata)

• \(\pi=3,14159\)… (O π é uma dízima não periódica, logo, é um número irracional.)

• 7,12344219023... (Dízima não periódica)

Operações com números reais

As operações com os números reais não possuem nenhuma divergência em relação às operações com os demais conjuntos. Então, com eles, é possível realizar todas as operações, sendo elas: adição, subtração, multiplicação, potenciação e radiciação.

Propriedades dos números reais

Os números reais possuem algumas propriedades importantes. Veja cada uma delas a seguir.

→ Existência de um elemento neutro na adição e na multiplicação

Considere n um número real.

Existe um elemento neutro na soma que é o 0.

n + 0 = n

Existe um elemento neutro da multiplicação entre números reais que é o 1.n · 1 = n

→ Propriedade comutativa

Considere n e m números reais.

Na adição, a ordem das parcelas não altera a soma:

m + n = n + m

Na multiplicação, a ordem dos fatores não altera o produto:m · n = n · m

→ Propriedade associativa

Considere a, m, n números reais.

Na adição de três números, não importa quais números serão somados primeiro.

(a + m) + n = a + (m + n)

Na multiplicação de três números, não importa quais números serão multiplicados primeiro.

(a · m) · n = a · (m · n)

→ Propriedade distributiva

Considere a, m, n números reais.

Na propriedade distributiva, temos que o produto da soma é igual à soma dos produtos.

a (m + n) = am + an

→ Existência de um inverso na multiplicação

Considere n um número real diferente de 0.

Para todo número real n, existe um inverso, \( \frac{1}{n}\), tal que o produto de n pelo seu inverso \(\frac{1}{n}\) é igual ao elemento neutro da multiplicação:

\(n\cdot\frac{1}{n}=1\)

→ Fechamento para a adição e para a multiplicação

O conjunto dos números reais é fechado para a adição e para a multiplicação, isso quer dizer que:

• A soma de dois números reais é um número real.

• A multiplicação entre dois números reais é um número real.

Saiba mais: Adição e subtração de notação científica — como fazer?

Representação dos números reais na reta numérica

Podemos representar os números reais em uma reta, isso possibilita, por exemplo, o desenvolvimento da área da geometria analítica e o estudo de gráficos de funções.

Para essa representação, utilizamos o princípio da boa ordem dos números reais, pois, ao comparar dois números reais distintos, é possível saber qual deles é o maior e então ordená-los. A representação dos números na reta é conhecida como reta numérica ou reta real. O marco zero é conhecido como origem da reta. Para o lado direito, temos os números reais positivos, e, para o lado esquerdo, os números reais negativos.

Exercícios resolvidos sobre números reais

Questão 1

(Vunesp)

Considere a seguinte reta numerada, na qual estão marcados apenas alguns números:

O número representado pela fração -3/2, se fosse colocado nessa reta, ficaria entre:

A) 0 e -1

B) -1 e -2

C) -2 e -3

D) -3 e -4

E) -4 e -5

Resolução:

Alternativa B

Para encontrar a posição da fração, faremos a divisão do numerador pelo denominador para encontrar a forma decimal desse número, então temos que:

-3 : 2 = -1,5

O valor de -1,5 está entre -1 e -2.

Questão 2

O primeiro conjunto a surgir foi o dos números naturais, e, ao longo da história, vários outros foram surgindo para atender à necessidade do ser humano daquela época. Analisando as alternativas a seguir, marque aquela que define corretamente o conjunto dos números reais.

A) É formado pelas frações e as dízimas periódicas.

B) É formado pelos números racionais e os números negativos.

C) É a união do conjunto dos números racionais com o conjunto dos números irracionais.

D) É formado pelos números que não podem ser representados como uma fração.

E) É formado por todos os números positivos, inclusive as raízes não exatas.

Resolução:

Alternativa C

O conjunto dos números reais é a união do conjunto dos números racionais com o conjunto dos números irracionais.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática