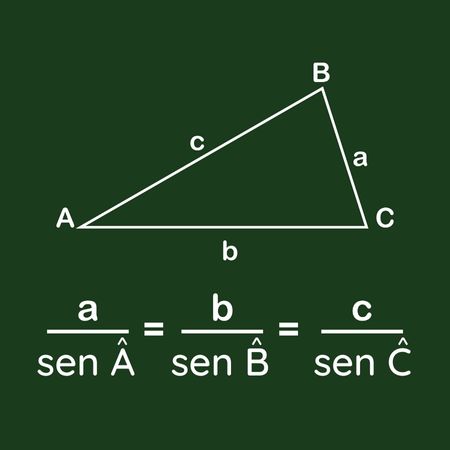
A lei dos senos é uma expressão matemática que relaciona os lados de um triângulo qualquer com seus ângulos. De acordo com esta lei, para um triângulo qualquer, a razão entre cada lado e o seno do ângulo oposto é constante.
Leia também: Secante, cossecante e cotangente — as razões inversas das razões trigonométricas cosseno, seno e tangente
Tópicos deste artigo
- 1 - Resumo sobre lei dos senos
- 2 - Videoaula sobre lei dos senos
- 3 - O que é seno?
- 4 - O que diz a lei dos senos?
- 5 - Qual é a fórmula da lei dos senos?
- 6 - Demonstração e aplicação da lei dos senos
- 7 - Quando se aplica a lei dos senos?
- 8 - Lei dos senos no triângulo retângulo
- 9 - Exercícios resolvidos sobre lei dos senos
Resumo sobre lei dos senos
-
A lei dos senos é uma relação matemática entre os lados e os ângulos de um triângulo qualquer.
-
A fórmula para a lei dos senos é asen \(\frac{a}{sen\hat{A}}=\frac{b}{sen\hat{B}}=\frac{c}{sen\hat{C}}\), em que a, b e c são os lados de um triângulo e \(\hat{A}\), \(\hat{B}\) e \(\hat{C}\) são os ângulos opostos, respectivamente.
-
É interessante aplicar a lei dos senos quando são conhecidos dois ângulos de um triângulo e um dos lados opostos a esses ângulos.
-
Determinar o ângulo de um triângulo por meio da lei dos senos pode ser um processo inconclusivo, pois o seno obtido pode indicar dois ângulos diferentes: um agudo e um obtuso.
Videoaula sobre lei dos senos
O que é seno?
Seno é uma função trigonométrica, e seu valor depende do ângulo considerado. Podemos obter o seno de um ângulo de diferentes maneiras. No caso de um ângulo interior a um triângulo retângulo, o seno é a razão entre o cateto oposto e a hipotenusa.
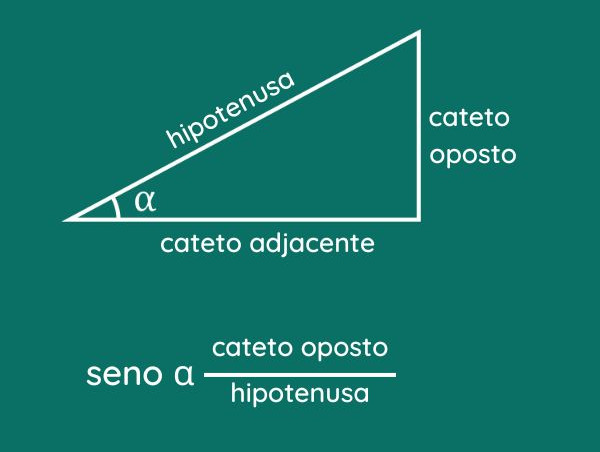
Já para ângulos superiores a 90°, o uso do ciclo trigonométrico é mais indicado. Por exemplo, sabendo que o seno de 30° vale \(\frac{1}2\), concluímos que o seno de 150° também vale \(\frac{1}2\).
O que diz a lei dos senos?
Seja ABC um triângulo qualquer, com lado a oposto ao ângulo \(\hat{A}\), lado b oposto ao ângulo \(\hat{B}\) e lado c oposto ao ângulo \(\hat{C}\).
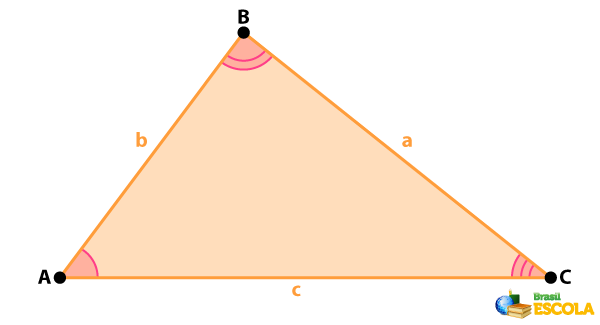
Segundo a lei dos senos, as razões entre cada lado desse triângulo e o seno dos ângulos opostos correspondentes são iguais.
Qual é a fórmula da lei dos senos?
Em notação matemática, para um triângulo ABC com lados opostos medindo a, b e c, respectivamente, a fórmula da lei dos senos é:
\(\frac{a}{sen\hat{A}}=\frac{b}{sen\hat{B}}=\frac{c}{sen\hat{C}}\)
-
Exemplo:
Um triângulo ABC possui ângulos \(\hat{A}=40º\) e \(\hat{B}=20º\). Sabendo que o lado oposto ao vértice A mede 0,5 cm, qual a medida aproximada do lado oposto ao vértice \(\hat{C}\)? Use a aproximação sen 40° = 0,643.
Resolução:
Como a soma dos ângulos de um triângulo é 180°, concluímos que \(\hat{C}=120º\). Seja c o lado oposto ao vértice \(\hat{C}\). Assim, podemos aplicar a lei dos senos relacionando os lados a e c com os senos dos respectivos ângulos opostos:
\(\frac{a}{sen\ \hat{A}}=\frac{c}{sen\ \hat{C}}\)
\(\frac{0,5}{sen\ 40º}=\frac{c}{sen\ 120º}\)
\(0,5⋅\frac{\sqrt3}2=c⋅0,643\)
\(c=0,673\ cm\)
Importante: Note que não foi necessário utilizar as três razões presentes na lei dos senos para resolver o exemplo.
Demonstração e aplicação da lei dos senos
Vejamos de onde vem a lei dos senos e como aplicá-la. Para a demonstração, considere a figura auxiliar abaixo, em que o triângulo ABC é dividido em dois triângulos retângulos com um lado em comum.
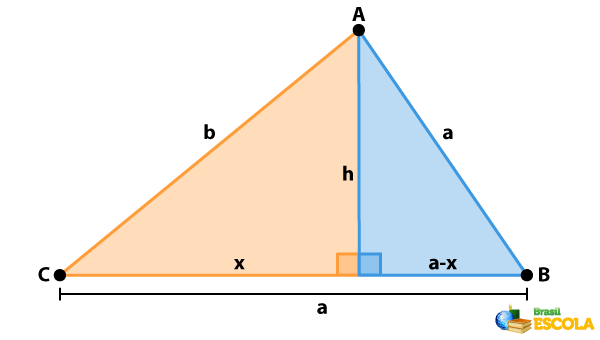
Perceba que sen \(sen\ \hat{C}=\frac{h}B \) e \(sen\ \hat{B}=\frac{h}c\). Ou seja, temos duas expressões para h:
\(h=b⋅sen\ \hat{C}\)
\(h=c⋅sen\ \hat{B}\)
Consequentemente,
\(b⋅sen\ \hat{C}=c⋅sen\ \hat{B}\)
\(\frac{b}{sen\ \hat{B}}=\frac{c}{sen\ \hat{C}}\)
Agora, vamos retornar à figura auxiliar do triângulo ABC e considerar a altura H relativa ao vértice C:
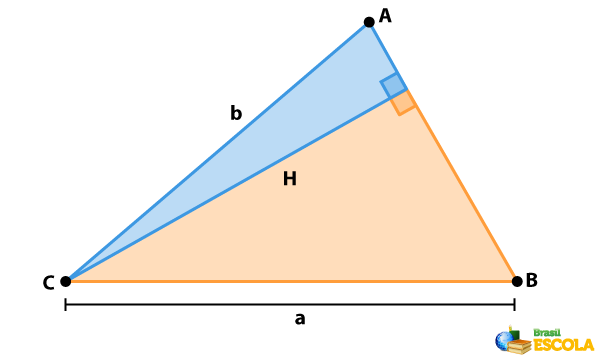
Assim, temos que sen \(sen\ \hat{A}=\frac{H}b\) e \(sen\ \hat{B}=\frac{H}a\). Ou seja:
\(H=b⋅sen\ \hat{A}\)
\(H=a⋅sen\ \hat{B}\)
Consequentemente,
\(b⋅sen\ \hat{A}=a⋅sen\ \hat{B}\)
\(\frac{b}{sen\hat{B}} = \frac{ a}{sen \hat{A}}\)
Combinando esse resultado com a expressão alcançada por meio da primeira figura, obtemos a lei dos senos:
\(\frac{a}{sen\ \hat{A}}=\frac{b}{sen\ \hat{B}}=\frac{c}{sen\ \hat{C}}\)
-
Exemplo:
Anuncie aqui
Se ABC é um triângulo com \(\hat{A}=12°\), \(\hat{C}=150°\) e lado c, oposto a \(\hat{C}\), medindo 5, qual a medida do lado a, oposto a \(\hat{A}\)? Use a aproximação sen 12° = 0,208.
Resolução:Pela lei dos senos:
\(\frac{a}{sen\ \hat{A}}=\frac{c}{sen\ \hat{C}}\)
\(\frac{a}{sen\ 12°}=\frac{5}{sen\ 150°}\)
\(a=2,08\)
Quando se aplica a lei dos senos?
Aplicamos a lei dos senos quando sabemos a medida de dois ângulos e a medida de um dos lados opostos a esses ângulos. Imagine a seguinte situação: dado um triângulo ABC, sabemos a medida de dois lados e de um dos ângulos opostos a um dos lados. Nosso objetivo é determinar a medida do ângulo oposto ao outro lado.
Quando aplicamos a lei dos senos nesse caso, teremos o seno do ângulo procurado. No entanto, esse seno pode corresponder a dois ângulos diferentes. Considere um exemplo em que o resultado obtido foi \(sen\ α=\frac{\sqrt2}2\). Podemos ter \(α=45°\) ou \(α=135°\). Portanto, para a determinação de um ângulo, a lei dos senos não é totalmente eficaz.
Lei dos senos no triângulo retângulo
Considere um triângulo retângulo ABC com catetos medindo a e b e hipotenusa c. Portanto, \(\hat{C}=150°\). Aplicando a lei dos senos e lembrando que sen 90° = 1, concluímos que:
\(\frac{a}{sen\ \hat{A}}=\frac{b}{sen\ \hat{B}}=c\)
Veja também: Os 4 erros mais cometidos na Trigonometria básica
Exercícios resolvidos sobre lei dos senos
Questão 1
(UFPB — adaptado) A prefeitura de certa cidade vai construir, sobre um rio que corta essa cidade, uma ponte que deve ser reta e ligar dois pontos, A e B, localizados nas margens opostas do rio. Para medir a distância entre esses pontos, um topógrafo localizou um terceiro ponto, C, distante 200 m do ponto A e na mesma margem do rio onde se encontra o ponto A. Usando um teodolito (instrumento de precisão para medir ângulos horizontais e ângulos verticais, muito empregado em trabalhos topográficos), o topógrafo observou que os ângulos \(\hat{C}\) e \(\hat{A}\) mediam, respectivamente, 30° e 105°, conforme ilustrado na figura a seguir.
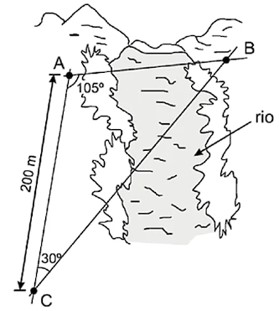
Com base nessas informações, qual a distância, em metros, do ponto A ao ponto B?
Resolução:
Como a soma dos ângulos inteiros de um triângulo é 180°, temos que \(\hat{B}=45º\). Aplicando a lei dos senos:
\(\frac{c}{sen\ \hat{C}}=\frac{b}{sen\ \hat{B}}\)
\(\frac{c}{sen\ 30°}=\frac{200}{sen\ 45°}\)
\(c=100\sqrt2\ m\)
Questão 2:
(Unifor — adaptado) Qual a medida do lado AB do triângulo abaixo?
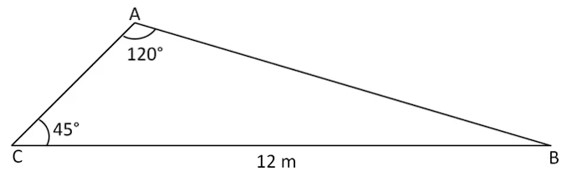
Resolução:
Aplicando a lei dos senos:
\(\frac{c}{sen\ \hat{C}}=\frac{a}{sen\ \hat{A}}\)
\(\frac{c}{sen\ 45°}=\frac{12}{sen\ 120°}\)
\(c=4\sqrt6\ m\)
Por Maria Luiza Alves Rizzo
Professora de Matemática