Aplicações das leis trigonométricas de um triângulo: seno e cosseno

Não há sentido em aprender diversos conceitos matemáticos sem que exista uma compreensão da aplicação destes conceitos, mesmo que em situações hipotéticas. Por hora veremos a aplicação de duas leis trigonométricas que se aplicam em qualquer situação em que se tenha um triângulo, seja ele qual for.

Os conceitos são os das leis do seno e do cosseno, conceitos que trabalham com apenas dois elementos: ângulo e medida do lado.

Veremos uma mesma situação, onde um construtor de pontes deseja calcular o tamanho da ponte que será construída, entretanto, em cada uma das situações as informações serão diferentes. Com isso veremos os casos nos quais é possível a aplicação da Lei do Seno e da Lei do Cosseno.

Situação 1) O construtor deseja calcular a distância do ponto A ao ponto C, pontos onde a ponte será construída, entretanto ele não possui nenhuma ferramenta que meça essa distância, mas ele conhece de matemática e teve a seguinte ideia. “Como eu possuo uma ferramenta que calcula ângulos, conseguirei determinar o comprimento desta ponte”. Com isso ele marcou um ponto B, calculou o ângulo BÂC que foi igual a 85°, caminhou até o ponto B, uma distância de 2km, e calculou o ângulo ABC obtendo um ângulo de 65°. O construtor acredita que com essas informações será possível calcular o comprimento da ponte.

Veja como será realizado esse cálculo:

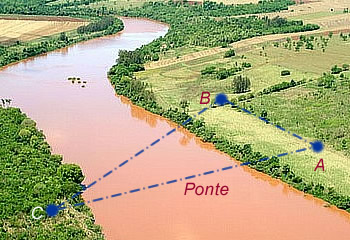
Note que as únicas informações dadas foram:

Vejamos as expressões das Leis trigonométricas que podem ser aplicadas.

Lei do seno:

Lei do cosseno:

Veja que com os dados que temos não é possível aplicar a lei do cosseno, pois precisamos das medidas de dois lados e temos apenas a medida de um lado e de dois ângulos, portanto, aplicaremos a lei dos senos.

O objetivo é determinar o valor do segmento AC, sendo assim utilizaremos as duas últimas proporções.

Situação 2) O construtor deseja calcular a distância do ponto A ao ponto C, pontos onde a ponte será construída, entretanto, com a ferramenta que ele possui só foi possível calcular as medidas dos segmentos AB e BC, no qual o segmento AB é igual a 2km e o segmento BC 3,99km. Utilizou novamente a ferramenta de medir ângulos e obteve que o ângulo do vértice B é igual a 65°. Com isso, o construtor conseguiu determinar o comprimento da ponte. Faça você também esses cálculos.

Vejamos as informações que temos:

Temos a medida de dois lados e apenas um ângulo. Um fato importante que nos permite aplicar a lei dos cossenos é o ângulo informado ser determinado pelos dois lados que são conhecidos.

Assim, devemos nos atentar às informações que a situação nos passa, para que saibamos qual relação devemos utilizar. Esse é o ponto crucial para diferenciar essas duas leis quanto à sua aplicação.

Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola