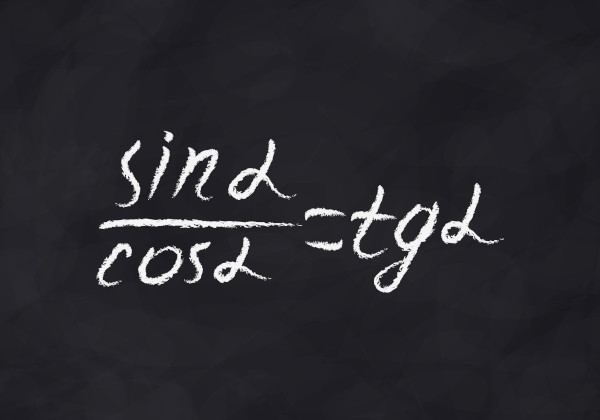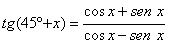Conhecemos como transformações trigonométricas as fórmulas que facilitam o cálculo do valor de seno, cosseno e tangente para a soma e a diferença entre arcos, a resolução de problemas envolvendo arco duplo, e a reescrita de uma adição de razões trigonométricas como um produto.
Com as transformações trigonométricas, é possível aumentar o número de valores conhecidos para as razões trigonométricas, pois, com base nos dois arcos conhecidos, é possível encontrar o valor do seno, cosseno e tangente da soma ou da diferença entre os ângulos conhecidos por meio das transformações trigonométricas. As principais transformações trigonométricas são a soma e a diferença entre arcos, as fórmulas para arco duplo, e as transformações em produtos.
Leia também: Quais são os 4 erros mais cometidos na trigonometria básica?
Tópicos deste artigo
- 1 - Resumo sobre as transformações trigonométricas
- 2 - O que são as transformações trigonométricas?
- 3 - Fórmulas das transformações trigonométricas
- 4 - Transformação em produto
- 5 - Exercícios resolvidos sobre transformações trigonométricas
Resumo sobre as transformações trigonométricas
-
As transformações trigonométricas são fórmulas que facilitam nos cálculos de razões trigonométricas para alguns arcos.
-
Utilizamos as transformações trigonométricas para calcular o seno, o cosseno e a tangente da soma e da diferença de dois arcos.
O que são as transformações trigonométricas?
Conhecemos como transformações trigonométricas as fórmulas utilizadas para encontrar o valor das razões trigonométricas de seno, cosseno e tangente, em alguns casos particulares, para a soma ou diferença entre dois arcos, em um arco duplo, e também para a transformação da adição ou da diferença entre arcos em um produto entre arcos.
Fórmulas das transformações trigonométricas
Vejamos, a seguir, as fórmulas das transformações trigonométricas.
-
Soma e diferença de dois arcos
Para calcular a soma ou a diferença entre dois arcos trigonométricos, utilizamos as fórmulas:
1) seno da soma:
sen(a + b) = sen(a) · cos (b) + sen (b) · cos (a)
2) seno da diferença:
sen(a – b) = sen(a) · cos (b) – sen (b) · cos (a)
3) cosseno da soma:
cos(a + b) = cos(a) · cos (b) – sen (a) · sen (b)
4) cosseno da diferença:
cos(a – b) = cos(a) · cos (b) + sen (a) · sen (b)
5) tangente da soma:
![]()
6) tangente da diferença:
![]()
Exemplo:
Durante a medição de determinados ângulos, encontrou-se as medidas de 50º e 30º, e, calculado o valor do seno e do cosseno desses ângulos, temos:
sen 30º = 0,50
cos 30º = 0,87
sen 50º = 0,77
cos 50º = 0,64
Com base nesses dados, calcule:
a) sen 80º
Sabemos que 80º = 30 + 50º, então, temos que:
sen(80º) = sen(30º + 50º)
Utilizando a fórmula do seno da soma, temos que:
sen(a + b) = sen(a) · cos(b) + sen(b) · cos(a)
sen(30° + 50°) = sen(30°) · cos(50º) + sen(50°) · cos(30°)
sen(80º) = 0,50 · 0,64 + 0,77 · 0,87
sen(80°) = 0,32 + 0,6699
sen(80º) = 0,9899
b) cos (20º)
Sabemos que 20º = 50º – 30º, então, temos que:
cos 20º = cos (50º – 30º)
Utilizando a fórmula para o cosseno da diferença, temos que:
cos(a – b) = cos(a) · cos (b) + sen (a) · sen (b)
cos(50° – 30°) = cos(50°) · cos (30°) + sen (50°) · sen (30°)
cos(20°) = 0,64 · 0,87 + 0,77 · 0,50
cos(20°) = 0,64 · 0,87 + 0,77 · 0,50
cos(20º) = 0,5568 + 0,385
cos(20º) = 0,9418
Veja também: Seno e cosseno de ângulos suplementares
-
Arco duplo
Encontramos as fórmulas para o arco duplo quando vamos realizar a soma de dois arcos iguais:
1) seno do arco duplo:
sen(2a) = 2sen(a) · cos(a)
2) cosseno do arco duplo:
cos(2a) = cos(a)² – sen(a)²
3) tangente do arco duplo:
![]()
Exemplo:
Sabendo que tg 20º = 0,47, então, calcule o valor da tg 40º.
Sabemos que 40° = 2 · 20°, então, utilizando a fórmula da tangente do arco duplo, temos que:
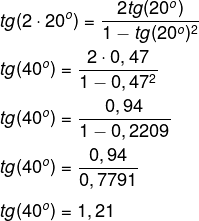
Transformação em produto
Com as fórmulas a seguir, é possível transformar a soma ou a diferença entre as razões trigonométricas como um produto.
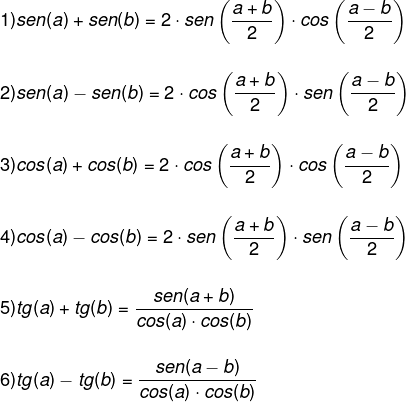
Exercícios resolvidos sobre transformações trigonométricas
Questão 1 - Utilizando os ângulos notáveis, o valor cos 15º é:
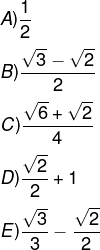
Resolução
Alternativa C
Sabemos que 15º = 45º – 30º.
Então, temos que:
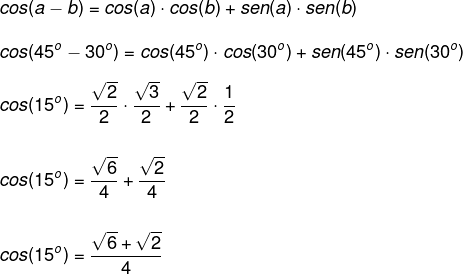
Questão 2 - (Unifenas) Sendo dados sen(x) = 0,8 e cos(x) = 0,6, qual é o valor do sen(2x)?
A) 0,96
B) 0,90
C) 0,80
D) 0,70
E) 0,60
Resolução
Alternativa A
Utilizando a fórmula do arco duplo:
sen(2x) = 2sen(x) · cos(x)
Substituindo os valores conhecidos:
sen(2x) = 2 · 0,8 · 0,6
sen(2x) = 0,96
Por Raul Rodrigues de Oliveira
Professor de Matemática