Identidades trigonométricas

As identidades trigonométricas são relações entre funções trigonométricas. A tangente e a identidade fundamental são os principais exemplos dessas relações, existindo, ainda, as funções secante, cossecante e cotangente.

Leia também: Transformações trigonométricas — as fórmulas que facilitam o cálculo de algumas razões trigonométricas

Tópicos deste artigo

• 1 - Resumo sobre identidades trigonométricas
• 2 - Quais são as identidades trigonométricas?
• 3 - Demonstrações das identidades trigonométricas
  • → Demonstração da tangente
  • → Demonstração da identidade fundamental da trigonometria
• 4 - Outras identidades trigonométricas
• 5 - Exercícios resolvidos sobre identidades trigonométricas

Resumo sobre identidades trigonométricas

• As identidades trigonométricas são igualdades que relacionam funções trigonométricas.
• Os principais exemplos de identidades trigonométricas são a tangente e a identidade fundamental.
• A tangente de um ângulo  é igual à razão entre o seno de  e o cosseno de Â, desde que cos não seja nulo.
• A identidade fundamental da trigonometria determina que a soma entre o quadrado do seno de um ângulo  e o quadrado do cosseno de  é 1.
• Outros exemplos de identidades trigonométricas são as funções secante, cossecante e cotangente.

Quais são as identidades trigonométricas?

As identidades trigonométricas são igualdades que associam funções trigonométricas. As principais são a tangente (tan) e a identidade fundamental da trigonometria:

• Tangente: a tangente de um ângulo θ é igual à razão entre o seno de θ e o cosseno de θ, em que cos θ≠0:

\(tan\ \theta=\frac{sen\ \theta}{cos\ \theta}\)

• Identidade fundamental da trigonometria: também conhecida como identidade de Pitágoras, estabelece uma relação entre o seno e o cosseno de um ângulo θ. De acordo com essa identidade, a soma entre \(\left(sen\ \theta\right)^2 e \left(cos\ \theta\right)^2\) é igual a 1. Escrevendo \(\left(sen\ \theta\right)^2=sen^2\ \theta\) e \(\left(cos\ \theta\right)^2=cos^2\ \theta\), temos que:

\(sen^2\ \theta\ +\ cos^2\ \theta\ =1\)

Como aplicar as identidades trigonométricas?

Podemos aplicar as identidades trigonométricas quando, para certo ângulo θ, desconhecemos o valor de uma das funções.

• Exemplo 1

Utilizando as aproximações sen 40°≈0,643 e cos 40°≈0,766, determine o valor de tan 40° com três casas decimais.

Resolução:

Utilizando a identidade trigonométrica da tangente:

\(tan\ 40°=\frac{sen 40°}{cos 40°}\)

\(tan\ 40°=\frac{0,643}{0,766}\)

\(tan\ 40°=0,839\)

• Exemplo 2

Se θ é um ângulo do segundo quadrante e sen θ≈0,956, encontre o valor de cos θ com três casas decimais.

Resolução:

Utilizando a identidade fundamental da trigonometria:

\(sen^2\ \theta+cos^2\ \theta=1\)

\(\left(0,956\right)^2+cos^2\theta=1\)

\(0,913936+cos^2\theta=1\)

\(cos^2\theta=0,086064\)

\(cos\ \theta=\pm\sqrt{0,086064}\)

Como θ é um ângulo do segundo quadrante, então o valor do cos θ é negativo, portanto:

\(cos\ \theta=-\ \sqrt{0,086064}\)

\(cos\ \theta=-0,293\)

Demonstrações das identidades trigonométricas

→ Demonstração da tangente

A demonstração da identidade trigonométrica \(tan\ \theta=\frac{sen\ \theta}{cos\ \theta}\) segue da definição de tangente na circunferência trigonométrica de raio 1.

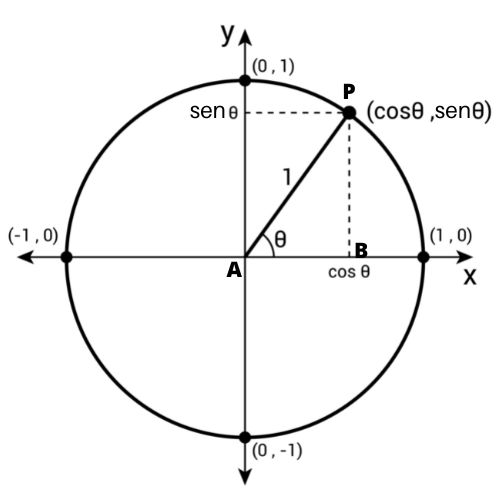
Observe que as coordenadas de P são x=cos θ e y=sen θ. Por definição, \(tan\ \theta=\frac{y}{x}\), assim:

\(tan\ \theta=\frac{sen\ \theta}{cos\ \theta}\)

→ Demonstração da identidade fundamental da trigonometria

A demonstração da identidade trigonométrica sen² θ + cos² θ = 1 também se baseia na circunferência trigonométrica. Na imagem anterior, observe que o triângulo ABP é retângulo em B e que AB=cos θ, BP=sen θ e AP=1. Aplicando o teorema de Pitágoras nesse triângulo, concluímos que:

\(sen^2\ \theta+cos^2\ \theta=1\)

Outras identidades trigonométricas

As funções secante (sec), cossecante (cossec ) e cotangente (cotan) também são exemplos de identidades trigonométricas:

\(sec\ \theta=\frac{1}{cos\ \theta}\)

\(cossec\ \theta=\frac{1}{sen\ \theta}\)

\(cotan\ \theta=\frac{1}{tan\ \theta}=\frac{cos\ \theta}{sen\ \theta}\)

Associando essas funções com a identidade de Pitágoras, podemos construir outras identidades trigonométricas:

\(sec^2\theta=1+tan^2\ \theta\)

\(cossec^2\theta=1+cotan^2\ \theta\)

Saiba mais: Aplicações trigonométricas na Física

Exercícios resolvidos sobre identidades trigonométricas

Questão 1

Considere que cos θ≠1. Assim, a expressão \(\frac{sen^2\ \theta}{1-cos\ \theta}\) é igual a qual alternativa?

A) cos θ

B) 1 + cos θ

C) sen θ

D) 1 + sen θ

E) tan θ

Resolução

Alternativa B

Reescrevendo a identidade trigonométrica fundamental, temos que \(sen^2\theta=1-cos^2\theta\). Assim:

\(\frac{sen^2\theta}{1-cos\ \theta}=\frac{1-cos^2\theta}{1-cos\ \theta}\)

Como \(1=1^2\), podemos reescrever o numerador:

\(1-cos^2\theta=1^2-cos^2\theta=\left(1-cos\ \theta\right).\left(1+cos\ \theta\right)\)

Portanto:

\(\frac{1-cos^2\ \theta}{1-cos\ \theta}=\frac{\left(1-cos\ \theta\right).\left(1+cos\ \theta\right)}{\left(1-cos\ \theta\right)}\ =\ 1\ +\ cos\ \theta\)

Questão 2

Se sen θ≠0 e cos θ≠0, determine o valor de a=sec θ ∙ cos θ + cossec θ ∙ sen θ.

Resolução

Substituindo sec \(\theta=\frac{1}{cos\ \theta} \) e cossec \(\theta=\frac{1}{sen\ \theta}\) na expressão de a, temos que:

\(a=\ \frac{1}{cos\ \theta}\cdot cos\ \theta+\ \frac{1}{sen\ \theta}\cdot seno\ \theta=1+1=2\)

Logo, a=2

Por Maria Luiza Alves Rizzo
Professora de Matemática