Função

Estabelecemos uma função quando relacionamos uma ou mais grandezas. Parte dos fenômenos naturais pode ser estudada graças ao desenvolvimento nessa área da matemática. O estudo das funções é dividido em duas partes, temos a parte geral, em que estudamos os conceitos gerais, e a parte específica, em que estudamos os casos particulares, como as funções polinomiais e as funções exponenciais.

Veja também: Como construir o gráfico de uma função?

Tópicos deste artigo

• 1 - O que é função?
• 2 - Domínio, contradomínio e imagem de uma função
• 3 - Função sobrejetiva
• 4 - Função injetiva
• 5 - Função bijetora
• 6 - Função composta
• 7 - Função par
• 8 - Função ímpar
• 9 - Função crescente
• 10 - Função decrescente
• 11 - Função constante
• 12 - Função afim
• 13 - Função quadrática
• 14 - Função modular
• 15 - Função exponencial
• 16 - Função logarítmica
• 17 - Funções trigonométricas
• 18 - Função raiz

O que é função?

Uma função é uma aplicação que relaciona os elementos de dois conjuntos não vazios. Considere dois conjuntos não vazios A e B, em que uma função f relaciona cada elemento de A a um único elemento de B.

Para entender melhor essa definição, imagine uma corrida de táxi. Para cada viagem, ou seja, para cada distância percorrida, existe um preço diferente e único, isto é, não tem sentido uma viagem ter dois preços diferentes.

Podemos representar essa função que leva elementos do conjunto A para o conjunto B das seguintes maneiras.

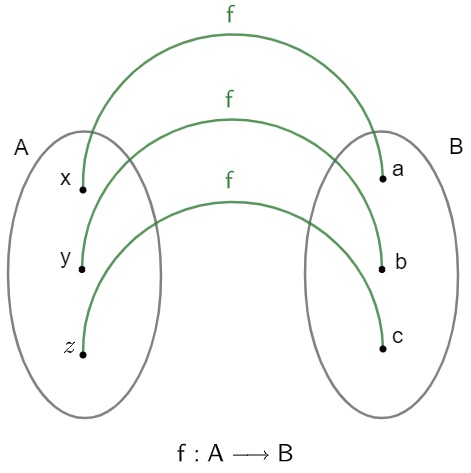
Observe que, para cada elemento do conjunto A, existe um único elemento relacionado com ele no conjunto B. Agora podemos pensar, afinal, quando uma relação entre dois conjuntos não será uma função? Bom, quando um elemento do conjunto A relacionar-se com dois elementos distintos de B, ou quando sobrar elementos do conjunto A sem se relacionarem com elementos de B. Veja:

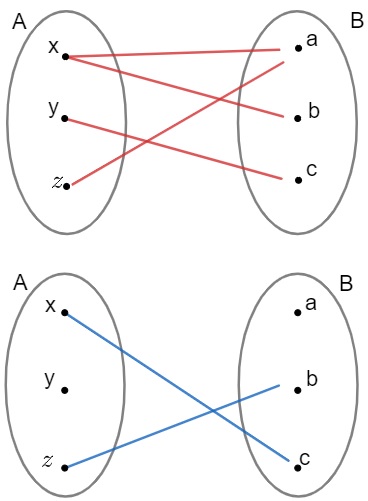
De modo geral, podemos escrever uma função de maneira algébrica assim:

f: A → B

x → y

Note que a função pega elementos do conjunto A (representados por x) e leva-os aos elementos de B (representados por y). Podemos também dizer que os elementos do conjunto B são dados em função dos elementos do conjunto A, logo, podemos representar y por:

y = f(x)

Lê-se: (y igual f de x)

Domínio, contradomínio e imagem de uma função

Quando temos uma função f, os conjuntos que estão sendo relacionados recebem nomes especias. Assim, considere uma função f que leva elementos do conjunto A para os elementos do conjunto B:

f: A → B

O conjunto A, do que partem as relações, é denominado domínio da função, e o conjunto que recebe as “flechas” dessa relação é chamado de contradomínio. Denotamos esses conjuntos da seguinte maneira:

D_f = A → Domínio de f
CD_f = B → Contradomínio de f

O subconjunto do contradomínio de uma função formado por elementos que se relacionam com elementos do conjunto é denominado imagem da função e é denotado por:

Im_f → Imagem de f

• Exemplo

Considere a função f: A → B representada no diagrama a seguir e determine o domínio, o contradomínio e a imagem.

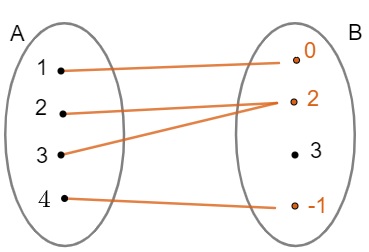
Como foi dito, o conjunto A = {1, 2, 3, 4} é o domínio da função f, enquanto o conjunto B = {0, 2, 3, –1} é o contradomínio da mesma função. Agora, observe que o conjunto formado por elementos que recebem a flecha (em laranja) formado pelos elementos {0, 2, –1} é subconjunto do contradomínio B, esse conjunto é a imagem da função f, assim:

D_f = A = {1, 2, 3, 4}

CD_f = B = {0, 2, 3, –1}

Im_f = {0, 2, –1}

Dizemos que o 0 é imagem do elemento 1 do domínio, assim como o 2 é imagem dos elementos 2 e 3 do domínio, e –1 é imagem do elemento 4 do domínio. Para saber mais detalhes sobre esses três conceitos, leia: Domínio, contradomínio e imagem.

Função sobrejetiva

Uma função f: A → B será sobrejetiva ou sobrejetora se, e somente se, o conjunto imagem coincidir com o contradomínio, ou seja, se todos elementos do contradomínio são imagens.

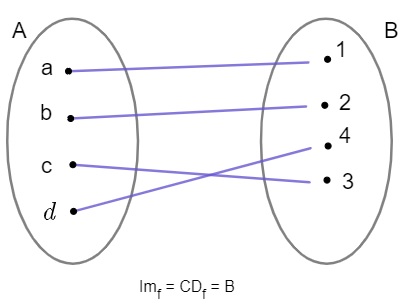
Dizemos então que uma função é sobrejetora quando todos elementos do contradomínio recebem flechas. Se quiser aprofundar-se mais nesse tipo de função, acesse o nosso texto: Função sobrejetora.

Função injetiva

Uma função f: A → B será injetiva ou injetora se, e somente se, elementos distintos do domínio possuírem imagens distintas no contradomínio, isto é, imagens iguais são geradas por elementos iguais do domínio.

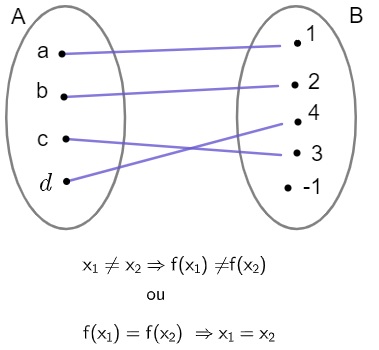
Veja que a condição é que elementos distintos do domínio relacionem-se com elementos distintos do contradomínio, não havendo problema em sobrar elementos no contradomínio. Para compreender melhor esse conceito, você pode ler o texto: Função injetora.

Função bijetora

Uma função f: A → B será bijetora se, e somente se, ela for injetora e sobrejetora simultaneamente, ou seja, elementos distintos do domínio possuem imagens distintas, e a imagem coincide com o contradomínio.

• Exemplo

Em cada um dos casos, justifique se a função f(x) = x² é injetora, sobrejetora ou bijetora.

a) f: ℝ₊ → ℝ

Observe que o domínio da função são todos os reais positivos e que o contradomínio são todos os números reais. Sabemos que a função f é dada por f(x) = x², agora imagine todos os números reais positivos sendo elevados ao quadrado, todas as imagens serão também positivas. Assim podemos concluir que a função é injetora e não sobrejetora, pois os números reais negativos não vão receber flechas.

Ela é injetora, pois cada elemento do domínio (ℝ₊) relaciona-se apenas com um elemento do contradomínio (ℝ).

b) f: ℝ → ℝ₊

A função, nesse caso, possui o domínio como sendo todos os reais e o contradomínio como sendo os reais positivos. Sabemos que qualquer número real elevado ao quadrado é positivo, logo, todos os elementos do contradomínio receberam flechas e, assim, a função é sobrejetora. Ela não será injetora pelo fato de elementos do domínio relacionarem-se com dois elementos do contradomínio, por exemplo:

f(–2) = (–2)² = 4

f(2) = (2)² = 4

c) f:ℝ₊ → ℝ₊

Nesse exemplo a função possui domínio e contradomínio como sendo os números reais positivos, logo, a função é bijetora, pois cada número real positivo relaciona-se com um único número real positivo do contradomínio, nesse caso o quadrado do número. Além disso, todos os números do contradomínio receberam flechas.

Função composta

A função composta está associada com a ideia de atalho. Considere três conjuntos não vazios A, B e C. Considere também duas funções f e g, em que a função f leva elementos x do conjunto A para elementos y = f(x) do conjunto B, e a função g leva os elementos y = f(x) para elementos z do conjunto C.

A função composta recebe esse nome por ser uma aplicação que leva elementos do conjunto A direto para elementos do conjunto C, sem passar pelo conjunto B, por meio da composição das funções f e g. Veja:

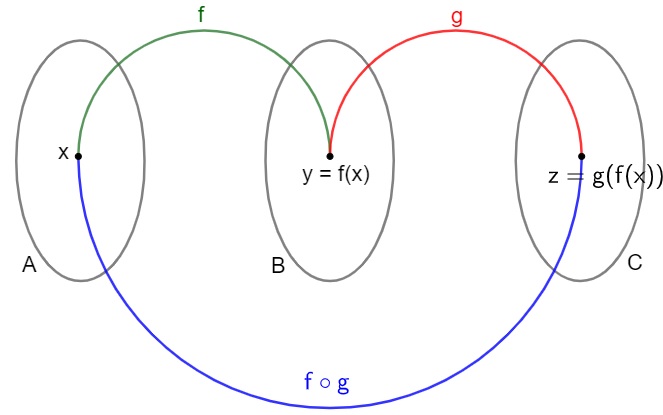
A função denotada por (f o g) leva os elementos do conjunto A diretamente para o conjunto C. Ela é chamada de função composta.

• Exemplo

Considere a função f (x) = x² e a função g(x) = x + 1. Determine as funções compostas (f o g)(x) e (g o f)(x).

A função f o g é dada pela função g aplicada na f, ou seja:

(f o g)(x) = f(g(x))

Para determinar essa função composta, devemos considerar a função f, e, no lugar da variável x, devemos escrever a função g. Veja:

x²

(x+1)²

(f o g)(x) = f(g(x)) = x² + 2x + 1

De maneira análoga, para determinar a função composta (g o f)(x), devemos aplicar a função f na função g, ou seja, considerar a função g e escrever a função f no lugar da variável. Veja:

(x + 1)

x² + 1

Portanto, a função composta (g o f)(x) = g (f(x)) = x² + 1.

Função par

Considere uma função f: A → ℝ, em que A é um subconjunto dos reais não vazio. Uma função f será par somente para todo x real.

• Exemplo

Considere a função f: ℝ → ℝ, dada por f(x) = x².

Veja que para qualquer valor de x real, se elevado ao quadrado, o resultado é sempre positivo, ou seja:

f(x) = x²

e

f(–x) = (–x)² = x²
 

Portanto, f(x) = f(–x) para qualquer valor de x real, assim, a função f é par.

Leia também: Propriedades das potências – quais são e como as utilizar?

Função ímpar

Considere uma função f: A → ℝ, em que A é um subconjunto dos reais não vazio. Uma função f será ímpar somente para todo x real.

• Exemplo

Considere a função f: ℝ → ℝ, dada por f(x) = x³.

Veja que para qualquer valor de x podemos escrever que (–x)³ = –x³. Confira alguns exemplos:

(–2)³ = –2³ = –8

(–3)³ = –3³ = –27

Assim podemos afirmar que:

f(–x) = (–x)³ = –x³

f(–x) = (–x)³ = –f(x)

Portanto, para qualquer x real f(–x) = –f(x), e assim a função f(x) = x³ é ímpar.

Função crescente

Uma função f é crescente em um intervalo se, e somente se, à medida que os elementos do domínio crescem, suas imagens também crescem. Veja:

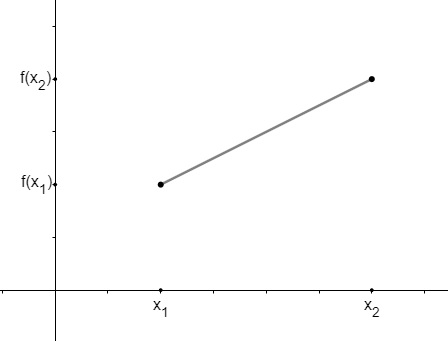
Observe que x₁ > x₂ e o mesmo ocorre com a imagem, assim, podemos estabelecer uma condição algébrica para que a função f seja crescente.

Função decrescente

Uma função f é decrescente em um intervalo se, e somente se, à medida que os elementos do domínio crescem, suas imagens decrescem. Veja:

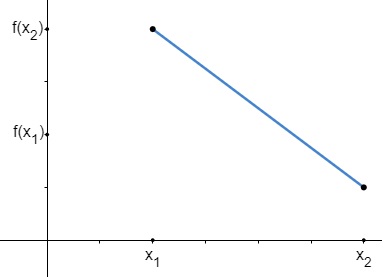
Veja que, no domínio da função, temos que x₁ > x₂, entretanto isso não ocorre na imagem da função, em que f(x₁) < f(x₂). Assim podemos estabelecer uma condição algébrica para funções decrescentes. Veja:

Função constante

Como o próprio nome diz, uma função é constante quando, para qualquer valor do domínio, o valor da imagem é sempre o mesmo.

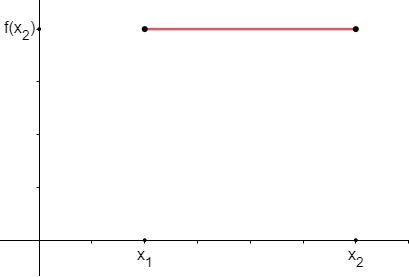
Função afim

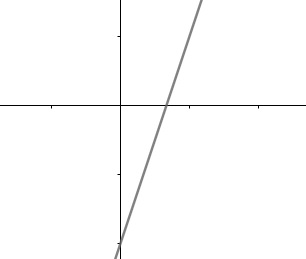
A função afim ou polinomial do primeiro grau é escrita na forma:

f(x) = ax + b

Em que a e b são números reais, a é diferente de zero, e o seu gráfico é uma reta. A função possui domínio real e contradomínio também real.

Função quadrática

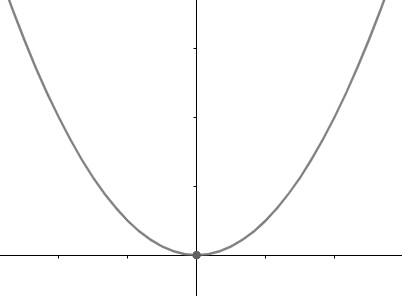
A função quadrática ou função polinomial do segundo grau é dada por um polinômio de grau dois, assim:

f(x) = ax² + bx + c

Em que a, b e c são números reais com a diferente de zero, e seu gráfico é uma parábola. A função também possui domínio e contradomínio reais.

Função modular

A função modular com variável x encontra-se dentro do módulo e algebricamente é expressa por:

f(x) = |x|

A função também possui domínio e contradomínio reais, ou seja, podemos calcular o valor absoluto de qualquer número real.

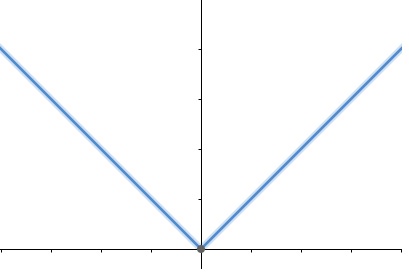
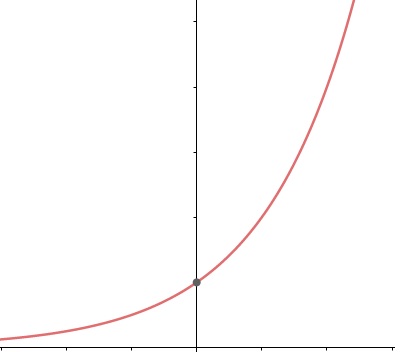
Função exponencial

A função exponencial apresenta a variável x no expoente. Ela também possui domínio real e contradomínio real e é descrita algebricamente por:

f(x) = a^x

Em que a é um número real maior que zero.

Função logarítmica

A função logarítmica possui a variável no logaritmando e o domínio formado por números reais maiores que zero.

Funções trigonométricas

As funções trigonométricas possuem a variável x envolvendo as razões trigonométricas, as principais são:

f(x) = sen(x)

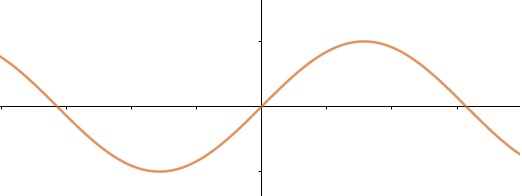
f(x) = cos(x)

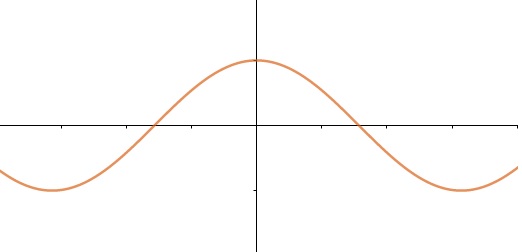
f(x) = tg(x)

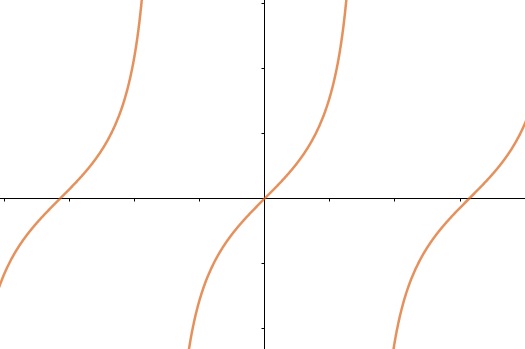
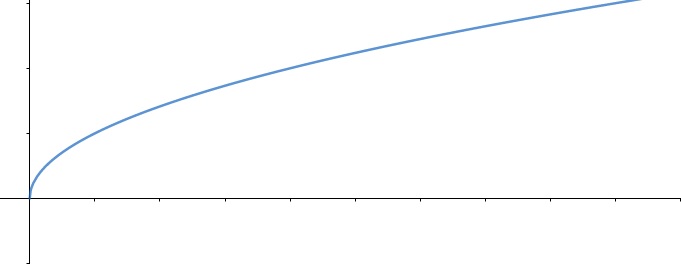
Função raiz

A função raiz é caracterizada por ter a variável no interior da raiz, com isso, se o índice da raiz for par, o domínio da função passa a ser somente os números reais positivos.

 

Por Robson Luiz
Professor de Matemática