Parábola

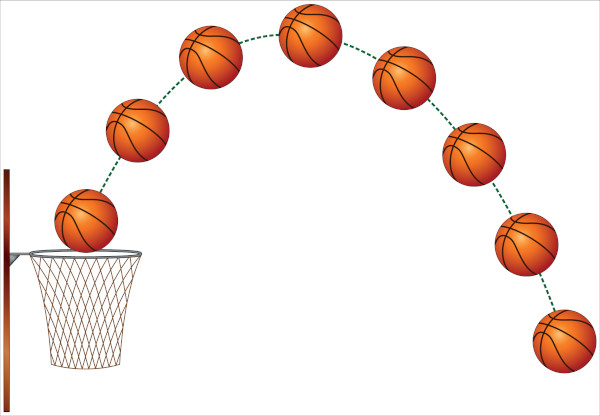
Parábola é o gráfico de uma função do segundo grau (também chamada de função quadrática). Seu formato é curvo, semelhante à letra U, podendo ser mais “aberta” ou “fechada” dependendo dos coeficientes da função do segundo grau que a definem. A parábola pode assumir posições diferentes, também de acordo com a função do segundo grau correspondente.

Os principais elementos da parábola são o foco, a reta diretriz, o eixo e o vértice, comumente representados no plano cartesiano.

Leia também: Afinal, o que é uma função do segundo grau?

Tópicos deste artigo

• 1 - Resumo sobre a parábola
• 2 - O que é parábola?
• 3 - Exemplos de parábola
• 4 - Elementos de uma parábola
• 5 - Propriedade refletora da parábola
• 6 - Equações reduzidas da parábola
• 7 - Aplicações da parábola
• 8 - Exercícios resolvidos sobre parábola

Resumo sobre a parábola

• A parábola é o gráfico de uma função quadrática. Seus pontos estão à mesma distância de um ponto chamado de foco e de uma reta chamada de reta diretriz. O ponto médio entre o foco e a reta diretriz é chamado de vértice da parábola.
• A concavidade e a posição de uma parábola estão diretamente relacionadas com os coeficientes da função do segundo grau que a definem.
• Exemplos de aplicação da parábola são as antenas parabólicas, os faróis dos automóveis e a descrição do movimento uniformemente variado.

O que é parábola?

Parábola é gráfico de uma função do segundo grau (ou função quadrática). Ao contrário da reta, que é o gráfico de uma função do primeiro grau, não é possível desenhar com exatidão uma parábola conhecendo-se alguns de seus pontos. No entanto, para o estudo da parábola, é suficiente construir um esboço com base na função quadrática que a determina.

Mas antes de relacionar diretamente uma parábola com sua função, vejamos a definição matemática dessa curva. Formalmente, uma parábola é o conjunto dos pontos equidistantes a uma reta d  (chamada de reta diretriz) e um ponto fixo F  (chamado de foco) que não esteja na reta. Atenção: a distância de um ponto a uma reta é o segmento perpendicular a ela passando pelo ponto. Na imagem a seguir, PQ é distância do ponto P (um ponto sobre a parábola) até a reta diretriz d . Consequentemente, pela definição da parábola, PQ = PF.

Todos os pontos P sobre a parábola estão à mesma distância de d e F.

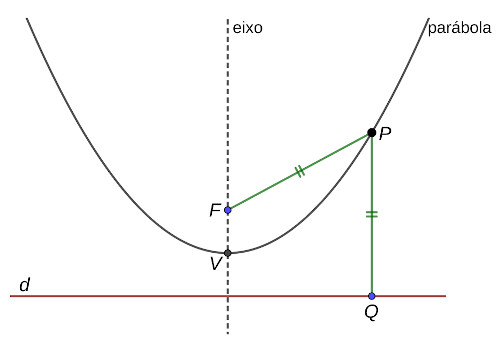
Chamamos de eixo da parábola a reta perpendicular à reta diretriz passando pelo foco. Ainda, o ponto da parábola mais próximo da reta diretriz é chamado de vértice da parábola. Uma característica importante do vértice é que ele é o ponto médio entre o foco e o ponto de interseção do eixo com a reta diretriz.

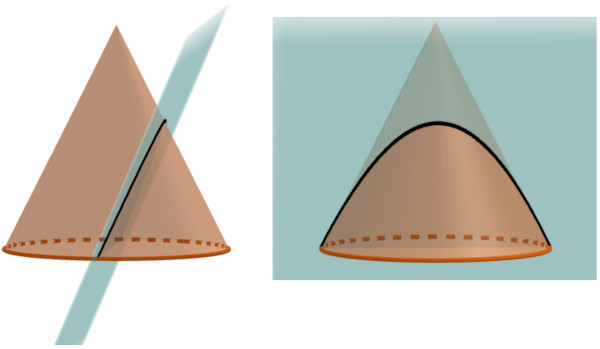
Curiosidade: A parábola também pode ser definida como a curva resultante da interseção de um cone com um plano paralelo a uma de suas geratrizes.

Exemplos de parábola

Na maioria dos casos, estudamos parábolas com eixo vertical. Consequentemente, essas parábolas podem ter concavidade para cima ou concavidade para baixo. Observe os exemplos de parábolas a seguir, cujos eixos coincidem com o eixo das ordenadas (eixo y) do plano cartesiano.

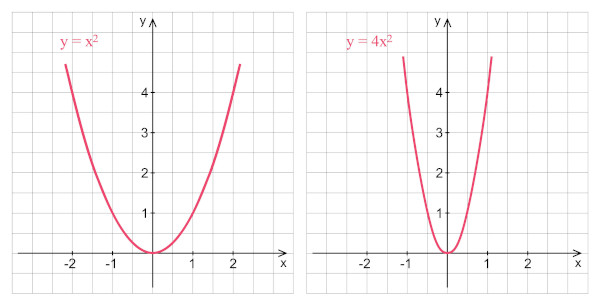
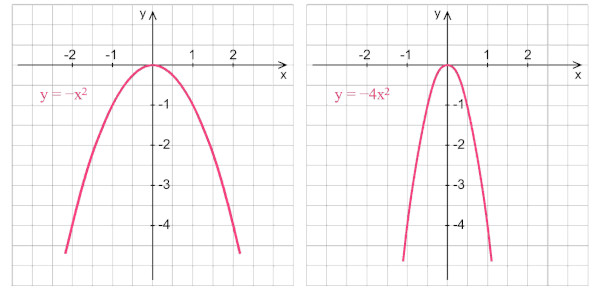
Dada a função que caracteriza uma parábola, é possível determinar seu formato e algumas características. Para isso, devemos analisar os coeficientes da função. Considere uma função do segundo grau f(x) = ax² + bx + c  com determinante Δ = b² -4ac .

 Assim, podemos concluir que:

• Se a > 0, a concavidade da parábola é para cima.
• Se a < 0, a concavidade da parábola é para baixo.
• O coeficiente c  determina onde a parábola cruza o eixo das ordenadas.
• Se Δ > 0, a parábola cruza o eixo das abscissas em dois pontos.
• Se Δ = 0, a parábola cruza o eixo das abscissas em um ponto.
• Se Δ < 0, a parábola não cruza o eixo das abscissas.

Saiba mais: Relação entre parábola e coeficientes de uma função do segundo grau

Elementos de uma parábola

Os principais elementos de uma parábola são:

• Reta diretriz: a reta que compõe a definição.
• Foco: ponto fora da reta diretriz que compõe a definição.
• Eixo: reta perpendicular à reta diretriz. Esse elemento também é conhecido como eixo de simetria, pois divide a parábola em duas partes iguais.
• Vértice: ponto médio entre a reta diretriz e o foco.
• Parâmetro: distância entre o foco e a reta diretriz.

Propriedade refletora da parábola

A propriedade mais famosa da parábola está relacionada ao foco. Essa propriedade estabelece que raios incidentes paralelos ao eixo são refletidos para o foco.

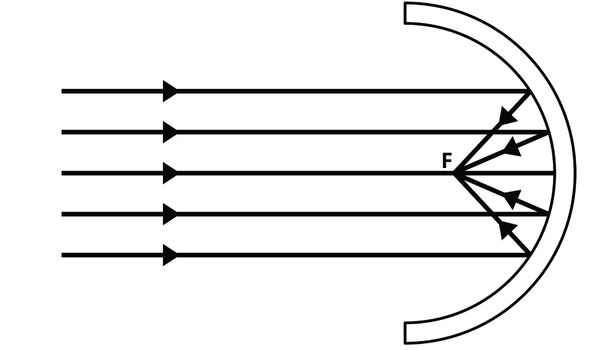
Algo semelhante ocorre com as ondas sonoras. Consequente, essa propriedade é muito utilizada pelas antenas parabólicas, que possuem o formato de um paraboloide de revolução (ou superfície parabólica). Tal formato é obtido por meio da rotação de uma parábola.

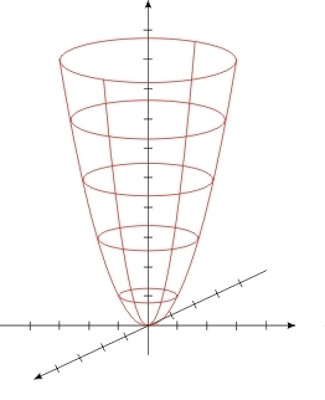
Assim, a antena parabólica amplifica os sinais fracos recebidos por satélite ao convergi-los para o foco.

Além disso, a propriedade “contrária” também é válida: raios emitidos pelo foco são espalhados em direções paralelas ao eixo. Alguns instrumentos são construídos para funcionar com base nessa ideia, como lanternas de mão, holofotes e faróis de automóveis.

Equações reduzidas da parábola

As equações reduzidas da parábola são obtidas pela definição dessa figura. Se P = (x, y) é um ponto da parábola, então a distância de P até a reta diretriz d é igual à distância de P até o foco F. Assim, basta utilizar as expressões de distância entre dois pontos e distância entre ponto e reta.

Vejamos as duas principais equações reduzidas da parábola, que consideram a reta diretriz paralela ao eixo x, o vértice V na origem e p como metade do parâmetro (portanto, p é a distância do vértice ao foco ou, de maneira equivalente, do vértice à reta diretriz).

• Se a parábola possui concavidade voltada para cima, eixo vertical sobre o eixo das abscissas, vértice V = (0, 0) e reta diretriz r = -p  , então sua equação reduzida é x² = 4py .
• Se a parábola possui concavidade voltada para baixo, eixo vertical sobre o eixo das abscissas, vértice V = (0, 0) e reta diretriz r = p  , então sua equação reduzida é x² = -4py .

Exemplo: Qual a equação reduzida de uma parábola com vértice (0, 0) em que o foco está no semieixo positivo das ordenadas e possui parâmetro 4?

Observe que, nessas condições, a parábola possui eixo vertical sobre o eixo das abscissas e reta diretriz no semieixo negativo das ordenadas, além de concavidade voltada para cima. Como o parâmetro é 4, p = 2 . Portanto, sua equação reduzida é x² = 8y , em que P= (x,  y)  são pontos da parábola.

Cuidado: Alguns autores utilizam a letra p para indicar todo o parâmetro (e não metade, como fizemos aqui). Consequentemente, as equações reduzidas da parábola ficam um pouco diferentes, ainda que a teoria de construção seja exatamente a mesma. Para compreender melhor esse assunto, confira o texto: Cônicas.

Aplicações da parábola

Além dos usos associados à propriedade refletora, a parábola possui outra aplicação superimportante: descrever a posição de objetos em relação ao tempo no movimento uniformemente variado (MUV).

Nesse tipo de movimento, um corpo altera sua velocidade segundo uma aceleração constante. Assim, a expressão que descreve sua posição (normalmente representada por S) em relação ao tempo (normalmente representado por t) forma uma parábola.

Saiba mais: Estudo dos gráficos do movimento uniformemente variado

Exercícios resolvidos sobre parábola

Questão 1

(PUC RS 2017) O morro onde estão situadas as emissoras de TV em Porto Alegre pode ser representado graficamente, com algum prejuízo, em um sistema cartesiano, através de uma função polinomial de grau 2 da forma y = ax² + bx + c , com a base da montanha no eixo das abscissas.

Para que fique mais adequado essa representação, devemos ter:

a) a > 0 e b² – 4ac > 0

b) a > 0 e b² – 4ac < 0

c) a < 0 e b² – 4ac < 0

d) a < 0 e b² – 4ac > 0

e) a < 0 e b² – 4ac = 0

Solução: Alternativa D

Como a concavidade é virada para baixo, o coeficiente a deve ser menor do que zero. Ainda, como a parábola corta o eixo das abscissas na base da montanha em dois pontos, o determinante deve ser maior do que zero.

Questão 2

(Enem) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.

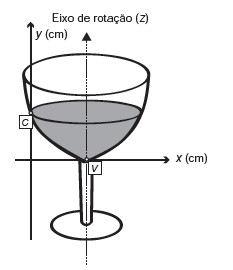
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei \(f\left(x\right)=\frac{3}{2}x^2-6x+C\) em que C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.

Nessas condições, a altura do líquido contido na taça, em centímetros, é

a) 1

b) 2

c) 4

d) 5

e) 6

Solução: Alternativa E

Como a parábola toca o eixo das abscissas em um ponto, o determinante deve ser igual a zero. Portanto, \(b^2-4ac=0\), ou seja, \({(-6)}^2-4\frac{3}{2}C=0\), logo, C = 6.

Por Maria Luiza Alves Rizzo
Professora de Matemática