Relação da parábola com o delta da função do segundo grau

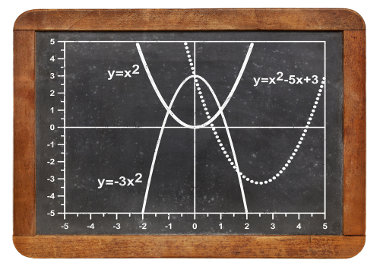
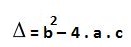A parábola é o gráfico da função do segundo grau (f(x) = ax² + bx + c), também chamada de função quadrática. Ela é traçada no plano cartesiano, que possui como coordenadas x (abscissas = eixo x) e y (ordenadas = eixo y).

Para traçarmos o gráfico de uma função quadrática, é preciso descobrir quantas raízes ou zeros reais a função possui em relação ao eixo x. Entenda raízes como a solução da equação do segundo grau que pertence ao conjunto dos números reais. Para sabermos a quantidade de raízes, é preciso calcular o discriminante, que é chamado de delta e é dado pela seguinte fórmula:

A fórmula do discriminante/delta é feita em relação aos coeficientes da função do segundo grau. Sendo assim, a, b e c são os coeficientes da função f(x) = ax² + bx + c .

Existem três relações da parábola com o delta da função do segundo grau. Essas relações estabelecem as seguintes condições:

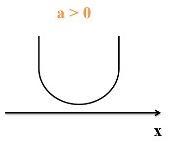
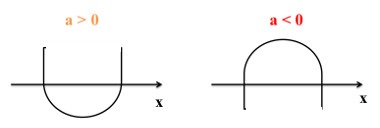
• Primeira condição: Quando Δ > 0, a função possui duas raízes reais diferentes. A parábola interceptará o eixo x em dois pontos distintos.

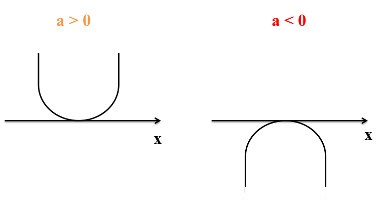
• Segunda condição: Quando Δ = 0, a função possui uma única raiz real. A parábola tem somente um ponto em comum, que tangencia o eixo x.

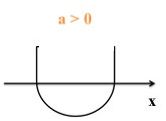
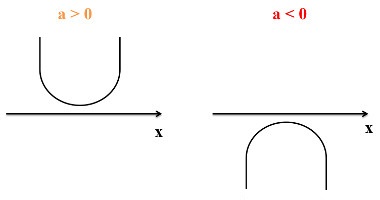
• Terceira condição: Quando Δ < 0, a função não possui raiz real; logo, a parábola não intercepta o eixo x.

Concavidade da Parábola

O que determina a concavidade da parábola é o coeficiente a da função de segundo grau – f(x) = ax² + bx + c. A parábola tem a concavidade voltada para cima quando o coeficiente é positivo, ou seja, a > 0. Caso seja negativo (a < 0), a concavidade fica voltada para baixo. Para compreender melhor as condições estabelecidas anteriormente, observe os esboços das parábolas a seguir:

• Para Δ > 0:

• Para Δ = 0:

• Para Δ < 0.

Vamos praticar os conceitos aprendidos, observe os exemplos abaixo:

Exemplo: Encontre o discriminante de cada função do segundo grau e determine a quantidade de raízes, a concavidade da parábola e esboce o gráfico da função em relação ao eixo x.

a) f(x) = 2x² – 18
b) f(x) = x² – 4x + 10
c) f(x) = - 2x² + 20x – 50

Resolução

a) f(x) = x² – 16

Inicialmente, devemos verificar os coeficientes da função do segundo grau:

a = 2, b = 0, c = - 18

Substitua os valores dos coeficientes na fórmula do discriminante/delta:

Como o delta é igual a 144, ele é maior que zero. Sendo assim, aplica-se a primeira condição, isto é, a parábola interceptará o eixo x em dois pontos distintos, ou seja, a função possui duas raízes reais diferentes. Como o coeficiente é maior do que zero, a concavidade fica para cima. O esboço do gráfico está logo abaixo:

b) f(x) = x² – 4x + 10

Inicialmente, devemos verificar os coeficientes da função do segundo grau:

a = 1, b = - 4, c = 10

Substitua os valores dos coeficientes na fórmula do discriminante/delta:

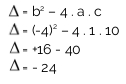
O valor do discriminante é - 24 (menor que zero). Com isso, aplicamos a terceira condição, isto é, a parábola não intercepta o eixo x, logo, a função não possui nenhuma raiz real. Como a > 0, a concavidade da parábola fica para cima. Observe o esboço do gráfico:

c) f(x) = - 2x² + 20x – 50

Inicialmente, devemos verificar os coeficientes da função do segundo grau.

a = - 2, b = 20, c = - 50

Substitua os valores dos coeficientes na fórmula do discriminante/delta:

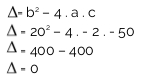
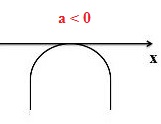
O valor de delta é 0, logo, aplica-se a segunda condição, isto é, a função possui uma única raiz real, e a parábola tangencia o eixo x. Como a < 0, a concavidade da parábola fica para baixo. Veja o esboço do gráfico:

Por Naysa Oliveira
Graduada em Matemática