As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação.
Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características em uma função é preciso que tenhamos o conhecimento da definição de função, do que é um domínio, imagem e contradomínio.
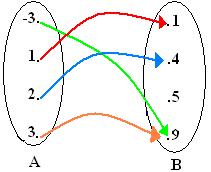
Observe o diagrama abaixo que representa uma função f: A→B e veja quem é o domínio, a imagem e o contradomínio dela.
Domínio serão todos os elementos do conjunto A: D(f) = {-3,1,2,3} a imagem será os elementos do conjunto B que receberem a seta: Im(f) = {1,4,9} e o contradomínio será todos os elementos do conjunto B: CD(f) = {1,4,5,9}.
Agora, veja como identificar essas características da função:
Função sobrejetora
Uma função será sobrejetora se o conjunto imagem for igual ao conjunto do contradomínio, ou seja, o conjunto imagem será todos os elementos do conjunto de chegada. Matematicamente, podemos dizer que: f: A →B definida por uma fórmula qualquer será sobrejetora se Im(f) = B.
Função injetora
Uma função será injetora se os elementos do conjunto do domínio estiverem ligados a imagens distintas. Matematicamente podemos dizer que: f: A → B definida por uma fórmula qualquer será injetora se todos os elementos de A forem distintos (diferentes) e as imagens desses elementos forem distintas também.
Função bijerora
Para que uma função assuma a característica de uma função bijetora ela tem que ser ao mesmo tempo sobrejetora e injetora. O conjunto imagem deverá ser igual ao conjunto do contradomínio e todos os elementos do domínio deverão estar ligados a imagens distintas.
Por Danielle de Miranda
Graduada em Matemática