Função constante

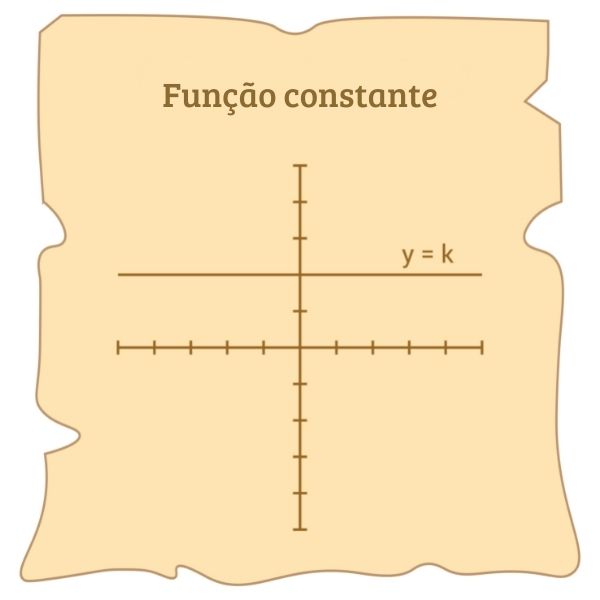
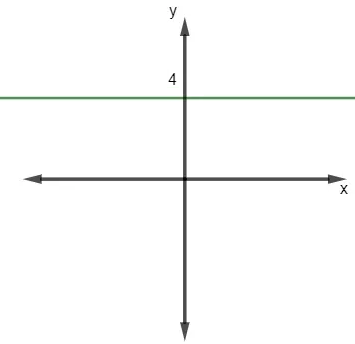
A função constante é um caso particular de função. Dados o domínio e o contradomínio no conjunto dos números reais, a função constante é a função que possui lei de formação igual a f(x) = k, em que k é um número real. Essa lei de formação nos mostra que independentemente do valor da variável x, a imagem da função será igual a k. Assim, ao realizar a representação gráfica da função constante, encontraremos uma reta paralela ao eixo horizontal.

Leia também: Domínio, contradomínio e imagem de uma função

Tópicos deste artigo

• 1 - Resumo sobre função constante
• 2 - O que é uma função constante?
• 3 - Gráfico da função constante
• 4 - Exercícios resolvidos sobre função constante

Resumo sobre função constante

• A função constante é um caso particular de função.

• A lei de formação da função constante é f(x) = k, em que k é um número real.

• A imagem de todos os valores do domínio de uma função constante é sempre igual à constante k.

• O gráfico da função constante é uma reta paralela ao eixo x.

O que é uma função constante?

No estudo das funções, existe um caso particular de função conhecido como função constante. Dada uma função com domínio no conjunto dos números reais e contradomínio no conjunto dos números reais, a função constante é a função que possui lei de formação f(x) = k, em que k é um número real.

Ela recebe o nome de constante porque independentemente do valor de x, f(x) será sempre igual a k, ou seja, para todo valor de x, a imagem será k.

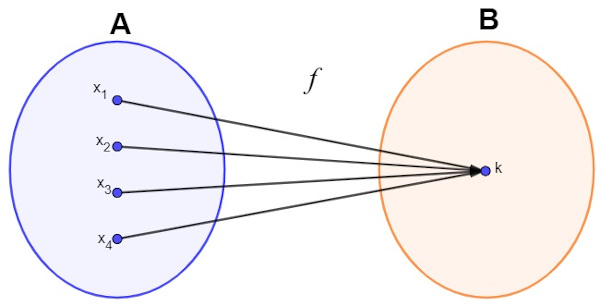
No diagrama, podemos perceber que para diferentes valores de x, a imagem é sempre a mesma, ou seja, f(x) = k.

Considerando as funções com domínio e contradomínio no conjunto dos números reais, em uma função constante o valor de k pode ser qualquer número real, como nos exemplos de lei de formação de funções constantes a seguir:

• f(x) = 2

• f(x) = π

• f(x) =  \( -\ \sqrt2\)

• f(x) = -  0,3

• f(x) = \(\frac{1}{5}\)

Gráfico da função constante

De modo geral, o gráfico de uma função constante será sempre uma reta. Supondo que a constante é um número real diferente de zero e que essa reta é sempre paralela ao eixo horizontal do plano cartesiano, ou seja, do eixo x, caso a constante k seja igual a zero, o gráfico será uma reta em cima do eixo x. Veja a representação gráfica de algumas funções constantes a seguir.

Dada a função constante com lei de formação f(x) = 5, há a seguinte representação gráfica:

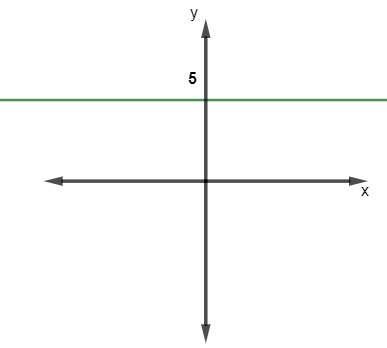
Vejamos agora o gráfico da função f(x) = 0, que está em cima do eixo x.

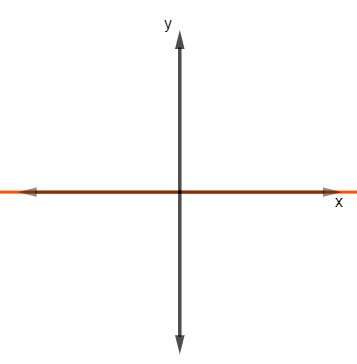
Agora, vejamos a representação gráfica da função f(x) =  \(-\) 2:

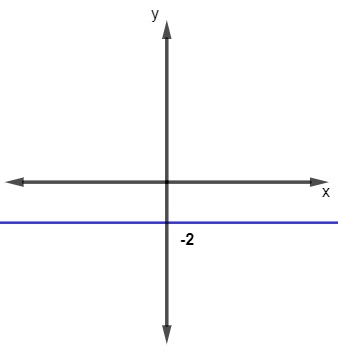
Leia também: Como construir o gráfico de uma função?

Exercícios resolvidos sobre função constante

Questão 1

Analise a lei de formação das funções a seguir:

\(f\left(x\right)=2x\)

\(g\left(x\right)=\frac{4}{\pi}\)

\(h\left(x\right)=\frac{x}{2}\)
Sabendo que as funções \(f,\ g\ e\ h\) são funções com domínio e contradomínio no conjunto dos números reais, marque a alternativa correta.

A) Somente a função \(f\left(x\right) \) é uma função constante.

B) Somente a função g(x) é uma função constante.

C) Somente a função h(x) é uma função constante.

D) Nenhuma das funções é constante.

E) Todas as funções são constantes.

Resolução:

Alternativa B

Podemos observar que somente a função g(x) é uma função constante, pois o número \(\frac{4}{\pi}\) é um número real.

Questão 2

(Vunesp) A representação gráfica de uma função constante com o maior domínio possível é uma

A) reta paralela ao eixo das ordenadas.

B) reta paralela ao eixo das abscissas.

C) reta não paralela ao eixo das abscissas, não paralela ao eixo das ordenadas e contendo o ponto (0, 0).

D) reta não paralela ao eixo das abscissas, não paralela ao eixo das ordenadas e não contendo o ponto (0, 0).

E) parábola, contendo o ponto (0, 0).

Resolução:

Alternativa B

O gráfico da função constante é uma reta paralela ao eixo x, que é o eixo das abscissas.

Por Raul Rodrigues de Oliveira
Professor de Matemática