Função logarítmica

A função logarítmica é aquela que possui em sua lei de formação o logaritmo de uma variável, ou seja, $f\left(x\right)=log_ax$. O domínio dessa função está no conjunto dos números reais positivos, sendo diferente de zero, e o contradomínio, no conjunto dos números reais. Vale salientar também que a base do logaritmo tem que ser necessariamente maior que 0 e diferente de 1.

O gráfico de uma função logarítmica pode ser crescente, quando a base for maior que 1, e decrescente, quando a base for menor que 1. Como o domínio é o conjunto dos números reais positivos e diferente de zero, o gráfico da função estará sempre nos 1º e 4º quadrantes do plano cartesiano.

Leia também: Função modular — aquela cuja lei de formação possui pelo menos uma variável dentro do módulo

Tópicos deste artigo

• 1 - Resumo sobre função logarítmica
• 2 - Videoaula sobre função logarítmica
• 3 - O que é função logarítmica?
• 4 - Domínio da função logarítmica
• 5 - Gráfico da função logarítmica
  • Função logarítmica crescente
  • Função logarítmica decrescente
• 6 - Função logarítmica e função exponencial
• 7 - Exercícios resolvidos sobre função logarítmica

Resumo sobre função logarítmica

• A função logarítmica é uma função $f:\mathbb{R}_+^\ast\rightarrow\mathbb{R}$ com lei de formação $f\left(x\right)=log_ax$.

• Se sua base é a > 1, então a função é crescente.

• Se sua base é $a<1$, então a função é decrescente.

• O gráfico da função logarítmica está sempre nos 1º e 4º quadrantes do plano cartesiano.

• A função logarítmica é a inversa da função exponencial.

Videoaula sobre função logarítmica

O que é função logarítmica?

Conhecemos como função logarítmica toda função ${f}:\mathbb{R}_+^\ast\rightarrow\mathbb{R}$ com lei de formação ${f}\left({x}\right)={lo}{g}_{a}{x}$. Em sua lei de formação, a base do logaritmo representada por a deve ser um número positivo diferente de 1.

Dada a lei de formação da função, temos:

$f\left(x\right)=log_ax$

• x →  variável independente

• $f\left(x\right)$ →  variável dependente

• a →  base do logaritmo

Vale relembrar a definição de logaritmo. O logaritmo b na base a, ou seja, $log_ab$, é igual ao expoente x que devemos elevar à base a que faz com que $a^x=b$.

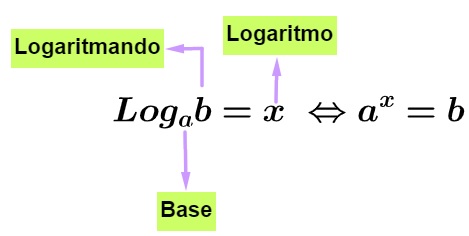
Temos como exemplo de função logarítmica:

• $f\left(x\right)=log_2x$

• $g\left(x\right)=log_\frac{1}{2}x$

• $h\left(x\right)=logx$

• $i\left(x\right)=log_{0,5}x$

Leia também: Função polinomial — a função que tem um polinômio em sua lei de formação

Domínio da função logarítmica

O domínio de uma relação entre dois conjuntos é importante para que essa relação seja classificada como uma função. A fim de que tenhamos de fato uma função logarítmica, é necessário que o domínio da função seja o conjunto dos números reais positivos e não nulos, ou seja, $D_f=\mathbb{R}_+^\ast$.

Em uma função, todo elemento do domínio deve ter necessariamente uma imagem no contradomínio. Supondo que x possa ser negativo, encontraremos alguns casos de indeterminação, como no exemplo a seguir:

$f\left(x\right)=log_3x$ se $x=-\ 3$

Não existe nenhum valor de b que faz com que $3^b=-3$, logo não há uma função, o que torna necessária essa restrição no domínio da função, fazendo com que a variável independente seja sempre um número real positivo diferente de zero.

Gráfico da função logarítmica

Na representação gráfica da função logarítmica, há dois tipos de comportamento possíveis: ou a função é crescente ou a função é decrescente. Devido às restrições existentes para o domínio da função logarítmica, o gráfico da função está localizado sempre nos 1º e 4º quadrantes. Vejamos, a seguir, representações gráficas de funções logarítmicas crescente e decrescente.

• Função logarítmica crescente

A função logarítmica é crescente quando à medida que o valor de x na função aumenta, o valor de f(x) também aumenta. Para que isso aconteça, é necessário que a base a da lei de formação $f\left(x\right)=log_ax$ seja maior que 1, ou seja, se a > 1 → f(x) é crescente.

Exemplo:

Faremos a representação gráfica da função a seguir:

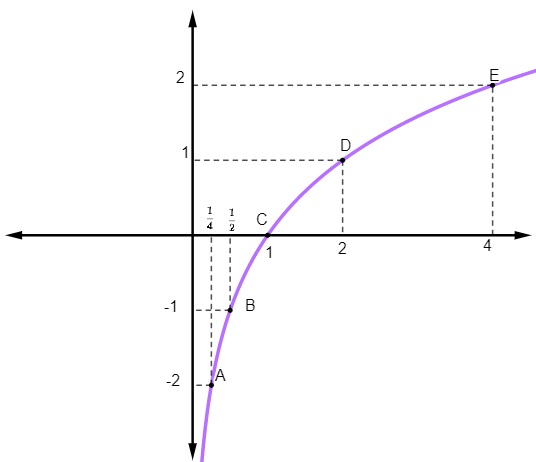
$f\left(x\right)=log_2x$

Para realizarmos a representação gráfica dessa função, calcularemos o seu valor numérico:

Como a sua base é 2, essa função é crescente, como mostra sua representação gráfica:

• Função logarítmica decrescente

Agora, faremos a representação gráfica de uma função decrescente.

Exemplo:

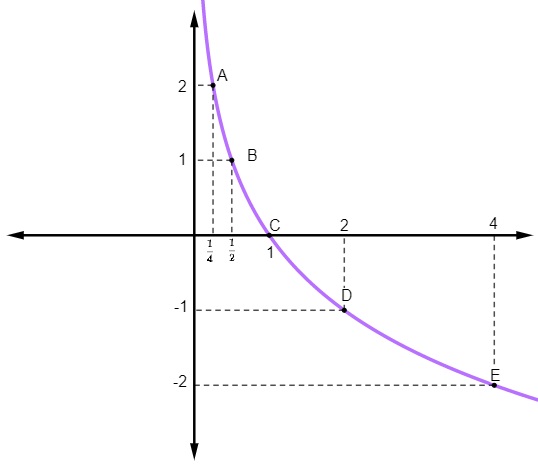
$f\left(x\right)=log_\frac{1}{2}x$

Calculando os valores numéricos:

Fazendo a representação gráfica:

Função logarítmica e função exponencial

O logaritmo é a operação inversa da potenciação. Sendo assim, a relação entre a função logarítmica e a função exponencial é que aquela é a função inversa desta, e vice-versa.

Considerando a função logarítmica $f\left(x\right)=log_ax$, se trocarmos $f\left(x\right)$ e $x$ de lugar, encontraremos a lei de formação da função inversa:

$x=log_af\left(x\right)$

$a^x=a^{log_af\left(x\right)}$

$a^x=f\left(x\right)$

Assim, a função inversa da função logarítmica é:

$f\left(x\right)=a^x$

Leia também: Diferenças entre domínio, contradomínio e imagem

Exercícios resolvidos sobre função logarítmica

Questão 1

Dadas as funções $f\left(x\right)=log_2x$ e $g\left(x\right)=log_\frac{1}{2}\ x$, o valor de $f\left(2\right)-g\left(2\right)$ é:

A) 0

B) 1

C) 2

D) 3

E) 4

Resolução:

Alternativa C

Calculando $f\left(2\right)=log_22$:

$2^y=2$

$y=1$

Logo, $f\left(2\right)=1$.

Agora, calcularemos $g\left(2\right)$:

$g\left(2\right)=log_\frac{1}{2}2$

$\left(\frac{1}{2}\right)^y=2$

$y=-\ 1\ $

$g\left(2\right)=-1$

Portanto:

$f\left(2\right)-g\left(2\right)=1-\left(-1\right)=1+1=2$

Questão 2

(UFPR) Suponha que o tempo necessário para se tomar uma decisão esteja relacionado com o número de escolhas de que se dispõe. Nesse caso, um modelo matemático que fornece o tempo de reação R, em segundos, em função do número de escolhas N é dado pela expressão:

R = 0,17 + 0,44 log(N)

De acordo com esse modelo, quando o número de escolhas for reduzido de 100 para 10, qual será o percentual de diminuição no tempo de reação, aproximadamente?

A) 26%

B) 42%

C) 55%

D) 88%

Resolução:

Alternativa B

Primeiramente, calcularemos N = 100:

$R=0,17+0,44\ log\ 100$

$R=0,17+0,44\cdot2\ $

$R=0,17+0,88\ $

$R=1,05\ $

Agora, calcularemos N = 10:

$R=0,17+0,44\ log\ 10$

$R=0,17+0,44\cdot1$

$R=0,17+0,44$

$R=0,61$

Assim, o tempo de reação reduziu de 105 para 0,61.

$105-0,61=0,44$

Ao realizar a divisão de 44 por 105 para encontrar a porcentagem de redução, temos:

$44∶105\approx0,42=42%$ de redução

 

Por Raul Rodrigues de Oliveira
Professor de Matemática