Funções periódicas

As funções periódicas são aquelas nas quais os valores da função (f(x) = y) se repetem para determinados valores da variável x, ou seja, para cada período determinado pelos valores de x, iremos obter valores repetidos para a função.

Vejamos um exemplo para melhor compreender essa definição:

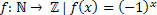
Façamos uma tabela com alguns valores para a variável x, relacionando o valor da função para cada valor de x.

Note que f(x)= 1 ocorre somente quando o valor da variável x é par.
Note que f(x)= –1 ocorre somente quando o valor da variável x é impar.

Ou seja, esta é uma função periódica, na qual temos dois períodos diferentes, um no qual o valor da função é 1 (f(x)= 1) e outro no qual a função é –1 (f(x)= –1).

Note também que quando x varia duas unidades, o valor da função se repete, ou seja: f(x)= f(x+2)= f(x+4)= f(x+6)... Dessa forma, podemos afirmar que o período dessa função é 2.

Sendo assim, podemos definir as funções periódicas da seguinte maneira:

“Uma função é denominada periódica caso exista um número real p > 0, tal que: f(x)=f(x+p). Com isso, o menor valor de p, que satisfaça essa igualdade, é chamado de período da função f”.

Sendo assim, caso ocorra: f(x)= f(x+1,5)= f(x+3)= f(x+4,5), trata-se de uma função periódica cujo período p = 1,5.

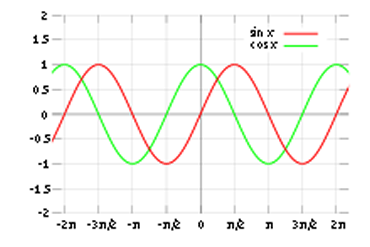
Nas funções trigonométricas, temos exemplos de funções periódicas como, por exemplo, a função seno, função cosseno, função tangente.

Exemplo:

y = cos x

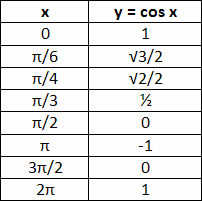
Veja que o valor 1 se repete em um período p = 2π, e que o valor y = 0 se repete em um período p = π.

Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola