Função raiz é a função que possui pelo menos uma variável dentro de um radical. Ela é chamada também de função irracional, sendo a mais comum delas a raiz quadrada, porém existem outras, como a função raiz cúbica, entre outros índices possíveis.
Para encontrar o domínio de uma função raiz, é importante analisar o índice. Quando o índice é par, o radicando deve ser positivo por condição de existência da raiz. Já o contradomínio da função raiz é o conjunto dos números reais. Também é possível fazer a representação gráfica de uma função raiz.
Saiba mais: Domínio, contradomínio e imagem — o que cada um representa?
Tópicos deste artigo
- 1 - Resumo sobre função raiz
- 2 - O que é a função raiz?
- 3 - Como calcular a função raiz
- 4 - Domínio e contradomínio de uma função raiz
- 5 - Gráfico de uma função raiz
- 6 - Exercícios resolvidos sobre função raiz
Resumo sobre função raiz
-
A função raiz é aquela que possui uma variável dentro do radical.
-
Para encontrar o domínio da função raiz, é necessário analisar o índice do radical.
-
Se o índice da raiz for par, no radicando só haverá valores reais positivos.
-
Se o índice da raiz for ímpar, o domínio será os números reais.
-
-
A função raiz quadrada é a mais comum entre as funções raiz.
Anuncie aqui -
A função raiz quadrada possui gráfico sempre crescente e positivo.
O que é a função raiz?
Classificamos qualquer função que possua uma variável dentro do radical como função raiz. De forma análoga, podemos considerar como função raiz aquela que possui uma variável elevada a um expoente igual a uma fração própria, que são frações que possuem o numerador menor que o denominador, pois sempre que necessário podemos transformar um radical em uma potência com expoente fracionário.
-
Exemplos de função raiz:
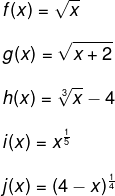
Como calcular a função raiz
Conhecendo a lei de formação de uma função raiz, deve-se calcular o valor numérico da função. Assim como em todas as funções que estudamos, calculamos o valor numérico da função substituindo a variável pelo valor desejado.
-
Exemplo de como calcular a função raiz:
Dada a função f(x) = 1 + √x, encontre o valor de:
a) f(4)
Substituindo x = 4, temos:
f(4) = 1 + √4
f(4) = 1 + 2
f(4) = 5
Essas funções são conhecidas como irracionais pelo fato de que a maioria das suas imagens são números irracionais. Por exemplo, se calcularmos f(2), f(3) para essa mesma função:
b) f(2) = 1 + √2
c) f(3) = 1 + √3
Deixamos representado dessa forma, como uma adição entre 1 e o número irracional. Entretanto, quando necessário, podemos utilizar uma aproximação para essas raízes não exatas.
Veja também: Função inversa — o tipo de função que faz exatamente o inverso da função f(x)
Domínio e contradomínio de uma função raiz
Quando estudamos uma função raiz, é fundamental analisar caso a caso, para que seja possível definir bem o seu domínio. O domínio depende diretamente do índice da raiz e do que está em seu radicando. Já o contradomínio de uma função raiz é sempre o conjunto dos números reais.
Vejamos a seguir alguns exemplos:
-
Exemplo 1:
Começando pela função raiz mais comum e mais simples, a seguinte função:
f(x) = √x
Analisando o contexto, nota-se que, como se trata de uma função quadrada e o contradomínio é o conjunto dos números reais, não existe no conjunto raiz negativa quando o índice for par. Sendo assim, o domínio da função é o conjunto dos números reais positivos, ou seja:
D = R+
-
Exemplo 2:
![]()
Como há uma raiz quadrada, para que essa função exista no conjunto dos números reais, o radicando deve ser maior ou igual a zero. Então, calculamos:
x – 4 ≥ 0
x ≥ 4
Assim, o domínio da função é:
D = {x ∈ R | x ≥ 4}
-
Exemplo 3:
![]()
Nessa função não há restrição, pois o índice da raiz é ímpar, portanto o radicando pode ser negativo. Dessa forma, o domínio dessa função será os números reais:
D = R
Acesse também: Radiciação — a operação numérica inversa à potenciação
Gráfico de uma função raiz
Na função raiz quadrada de x, o gráfico é sempre positivo. Em outras palavras, a imagem da função é sempre um número real positivo, os valores que x pode assumir são sempre positivos e o gráfico é sempre crescente.
-
Exemplo de função raiz quadrada:
Vejamos a representação do gráfico da função raiz quadrada de x.
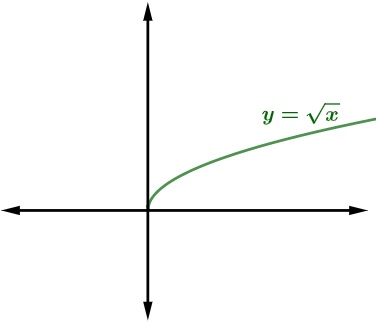
-
Exemplo de função raiz cúbica:
Agora, faremos a representação do gráfico de uma função com índice ímpar. É possível fazer a representação de outras funções raiz, como as funções cúbicas. Vejamos, a seguir, a representação da função raiz cúbica de x. Note que, nesse caso, como a raiz possui índice ímpar, x pode admitir valores negativos, e a imagem também pode ser negativa.
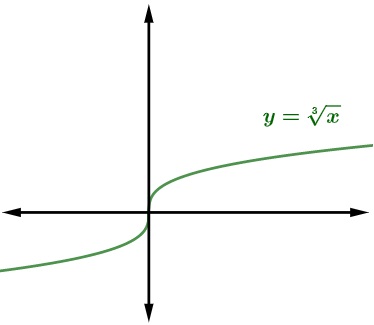
Leia também: Como construir o gráfico de uma função?
Exercícios resolvidos sobre função raiz
Questão 1
Dada a função raiz a seguir, com domínio no conjunto dos números reais positivos e contradomínio no conjunto dos números reais, qual deve ser o valor de x para que f(x) = 13?
![]()
A) 3
B) 4
C) 5
D) 6
E) 7
Resolução:
Alternativa C
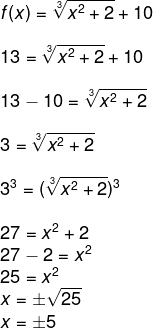
Como o domínio da função é o conjunto dos números reais positivos, o valor que faz com que f(x) seja igual a 13 é x = 5.
Questão 2
Sobre a função f(x), julgue as afirmativas a seguir.
![]()
I → O domínio dessa função é o conjunto dos números reais maiores que 5.
II → Nessa função, f(1) = 2.
III → Nessa função, f( – 4) = 3.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Resolução:
Alternativa A
I → Falsa
Sabemos que 5 – x > 0, então temos:
– x > – 5 ( – 1)
x < 5
O domínio é, portanto, os números reais menores que 5.
II → Verdadeira
Calculando f(1), temos:
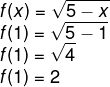
III → Verdadeira
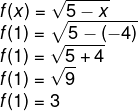
Por Raul Rodrigues de Oliveira
Professor de Matemática

