Função do 2º grau ou função quadrática

A função do 2º grau ou função quadrática é uma função de domínio real, ou seja, qualquer número real pode ser o x e, a cada número real x, associamos um número da forma ax² + bx + c.

Em outras palavras, a função quadrática f é definida por:

Veremos, a seguir, como calcular esse tipo de função, relembrando a fórmula de Bhaskara para encontrar as raízes da função, além de conhecermos o seu tipo de gráfico, seus elementos e como desenhá-lo com base na interpretação dos dados obtidos pela solução.

Tópicos deste artigo

• 1 - O que é uma função do 2º grau?
• 2 - Gráfico da função quadrática
• 3 - Raízes da função quadrática
• 4 - Exercícios resolvidos

O que é uma função do 2º grau?

Uma função f: R à → é chamada de função do 2º grau ou função quadrática quando existir a, b, c € R com a ≠ 0, de maneira que f(x) = ax² + bx + c, para todo x € R.

Exemplos:

• f(x) = 6x² - 4x + 5 → a = 6; b = -4; c = 5.
• f(x) = x² - 9 → a = 1; b = 0; c = -9.
• f(x) = 3x² +3x → a = 3 ; b = 3 ; c = 0.
• f(x) = x² – x → a = 1; b = -1; c = 0.

Para cada número real x, devemos substituir e realizar as devidas operações para encontrar sua imagem. Veja o exemplo a seguir:

Vamos determinar a imagem do número real -2 da função f(x) = 6x² - 4x + 5. Para isso, basta substituir o número real dado na função, assim:

f (-2) = 6(-2)² – 4(-2) +5

f (-2) = 6(4) + 8 +5

f (-2) = 24 + 8 + 5

f (-2) = 37

Logo, a imagem do número -2 é 27, resultando no par ordenado (-2; 37).

Leia também: Equação do 2º grau: a equação que possui incógnita de expoente 2

Gráfico da função quadrática

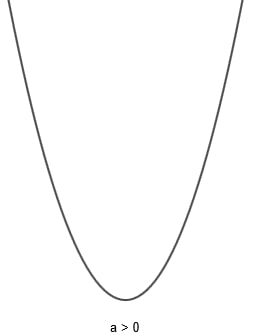
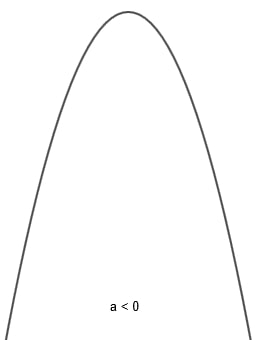
Ao esboçar o gráfico da função quadrática, encontramos uma curva, que vamos chamar de parábola. Sua concavidade depende do coeficiente a da função f. Quando a função tiver o coeficiente a maior que 0, a parábola terá a concavidade para cima; quando o coeficiente a for menor que 0, a parábola terá a concavidade para baixo.

Raízes da função quadrática

As raízes de uma função quadrática fornecem os pontos de intersecção do gráfico da função com os eixos do plano cartesiano. Quando consideramos uma função quadrática da forma y = ax² + bx + c e tomamos inicialmente o x = 0, vamos encontrar a intersecção com o eixo O_Y. Agora, se tomamos o y = 0, vamos encontrar a intersecção com eixo O_X, ou seja, as raízes da equação fornecem a intersecção com o eixo X. Veja um exemplo:

a) y = x² – 4x

Vamos tomar x = 0 e substituir na função dada. Assim, y = 0² – 4 (0) = 0. Note que, quando x = 0, temos y = 0. Assim, temos o seguinte par ordenado (0, 0). Esse par ordenado fornece a intersecção com o eixo y. Agora, tomando y = 0 e substituindo na função, vamos obter o seguinte:

x² – 4x = 0

x.(x - 4) = 0

x’ = 0

x’’- 4 = 0

x’’ = 4

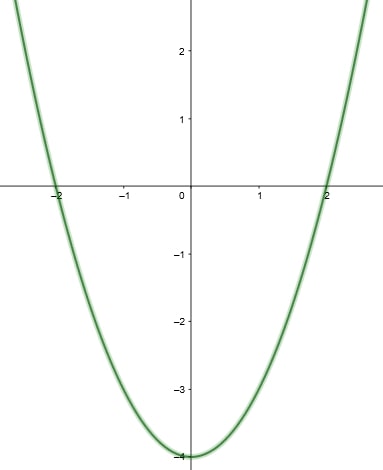
Logo, temos dois pontos de intersecção (0, 0) e (4, 0) e, no plano cartesiano, temos o seguinte:

Perceba que podemos usar a relação de Bhaskara para encontrar os zeros da função. Com isso, ganhamos uma ferramenta muito importante: olhando para o discriminante, podemos saber em quantos lugares o gráfico intercepta o eixo X.

• Se o delta é maior que zero (positivo), o gráfico “corta” o eixo x em dois pontos, ou seja, temos x’ e x’’.
• Se o delta é igual a zero, o gráfico “corta” o eixo x em um ponto, ou seja, x’ = x’’.
• Se o delta é menor que zero (negativo), o gráfico não “corta” o eixo x, pois não existem raízes.

Exercícios resolvidos

Questão 1 - Dada a função f(x) = -x² + 2x – 4. Determine:

a) A intersecção com o eixo O_Y.

b) A intersecção com o eixo O_X.

c) Esboce o gráfico da função.

Solução:

a) Para determinar a intersecção com eixo O_Y , basta tomar o valor de x =

b) 0. -(0)² +2(0) – 4

0 + 0 – 4

-4

Assim, temos o par ordenado (0, -4).

c) Para encontrar a intersecção com o eixo O_X, basta tomar o valor de y = 0. Assim:

-x² +2x – 4 = 0

Utilizando o método de Bhaskara, temos que:

Δ = b² - 4ac

Δ = (2)² - 4(-1)(-4)

Δ = 4 - 16

Δ = -12

Como o valor do discriminante é menor que zero, a função não intercepta o eixo X.

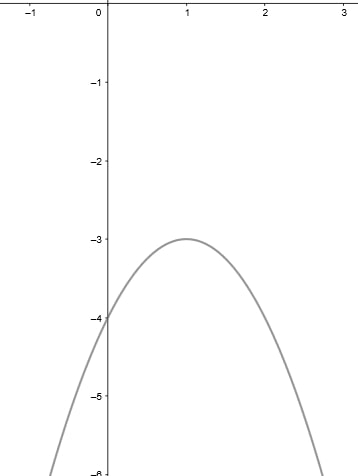
d) Para fazer o esboço do gráfico, devemos olhar os pontos de intersecção e analisar a concavidade da parábola. Como a < 0, a parábola será côncava para baixo. Assim:

 

Por Robson Luiz
Professor de Matemática