Função injetora

 A função injetora, conhecida também como função injetiva, é um caso particular de função. Para que uma função seja considerada injetora, temos que ter a seguinte ocorrência: dados dois elementos, x₁ e x_2, pertencentes ao conjunto do domínio, com x₁ diferente de x₂, as imagens f(x₁) e f(x₂) são sempre distintas, ou seja, f(x₁) ≠ f(x₂). Essa função possui características específicas que possibilitam a identificação do seu gráfico e também a análise da lei de formação.

Leia também: Domínio, contradomínio e imagem – termos básicos para compreensão do conteúdo de funções

Tópicos deste artigo

• 1 - O que é função injetora?
• 2 - Como calcular uma função injetora?
• 3 - Gráfico de funções injetoras
• 4 - Exercícios resolvidos

O que é função injetora?

Para construir alguns exemplos de função injetora, é importante compreender a definição desse tipo de função. Uma função f: A → B é classificada como injetora se, e somente se, elementos diferentes do conjunto A possuem imagens diferentes no conjunto B, ou seja:

Exemplo 1:

Veja a seguir um exemplo de função injetora no diagrama de Venn:

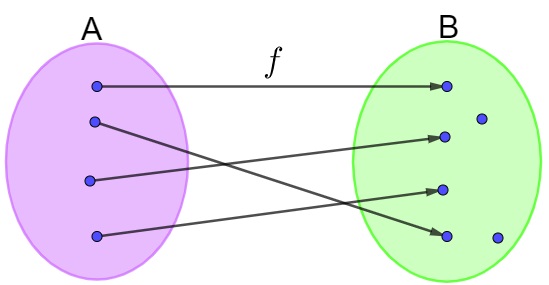
Exemplo 2:

Veja a seguir um exemplo de função não injetora. Note que, no conjunto A, existem dois elementos distintos que possuem a mesma imagem no conjunto B, o que contradiz a definição de função injetora.

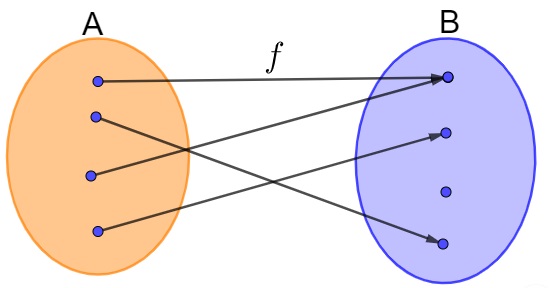
Como calcular uma função injetora?

Para verificar se uma função é injetora ou não, é necessário analisar o comportamento da lei de formação e também o domínio e o contradomínio em que a função está definida.

Exemplo:

Dada a função f: R → R, com a lei de formação f(x) = 2x, verifique se ela é injetora.

Pela lei de formação, podemos observar que ela pega um número real do domínio e o transforma em seu dobro. Dois números reais distintos, ao serem multiplicados por dois, geram resultados distintos. A função f, como podemos observar, é uma função injetora, pois, para quaisquer dois valores de x₁ e x₂, o valor de f(x₁) ≠ f(x₂).

Exemplo 2:

Dada a função f: R → R, com lei de formação f(x) = x², verifique se ela é injetora.

Podemos observar que, para esse domínio, essa função não é injetora, pois temos que a imagem de um número qualquer é igual à imagem do seu oposto, por exemplo:

f( 2) = 2² = 4
f( -2 ) = (– 2) ² = 4

Note que f(2) = f ( – 2), o que contradiz a definição de uma função injetora.

Exemplo 3:

Dada a função f: R⁺ → R, com lei de formação f(x) = x², verifique se ela é injetora.

Note que agora o domínio são os números reais positivos e o zero. A função transforma o número real em seu quadrado; nesse caso, quando o domínio é o conjunto dos números reais positivos, essa função é injetora, pois o quadrado de dois números positivos distintos sempre vai gerar resultados distintos. Então, é muito importante lembrar que, além da lei de formação da função, precisamos analisar o seu domínio e contradomínio.

Leia também: O que é uma função inversa?

Gráfico de funções injetoras

Para identificar se o gráfico é de uma função injetora ou não, basta checar se existem dois valores de x distintos que geram o mesmo correspondente em y, ou seja, verificar a validade da definição de função injetora.

No intervalo em que vamos observar o gráfico, a função tem que ser exclusivamente crescente ou exclusivamente decrescente. Gráficos como a parábola ou o da função seno não são gráficos de funções injetoras.

Exemplo 1:

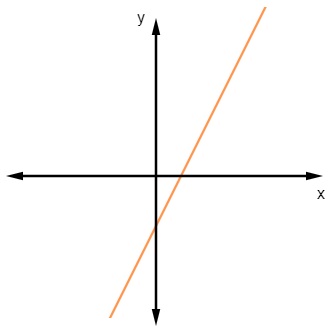
A reta crescente é o gráfico de uma função injetora. Perceba que ele é sempre crescente e que não existe valor de y que tenha dois correspondentes distintos.

Exemplo 2:

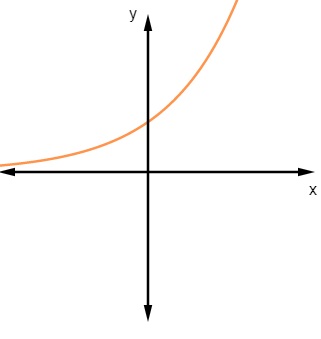
O gráfico de uma função exponencial também é o gráfico de uma função injetora.

Exemplo 3:

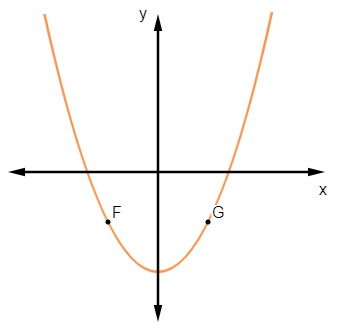
O gráfico de uma função quadrática é sempre uma parábola. Quando o domínio envolve os números reais, é possível perceber que existem valores de x distintos que têm o mesmo correspondente em y, como nos pontos F e G, o que faz com que esse gráfico seja de uma função que não é injetora.

Em resumo, para saber se o gráfico é ou não de uma função injetora, basta checar se a definição de função injetora vale ou não para essa função.

Exercícios resolvidos

Questão 1 – (Enem 2017 – PPL) No primeiro ano do ensino médio de uma escola, é hábito os alunos dançarem quadrilha na festa junina. Neste ano, há 12 meninas e 13 meninos na turma, e para a quadrilha foram formados 12 pares distintos, compostos por uma menina e um menino. Considere que as meninas sejam os elementos que compõem o conjunto A e os meninos, o conjunto B, de modo que os pares formados representem uma função f de A em B.

Com base nessas informações, a classificação do tipo de função que está presente nessa relação é

A) f é injetora, pois para cada menina pertencente ao conjunto A está associado um menino diferente pertencente ao conjunto B.

B) f é sobrejetora, pois cada par é formado por uma menina pertencente ao conjunto A e um menino pertencente ao conjunto B, sobrando um menino sem formar par.

C) f é injetora, pois duas meninas quaisquer pertencentes ao conjunto A formam par com um mesmo menino pertencente ao conjunto B, para envolver a totalidade de alunos da turma.

D) f é bijetora, pois dois meninos quaisquer pertencentes ao conjunto B formam par com uma mesma menina pertencente ao conjunto A.

E) f é sobrejetora, pois basta que uma menina do conjunto A forme par com dois meninos pertencentes ao conjunto B, assim nenhum menino ficará sem par.

Resolução

Alternativa A.

Essa função é injetora, pois, para cada elemento do conjunto A, existe um único correspondente no conjunto B. Note que não há a possibilidade de duas meninas dançarem com o mesmo par, logo essa relação é injetora.

Questão 2 – (IME - RJ) Considere os conjuntos A = {(1,2), (1,3), (2,3)} e B = {1, 2, 3, 4, 5}, e seja a função f: A → B tal que f (x,y) = x + y.

É possível afirmar que f é uma função:

A) injetora.

B) sobrejetora.

C) bijetora.

D) par.

E) ímpar.

Resolução

Alternativa A.

Analisando o domínio, temos que:

f(1,2) = 1 + 2 = 3
f(1,3) = 1 + 3 = 4
f(2,3) = 2 + 3 = 5

Note que, para quaisquer dois termos distintos do domínio, eles estão relacionados a termos distintos no contradomínio, o que torna essa função injetora. 

Por Raul Rodrigues de Oliveira
Professor de Matemática