Conjuntos

A compreensão de conjuntos é a principal base para o estudo da álgebra e de conceitos de grande importância na Matemática, como funções e inequações. A notação que usamos para conjuntos é sempre uma letra maiúscula do nosso alfabeto (por exemplo, conjunto A ou conjunto B).

Em se tratando da representação dos conjuntos, ela pode ser feita pelo diagrama de Venn, pela simples descrição das características dos seus elementos, pela enumeração dos elementos ou pela descrição das suas propriedades. Ao trabalhar com problemas que envolvem conjuntos, existem situações que exigem a realização de operações entre os conjuntos, sendo elas a união, a intersecção e a diferença. Vamos estudar tudo isso detalhadamente?

Veja também: Expressões numéricas – aprenda a resolvê-las!

Tópicos deste artigo

• 1 - Notação e representação de conjuntos
• 2 - Elementos de um conjunto e relação de pertinência
• 3 - Igualdade de conjuntos
• 4 - Relação de inclusão
• 5 - Subconjuntos
• 6 - Conjunto unitário
• 7 - Conjunto vazio
• 8 - Conjuntos das partes
  • Formas de representação dos conjuntos
• 9 - Conjunto finito e infinito
• 10 - Conjunto universo
• 11 - Operações com conjuntos
  • União
• 12 - Leis de Morgan
• 13 - Exercícios resolvidos

Notação e representação de conjuntos

Para representação de um conjunto, utilizamos sempre uma letra maiúscula do alfabeto, e os elementos estão sempre entre chaves e são separados por vírgula. Para representar o conjunto dos números pares maiores que 1 e menores que 20, por exemplo, usamos a seguinte notação: P ={2,4,6,8,10,12,14,16,18}.

• Formas de representação dos conjuntos

1. Representação por enumeração: podemos enumerar seus elementos, ou seja, fazer uma lista, sempre entre chaves. Veja um exemplo:

A = {1,5,9,12,14,20}

2. Descrevendo as características: podemos simplesmente descrever a característica do conjunto. Por exemplo, seja X um conjunto, temos que X = {x é um número positivo múltiplo de 5}; Y: é o conjunto dos meses do ano.

3. Diagrama de Venn: os conjuntos também podem ser representados na forma de um diagrama, conhecido como diagrama de Venn, que é uma representação mais eficiente para a realização das operações.

Exemplo:

Dado o conjunto A = {1,2,3,4,5}, podemos representá-lo no diagrama de Venn a seguir:

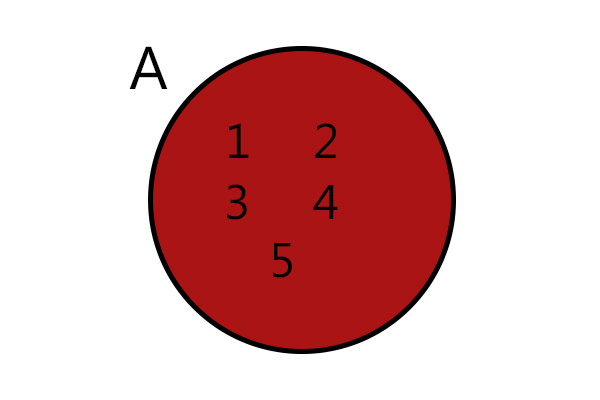
Elementos de um conjunto e relação de pertinência

Dado um elemento qualquer, podemos dizer que o elemento pertence ao conjunto ou não pertente a esse conjunto. Para representar essa relação de pertinência de forma mais rápida, utilizamos os símbolos  ​​ (lê-se pertence) e ∉ (lê-se não pertente). Por exemplo, seja P o conjunto dos números pares, podemos dizer que o 7 ∉ P e que 12  P.

Igualdade de conjuntos

É inevitável a comparação entre os conjuntos, sendo assim, podemos afirmar que dois conjuntos são iguais ou não verificando cada um dos seus elementos. Seja A = { 0,1,3,4,8} e B = { 8,4,3,1,0}, ainda que os elementos estejam em ordem diferente, podemos afirmar que os conjuntos A e B são iguais: A = B.

Relação de inclusão

Ao comparar dois conjuntos, podemos nos deparar com diversas relações, e uma delas é a relação de inclusão. Para essa relação, precisamos conhecer alguns símbolos:

⊃ → contém ⊂ → está contido

⊅ → não contém ⊄ → não está contido

Quando todos os elementos de um conjunto A pertencem também a um conjunto B, dizemos que A ⊂ B ou que A está contido em B. Por exemplo, A= {1,2,3} e B={1,2,3,4,5,6}. É possível também fazer a representação pelo diagrama de Venn, que ficaria assim:

• A está contido em B:

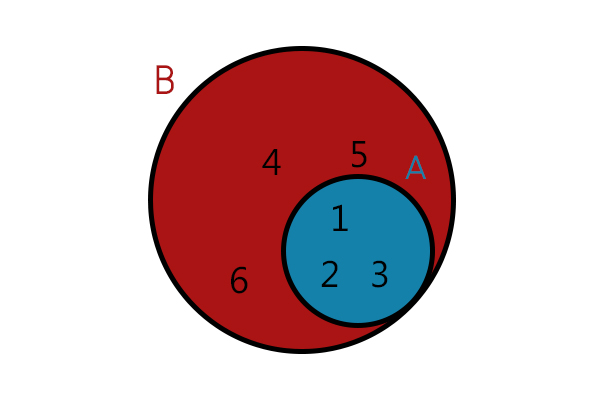
A ⊂ B

Subconjuntos

Quando acontece uma relação de inclusão, ou seja, o conjunto A está contido no conjunto B, podemos dizemos que A é subconjunto de B. O subconjunto continua sendo um conjunto, e um conjunto pode ter vários subconjuntos, construídos a partir dos elementos pertencentes a ele.

Por exemplo: A: {1,2,3,4,5,6,7,8} tem como subconjuntos os conjuntos B: {1,2,3}; C: {1,3,5,7}; D: {1} e, até mesmo, o conjunto A {1,2,3,4,5,6,7,8}, ou seja, A é subconjunto dele mesmo.

Conjunto unitário

Como o nome já sugere, é aquele conjunto que possui somente um elemento, como o conjunto D: {1} mostrado anteriormente. Dado o conjunto B: {1,2,3}, temos os subconjuntos {1}, {2} e {3}, que são todos conjuntos unitários.

ATENÇÃO: O conjunto E: {0} também é um conjunto unitário, pois ele possui um único elemento, o “0”, não se tratando de um conjunto vazio.

Leia também: Conjunto dos números inteiros – elementos e características

Conjunto vazio

Com um nome mais sugestivo ainda, o conjunto vazio não possui nenhum elemento e é subconjunto de qualquer conjunto. Para representar o conjunto vazio, há duas representações possíveis, sendo elas V: { } ou o símbolo Ø.

Conjuntos das partes

Conhecemos como conjuntos das partes todos os subconjuntos possíveis de um determinado conjunto. Seja A: {1,2,3,4}, podemos listar todos os subconjuntos desse conjunto A começando com os conjuntos que possuem nenhum elemento (vazios) e, depois, os que possuem um, dois, três e quatro elementos, respectivamente.

• Conjunto vazio: { };

• Conjuntos unitários: {1}; {2};{3}; {4}.

• Conjuntos com dois elementos: {1,2}; {1,3}; {1,4}; {2,3}; {2,4}; {3,4}.

• Conjuntos com três elementos: {1,2,3}; {1,3,4}; {1,2,4}; {2,3,4}.

• Conjunto com quatro elementos: {1,2,3,4}.

Sendo assim, podemos descrever o conjunto das partes de A desta forma:

P: { { }, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,3,4}, {1,2,4}, {2,3,4}, {1,2,3,4} }

Para saber a quantidade de partes em que é possível dividir um conjunto, usamos a fórmula:

n[ P(A)] = 2ⁿ

O número de partes de A é calculado por uma potência de base 2 elevada a n, em que n é a quantidade de elementos do conjunto.

Considere o conjunto A: {1,2,3,4}, que possui quatro elementos. O total de subconjuntos possíveis desse conjunto é 2⁴ =16.

Leia também: O que é o conjunto dos números irracionais?

Conjunto finito e infinito

Ao trabalhar com conjuntos, encontramos conjuntos que são limitados (finitos) e aqueles que são ilimitados (infinitos). O conjunto dos números pares ou ímpares, por exemplo, é infinito e, para representá-lo, descrevemos alguns dos seus elementos em sequência, de forma que seja possível prever quais serão os próximos elementos, e colocamos reticências no final.

I: {1,3,5,7,9,11...}

P: {2,4,6,8,10, ...}

Já em um conjunto finito, não colocamos as reticências no final, pois ele possui começo e final definidos.

A: {1,2,3,4}.

Conjunto universo

O conjunto universo, denotado por U, é definido como o conjunto formado por todos os elementos que devem ser considerados dentro de um problema. Todo elemento pertence ao conjunto universo e todo conjunto está contido no conjunto universo.

Operações com conjuntos

As operações com conjuntos são: união, intersecção e diferença.

• Intersecção de conjuntos

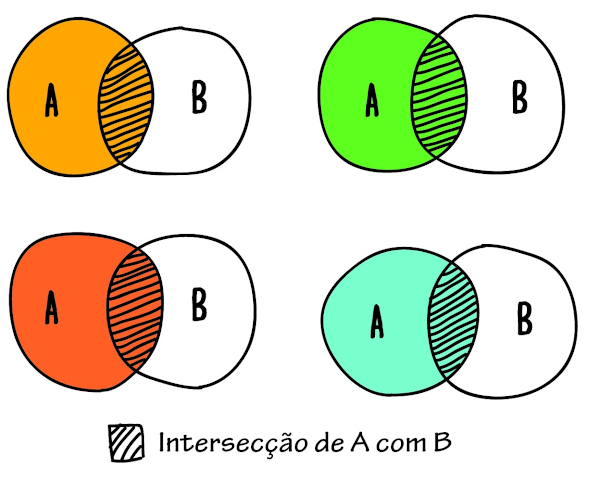
Ocorre uma intersecção quando os elementos pertencem simultaneamente a um ou mais conjuntos. Ao escrever A∩B, estamos procurando os elementos que pertencem tanto ao conjunto A quanto ao conjunto B.

Exemplo:

Considere A= {1,2,3,4,5,6} e B = {2,4,6,7,8}, os elementos que pertencem tanto ao conjunto A quanto ao conjunto B são: A∩B = {2,4,6}. A representação dessa operação é feita da seguinte forma:

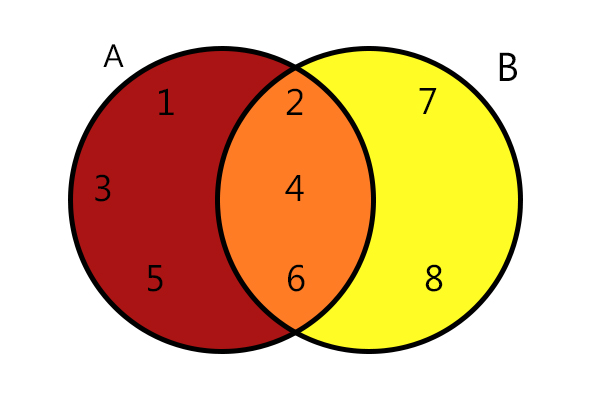
­­ A∩B

Quando os conjuntos não possuem nenhum elemento em comum, são conhecidos como conjuntos disjuntos.

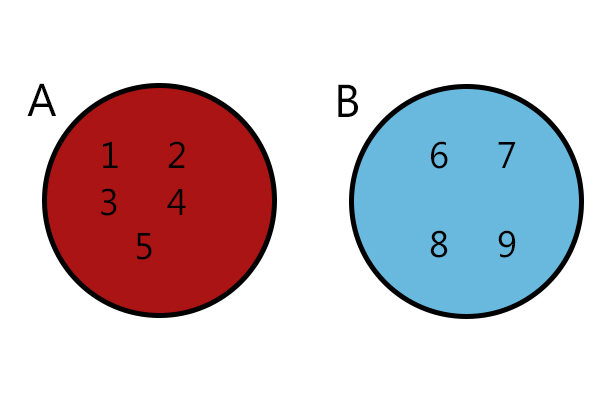
A∩B = Ø

 

• Diferença entre conjuntos

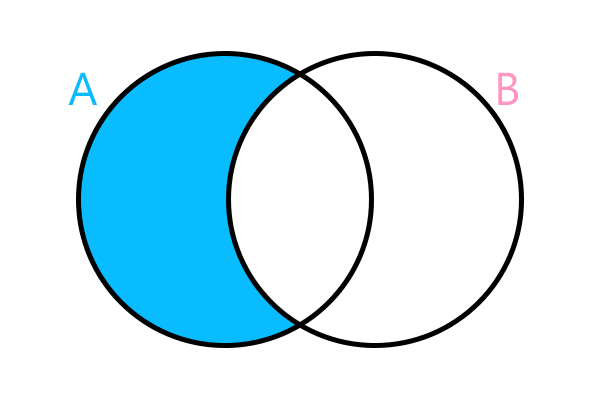
Calcular a diferença entre dois conjuntos é procurar os elementos que pertencem a somente um dos dois conjuntos. Por exemplo, A – B tem como resposta um conjunto composto por elementos que pertencem ao conjunto A e não pertencem ao conjunto B.

Exemplo: A: {1,2,3,4,5,6} e B: {2,4,6,7,8}. Note que A ∩ B ={2,4,6}, então temos que:

a) A – B = { 1,3,5 }

b) B – A = { 7,8 }

• União

A união de dois ou mais conjuntos é a junção dos seus termos. Caso haja elementos que se repitam nos dois conjuntos, eles são escritos uma única vez. Por exemplo: A={1,2,3,4,5} e B={4,5,6,7,10,14}. Para representar a união, usamos o símbolo (lê-se: A união com B).

A U B = {1,2,3,4,5,6,7,10,14}

Para saber mais detalhes sobre essas operações e conferir vários exercícios resolvidos, leia: Operações com conjuntos.

Leis de Morgan

Sejam A e B dois conjuntos e seja U o conjunto universo, existem duas propriedades que são dadas pelas Leis de Morgan, sendo elas:

(A U B)^c = A^c ∩ B^c

(A ∩ B)^c = A^c U B^c

Exemplo:

Dados os conjuntos:

• U: {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}

• A: {2,4,6,8,10,12,14,16,18,20}

• B: {5,10,15,20}

Vamos verificar que (A U B)^c = A^c ∩ B^c . Assim, temos que:

A U B = {2,4,5,6,8,10,12,14,15,16,18,20}

Logo, (A U B)^c={1,3,7,9,11,13,17,19}

Para verificar a veracidade da igualdade, vamos analisar a operação A^c ∩ B^c:

A^c:{1,3,5,7,9,11,13,15,17,19}

B^c:{1,2,3,4,6,7,8,9,11,12,13,14,16,17,18,19}

Então, A^c ∩ B^c ={1,3,7,9,11,13,15,17,19}.

(A U B)^c = A^c ∩ B^c

Exercícios resolvidos

01) Considere U: {1,2,3,4,5,6,7,8,9,10}, A: {1,2,3,4,5,6} e B: {4,5,6,7,8,9}. Mostre que (A ∩ B)^c = A^c U B^c.

Resolução:

• 1º passo: encontrar (A ∩ B)^c. Para isso, temos que A ∩ B = {4,5,6} , então (A ∩ B)^c ={1,2,3,7,8,9,10}.

• 2º passo: encontrar A^c U B^c. A^c:{7,8,9,10} e B^c:{1,2,3,10}, então A^c U B^c = {1,2,3,7,8,9,19}.

Fica demonstrado que (A ∩ B)^c = A^c U B^c.

02) Sabendo que A é o conjunto dos números pares de 1 até 20, qual é a quantidade total de subconjuntos que podemos construir a partir dos elementos desse conjunto?

Resolução:

Seja P o conjunto descrito, temos que P: {2,4,6,8,10,12,14,16,18,20}. Sendo assim, o número de elementos de P é 10.

Pela teoria do conjunto das partes, o número de subconjuntos possíveis de P é:

2¹⁰=1024

 

Por Raul Rodrigues de Oliveira
Professor de Matemática