Exemplo 1
Após o início de um experimento o número de bactérias de uma cultura é dado pela expressão:
N(t) = 1200*20,4t
Quanto tempo após o início do experimento a cultura terá 19200 bactérias?
N(t) = 1200*20,4t
N(t) = 19200
1200*20,4t = 19200
20,4t = 19200/1200
20,4t = 16
20,4t = 24
0,4t = 4
t = 4/0,4
t = 10 h
A cultura terá 19200 bactérias após 10 h.
Exemplo 2
A quantia de R$ 1200,00 foi aplicada durante 6 anos em uma instituição bancária a uma taxa de 1,5% ao mês, no sistema de juros compostos.
a) Qual será o saldo no final de 12 meses?
b) Qual será o montante final?
M = C(1+i)t (Fórmula dos juros compostos) onde:
C = capital
M = montante final
i = taxa unitária
t = tempo de aplicação
a) Após 12 meses.
Resolução
M = ?
C = 1200
i = 1,5% = 0,015 (taxa unitária)
t = 12 meses
M = 1200(1+0,015)12
M = 1200(1,015) 12
M = 1200*(1,195618)
M = 1.434,74
Após 12 meses ele terá um saldo de R$ 1.434,74.
b) Montante final
Resolução
M = ?
C = 1200
i = 1,5% = 0,015 (taxa unitária)
t = 6 anos = 72 meses
M = 1200(1+ 0,015)72
M = 1200(1,015) 72
M = 1200(2,921158)
M = 3.505,39
Após 6 anos ele terá um saldo de R$ 3.505,39
Exemplo 3
Sob certas condições, o número de bactérias B de uma cultura , em função do temo t, medido em horas, é dado por B(t) = 2t/12. Qual será o número de bactérias 6 dias após a hora zero?
6 dias = 6 * 24 = 144 horas
B(t) = 2t/12
B(144) = 2144/12
B(144) = 212
B(144) = 4096 bactérias
A cultura terá 4096 bactérias.
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

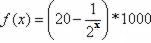 . Determine a população referente ao terceiro ano.
. Determine a população referente ao terceiro ano.