Função modular é a função f: A→ B, em que a lei de formação contém, pelo menos, uma variável dentro do módulo. O módulo ou valor absoluto de um número é representado por |n|, que gera como resultado o valor absoluto, ou seja, um número real positivo.
Existem diferentes tipos de funções modulares, a depender do tipo de equação que se encontra dentro do módulo, podendo ser uma equação do 1º grau, do 2º grau, entre outros tipos de expressões algébricas. Encontramos o valor numérico de uma função quando substituímos a variável pelo valor desejado, então o valor numérico da função quando x = k é igual a f(k). Durante o estudo da função, a representação gráfica também é muito importante para analisarmos o comportamento da variável.
Leia também: Função exponencial - a função em que a variável está no expoente
Tópicos deste artigo
- 1 - Resumo sobre função modular
- 2 - Videoaula sobre função modular
- 3 - O que é uma função modular?
- 4 - Propriedades da função modular
- 5 - Valor numérico de uma função modular
- 6 - Gráfico de uma função modular
- 7 - Exercícios resolvidos sobre função modular
Resumo sobre função modular
- Uma função é modular quando existir uma variável dentro do módulo em sua lei de formação.
- O valor numérico da função é encontrado quando substituímos x pelo valor desejado.
- A função modular pode ter em seu módulo qualquer tipo de equação, como uma equação de 1º ou 2º grau.
Videoaula sobre função modular
O que é uma função modular?
Classificamos uma função como modular quando essa função for f : A → B e, em sua lei de formação, existir uma variável que esteja dentro do módulo.
Exemplos:
- f(x) = |x|
- f(x) = |x² – 3x + 5|
- h(x) = |sen (x)|
- i(x) = |2x + 1| – 4
Para compreender o que é uma função modular, é importante lembrarmos o que é o módulo de um número. O módulo de número n por |n|, por definição, é:
![]()
Vejamos alguns exemplos a seguir:
- |4| → Sabemos que 4 > 0 → |4| = 4
- |-3| → Sabemos que -3 < 0 → |-3| = – (-3) = 3
Note que o módulo de um número é sempre o seu valor absoluto, ou seja, sempre positivo.
|-2,4| = 2,4
|1000| = 1000
Leia também: Como resolver equações com módulo?
Propriedades da função modular
Quando estudamos função modular, é importante compreendermos as principais propriedades do módulo de um número, vejamos as propriedades a seguir:
Para compreender as propriedades, considere n e m como dois números reais.
- 1ª propriedade: o módulo de um número real é igual ao módulo do seu oposto.
|n| = |-n|
- 2ª propriedade: o módulo do produto é igual ao produto dos módulos.
|n · m| = |n| · |m|
- 3ª propriedade: o módulo da soma de dois números é menor ou igual à soma do módulo de cada um deles.
|n + m| ≤ |n| + |m|
- 4ª propriedade: o módulo da diferença é maior ou igual à diferença dos módulos.
|n – m| ≥ |n| – |m|
- 5ª propriedade: o módulo do quadrado de n é igual ao módulo de n ao quadrado.
|n²| = |n|²
Valor numérico de uma função modular
Para encontrar o valor numérico de uma função modular, basta substituir a sua variável pelo valor desejado, vejamos um exemplo a seguir:
Exemplo: f(x) = |-x² + 4x| – 3
a) Encontre f (5).
f(5) = |-5² + 4 · 5| – 3
f(5) = |-25 + 20| – 3
f(5) = |-5| – 3
f(5) = 5 – 3
f(5) = 2
b) Encontre f(-3).
f(-3) = | – (-3)² + 4 · (-3)| – 3
f(-3) = |-9 – 12| – 3
f(-3) = |-21| – 3
f(-3) = 21 – 3
f(-3) = 18
Leia também: Função polinomial — a função que tem um polinômio em sua lei de formação
Gráfico de uma função modular
A representação gráfica é bastante comum no estudo de funções. O gráfico da função modular possui um comportamento que depende do polinômio que está na lei de formação dessa função. Vejamos, a seguir, alguns exemplos de gráfico de função modular.
- Exemplo 1: f(x) = |x + 1|
Analisando o gráfico, podemos dividir ele em dois casos:
f(x) = x + 1 → se x + 1 ≥ 0
f(x) = -x – 1 → se x + 1 < 0
Primeiro encontraremos o zero da função.
|x + 1| = 0
x + 1 = 0
x = -1
Sabemos que o ponto A (-1, 0) pertence ao gráfico dessa função. Agora escolheremos um valor menor e um valor maior para x.
Escolhendo x = -2:
f(-2) = |-2 + 1| = |-1| = 1
B (-2, 1)
Agora, faremos x = 0:
f(0) = |0 + 1| = |1| = 1
C(0, 1)
Então marcaremos os três pontos no gráfico e faremos a representação dessa função:
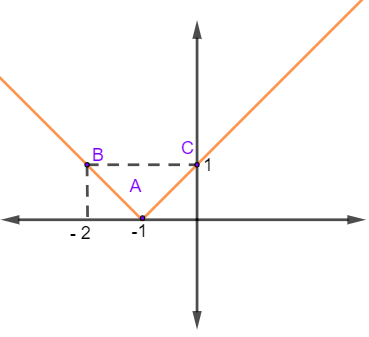
- Exemplo 2: f(x) = |x² – 4|
Primeiro encontraremos o zero da função:
x² – 4 = 0
x² = 4
x = ±√4
x = ±2
Então, temos que x1 = 2 e x2 = -2
Encontraremos o vértice da função. Primeiro somamos os zeros e dividimos por 2 para encontrar o xv.
xv = (-2 + 2) : 2 = 0 : 2 = 0
Substituindo o valor de x = 0, encontraremos yv:
yv = |0² – 4| = |-4| = 4
Assim, encontramos os pontos A(-2, 0), B(2, 0) e C(0, 4), e faremos a representação gráfica da função:
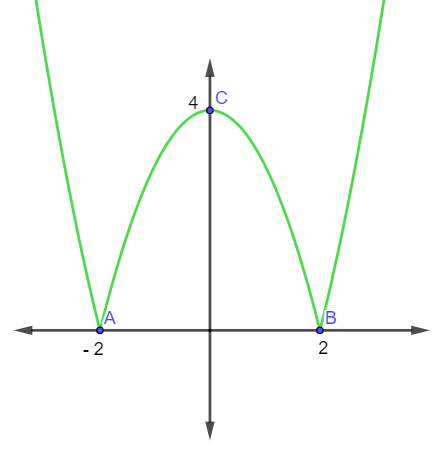
Exercícios resolvidos sobre função modular
Questão 1
Seja f(x) = |2x – 6|, existem dois valores a e b, tal que m ≠ n, mas f(m) = f(n) = 2. Então, o valor de m · n é:
A) 8
B) 6
C) 4
D) 2
E) 1
Resolução:
Alternativa A
Como essa é uma função modular, vamos separar em dois casos:
Suponha que 2m – 6 ≥ 0, então, temos que:
f(m) = 2m – 6
2m – 6 = 2
2m = 2 + 6
2m = 8
m = 8 : 2
m = 4
Agora, suponha que 2n – 6 < 0:
f(n) = – (2n – 6)
– (2n – 6) = 2 (-1)
2n – 6 = -2
2n = -2 + 6
2n = 4
n = 4 : 2
n = 2
Dessa forma, o produto n · m = 4 · 2 = 8
Questão 2
(BIO-Rio) Se f(x) = |x – 3| – |4 – x|, x real, então f(-3) é igual a:
A) -2
B) -1
C) 5
D) 7
Resolução:
Alternativa B
Calculando f(-3), temos que:
f(-3) = |-3 – 3| – |4 – (-3)|
f(-3) = |-6| – |4 + 3|
f(-3) = 6 – (7)
f (-3) = 6 – 7
f(-3) = -1
Por Raul Rodrigues de Oliveira
Professor de Matemática


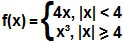 . Pede-se:
. Pede-se: