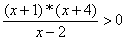A inequação produto e a inequação quociente são casos particulares de inequação. Conhecemos como inequação produto o produto entre duas expressões algébricas em um dos membros da inequação. Já a inequação quociente se dá quando há uma divisão entre duas expressões algébricas em um dos membros da inequação.
Para encontrar o conjunto de soluções da inequação produto, é feito o estudo de sinal de cada um dos seus fatores e depois é analisado qual será o sinal do produto. De modo análogo, para encontrar o conjunto de soluções da inequação quociente, é feito o estudo do sinal do numerador e do denominador separadamente e depois é analisado qual será o sinal do quociente.
Leia também: Inequações logarítmicas — casos em que a incógnita pertence ao logaritmando ou à base
Tópicos deste artigo
- 1 - Resumo sobre inequação produto e inequação quociente
- 2 - Inequação produto
- 3 - Inequação quociente
- 4 - Exercícios resolvidos sobre inequação produto e inequação quociente
Resumo sobre inequação produto e inequação quociente
- Inequação produto se dá quando há um produto entre expressões algébricas na inequação.
- Inequação quociente se dá quando há uma divisão entre expressões algébricas na inequação.
- Para encontrar o conjunto de soluções de uma inequação produto, são necessários o estudo de sinal das funções representadas por cada uma das expressões algébricas e a análise do produto desses sinais.
- Para encontrar o conjunto de soluções de uma inequação quociente, é necessário fazer o estudo de sinal do numerador e do denominador.
Inequação produto
Conhecemos como inequação produto aquela que possui o produto entre duas expressões algébricas em um dos membros da inequação.
Exemplos:
- \( (x-2)(x+3)\geq0\)
- \( (3x-4)(x-8)<0\)
- \( (2x+3)(4x-7)\le0\)
-
Como resolver uma inequação produto
O conjunto de soluções de uma inequação são os valores que x pode assumir sendo que ainda assim ela continue verdadeira. Para encontrar o conjunto de soluções de uma inequação produto, são necessários:
- o estudo de sinal das funções representadas por cada uma das expressões algébricas;
- a análise do produto desses sinais.
Exemplo:
Encontre o conjunto de soluções da inequação a seguir:
(x – 3) (2x – 10) < 0
Resolução:
Primeiramente, faremos o estudo de sinal de cada uma das expressões algébricas.
x – 3 = 0
x = 3
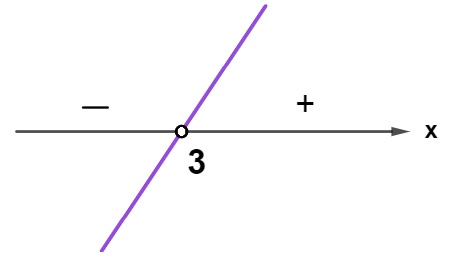
Agora, faremos o estudo de sinal do segundo fator:
\(2x-10=0\)
\(2x=10\)
\(x=\frac{10}{2}\)
\(x=5\)
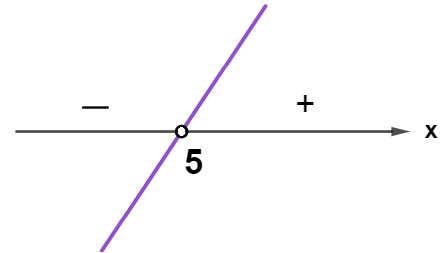
Para que a multiplicação de dois fatores seja menor que zero, os dois fatores precisam ter sinais opostos, ou seja, um positivo e o outro negativo. Analisemos o sinal do produto:
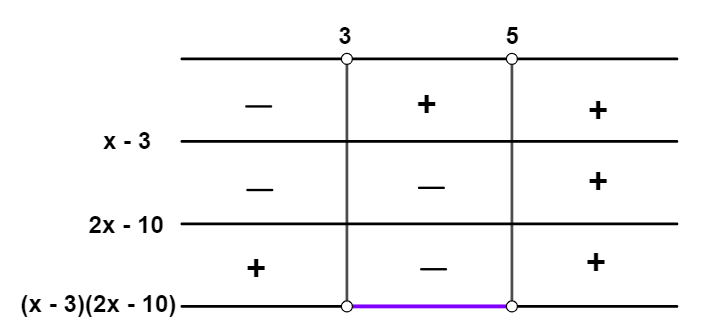
Assim, a inequação (x – 3) (2x – 10) < 0 possui como solução os números maiores que 3 e menores que 5, ou seja 3 < x < 5.
Saiba mais: Como ocorre a localização de qualquer ponto no plano cartesiano?
Inequação quociente
Uma inequação é conhecida como inequação quociente quando ela possui em um dos membros da inequação o quociente entre duas expressões algébricas.
Exemplos:
- \( \frac{x+2}{x-3}\geq0\)
- \( \frac{2x-1}{x+6}<0\)
- \( \frac{5-x}{2+3x}>0\)
-
Como resolver uma inequação quociente
Para encontrar o conjunto de soluções de uma inequação quociente, são necessários:
- o estudo de sinal das funções representadas no numerador do quociente;
- o estudo de sinal das funções representadas no denominador do quociente.
Exemplo:
Encontre o conjunto de soluções da inequação a seguir:
\(\frac{x-6}{2x-2}>0\)
Resolução:
De início, faremos o estudo de sinal do numerador:
\(x-6=0\)
\(x=6\)
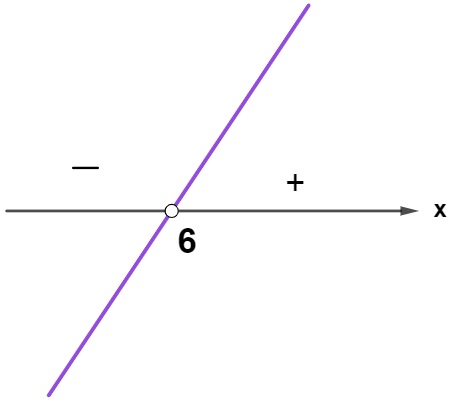
Agora, analisando o denominador:
\(2x-2=0\)
\(2x=2\)
\(x=\frac{2}{2}\)
\(x=1\)
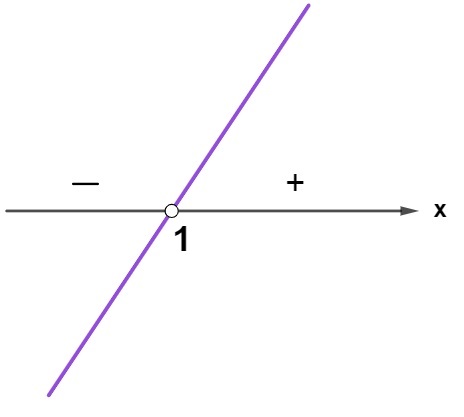
Para que a divisão tenha resultado positivo, ou o numerador e o denominador devem ser positivos, ou ambos devem ser negativos:
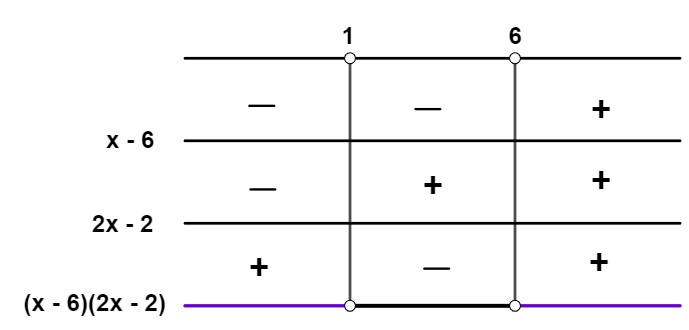
Portanto, a solução dessa inequação é a união dos intervalos x < 1 ou x > 6.
Exercícios resolvidos sobre inequação produto e inequação quociente
Questão 1
(Vunesp) Os números reais que satisfazem a inequação (x + 1) (x – 2) (x – 3) > 0 são descritos por:
A) x > 3
B) x < – 1
C) x > 2
D) –1 < x < 2 e x > 3
E) –1 < x < 2 ou x > 3
Resolução:
Alternativa E
Primeiramente, faremos o estudo de sinal para cada um dos fatores, encontrando o 0 de cada uma delas:
x + 1 = 0
x = – 1
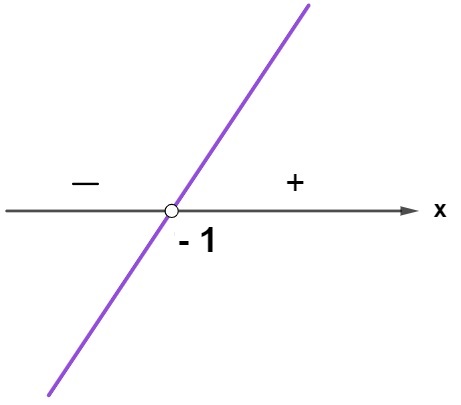
x – 2 = 0
x = 2
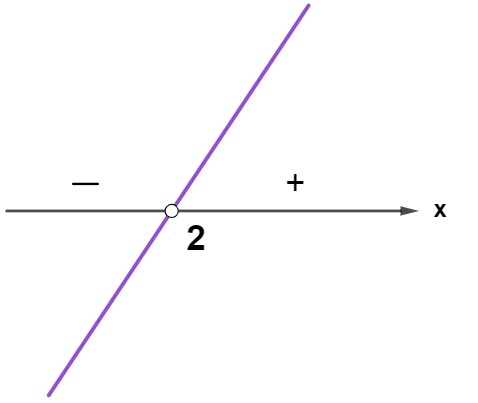
x – 3 = 0
x = 3
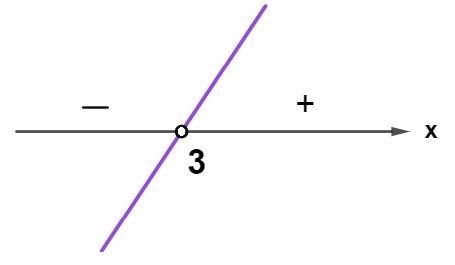
Analisando o sinal do produto, temos que:
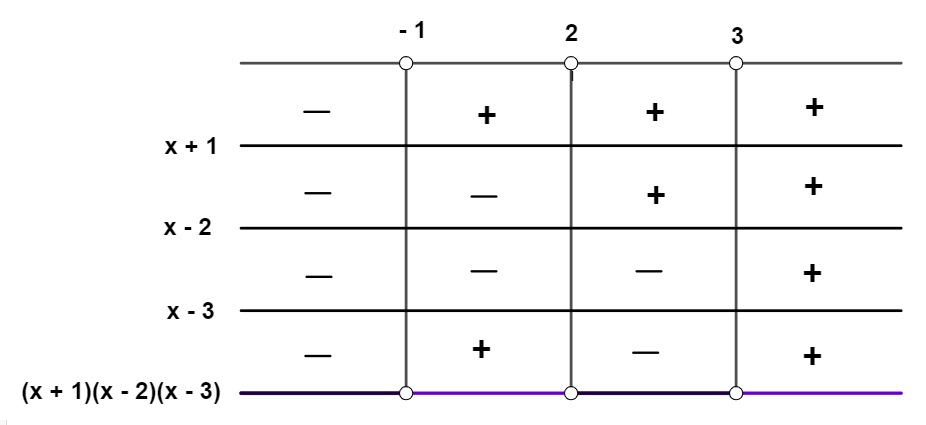
Assim, as soluções desse conjunto são –1 < x < 2 ou x > 3.
Questão 2
Analise a inequação a seguir:
\(\frac{x-3}{5-x}\le0\)
Sobre essa inequação, podemos afirmar que:
I. É uma inequação quociente.
II. x = 2 é uma solução para a inequação.
III. x = 5 é uma solução da inequação.
Marque a alternativa correta:
A) Somente I é falsa.
B) Somente II é falsa.
C) Somente III é falsa.
D) Todas são verdadeiras.
Resolução:
Alternativa C
I. Verdadeira
Note que há uma razão entre duas expressões algébricas, logo essa é uma inequação quociente.
II. Verdadeira
Para verificar se 2 é solução, substituiremos x = 2 na inequação:
\(\frac{2-3}{5-2}\le0\)
\(\frac{-1}{3}\le0\)
\(\frac{-1}{3}\le0\)
Sabemos que \(\frac{-1}{3}\) é menor que 0, logo x = 2 é uma solução.
III. Falsa
Se x = 5, note que o denominador seria 0, sendo que é impossível dividir por 0. Logo, x deve ser diferente de 5.
Por Raul Rodrigues de Oliveira
Professor de Matemática