Função Composta

Uma função é uma regra que relaciona cada elemento de um conjunto, chamado domínio, a um único elemento de outro conjunto, chamado contradomínio. Suponha que existam duas funções, f e g, em que o domínio da função g é igual ao contradomínio da função f. Nesse caso, é possível criar uma função gof, chamada de função composta, a qual relaciona diretamente os elementos do domínio da função f aos elementos do contradomínio da função g.

Definição de função composta

Dadas as funções f: A → B e g: B → C, a função composta de g com f é a função h(x) = g(f(x)), que também pode ser representada como gof(x) – que é lida como “g bola f de x”.

Para utilizar a função h, podemos aplicar a função f no ponto x, descobrir qual é o valor do contradomínio relacionado a ele e aplicar a função g sobre esse valor. Fazendo isso, obteremos um ponto do contradomínio de g cujos pontos de seu domínio também pertençam ao contradomínio da f.

Sendo assim, a função h, seu domínio e contradomínio ficam definidos como:

h: A → C

Isso porque, pelo fato de ser igual à composta de g com f, a função h relaciona cada elemento do domínio da função f com um único elemento do contradomínio da função g.

Diagrama

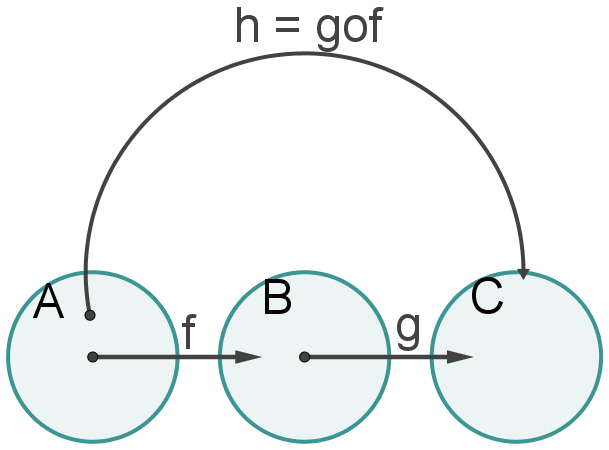
O diagrama a seguir mostra o comportamento das funções f, g e h. Nesse diagrama, observe que a função f, representada pela primeira flecha, relaciona elementos do conjunto A a elementos do conjunto B:

A segunda flecha representa a função g, que relaciona elementos do conjunto B a elementos do conjunto C. Para relacionar elementos do conjunto A a elementos do conjunto B, existem dois caminhos: utilizar as duas funções uma a uma ou construir a função composta gof, que, como mostra o diagrama, relaciona diretamente elementos do conjunto A a elementos do conjunto C.

Funções compostas na prática

Na prática, construir a função composta é um processo simples. Para construir a composta gof, por exemplo, deveremos substituir a variável da função g por toda a função f.

Exemplo: dadas as funções f(x) = 2x³ e g(x) = 2x + 3x², todas com domínio e contradomínio igual ao conjunto dos números reais, teremos:

gof(x) = 2(2x³) + 3(2x³)²

gof(x) = 4x³ + 3·4x⁶

gof(x) = 4x³ + 12x⁶
 

fog(x) = 2(2x + 3x²)³

Por Luiz Paulo Moreira
Graduado em Matemática