Relação entre parábola e coeficientes de uma função do segundo grau

Uma função do segundo grau é uma regra que relaciona cada elemento de um conjunto A a um único elemento de um conjunto B e que pode ser escrita na seguinte forma:

f(x) = ax² + bx + c

Os coeficientes de uma função do segundo grau são os números representados nessa expressão pelas letras a, b e c. Já a letra x é chamada variável.

Toda função do segundo grau pode ser representada graficamente por uma parábola. Algumas das características dessa figura geométrica podem ser relacionadas com os coeficientes da função do segundo grau.

Coeficiente A

O coeficiente a indica a concavidade de uma função do segundo grau.

Se a > 0, então a concavidade da parábola é voltada para cima.

Se a < 0, então a concavidade da parábola é voltada para baixo.

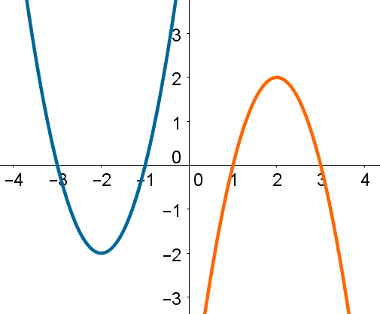
A imagem a seguir mostra uma parábola à esquerda que possui concavidade voltada para cima e outra, à direita, com a concavidade voltada para baixo.

Assim, podemos concluir que o coeficiente a na parábola à esquerda é positivo e, na parábola à direita, é negativo.

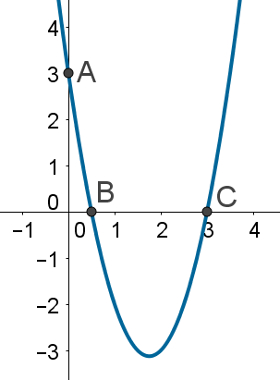
Além disso, o coeficiente a também é responsável pela “abertura” da parábola. Quanto maior o valor do módulo do coeficiente, menor será a abertura. Para compreender melhor esse conceito, observe os pontos A e B na parábola a seguir:

Quanto maior o valor do módulo do coeficiente a, menor será a distância entre os pontos A e B.

Coeficiente C

Em uma função do segundo grau, o coeficiente C sempre representará o ponto de encontro do eixo y com a parábola. Algebricamente, é possível notar isso fazendo x = 0 em uma função do segundo grau:

f(x) = ax² + bx + c

f(0) = a0² + b0 + c

f(0) = c

Logo, o ponto (0, c) sempre faz parte do gráfico de qualquer função do segundo grau e, como x = 0, então, esse ponto está sobre o eixo y.

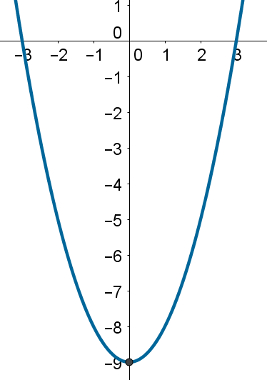
Por exemplo, o gráfico da função f(x) = x² – 9 é:

Note que o ponto de encontro do eixo y com o gráfico da parábola é o ponto (0, – 9). Essa regra é válida para toda função do segundo grau.

Valor de delta (discriminante)

Calcular o discriminante é o primeiro passo a ser dado para encontrar as raízes de uma função do segundo grau. Seu valor é encontrado substituindo os coeficientes da função do segundo grau na fórmula:

∆ = b² – 4·a·c

O valor numérico de ∆ indica a quantidade de raízes reais que uma função do segundo grau possui.

Se ∆ > 0, a função possui duas raízes reais distintas.

Se ∆ = 0, a função possui uma raiz real.

Se ∆ < 0, a função não possui raízes reais.

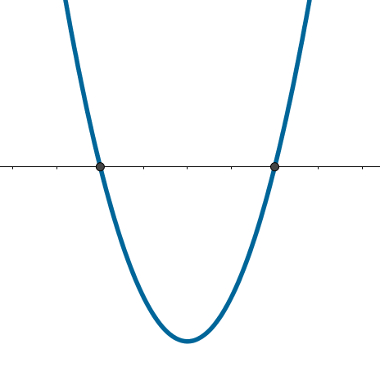
Se esse conhecimento for aliado ao coeficiente a de uma função do segundo grau, poderemos descobrir muito sobre uma função. Na função f(x) = x² – 16, o valor de ∆ nessa função é:

∆ = b² – 4·a·c

∆ = 0² – 4·1·(– 16)

∆ = 4·16

∆ = 64

Além disso, observe que a = 1 > 0. Assim, essa função toca o eixo x duas vezes e tem a concavidade voltada para cima, o que significa que seu vértice é ponto de mínimo e terá um desenho parecido com:

Por Luiz Paulo Moreira
Graduado em Matemática