Uma função é chamada de função polinomial quando a sua lei de formação é um polinômio. As funções polinomiais são classificadas de acordo com o grau de seu polinômio. Por exemplo, se o polinômio que descreve a lei de formação da função tiver grau dois, dizemos que essa é uma função polinomial do segundo grau.
Para calcular o valor numérico de uma função polinomial, basta substituir a variável pelo valor desejado, transformando o polinômio em uma expressão numérica. No estudo de funções polinomiais, é bastante recorrente a representação gráfica. A função polinomial do 1º grau tem gráfico sempre igual a uma reta. Já a função do 2º grau possui gráfico igual a uma parábola.
Leia também: Quais as diferenças entre equação e função?
Tópicos deste artigo
- 1 - O que é uma função polinomial?
- 2 - Como determinar o tipo de função polinomial?
- 3 - Grau da função polinomial
- 4 - Valor numérico da função
- 5 - Gráficos de função polinomial
- 6 - Igualdade de polinômios
- 7 - Operações com polinômios
- 8 - Exercícios resolvidos
O que é uma função polinomial?

Uma função f : R → R é conhecida como função polinomial quando a sua lei de formação é um polinômio:
f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a2x2 + a1x + a0
Em que:
x → é a variável.
n → é um número natural.
an, an-1, an-2, … a2, a1 e a0 → são coeficientes.
Os coeficientes são números reais que acompanham a variável do polinômio.
Exemplos:
-
f(x) = x5 + 3x4 – 3x3 + x² – x + 1
-
f(x) = -2x³ + x – 7
-
f(x) = x9
Como determinar o tipo de função polinomial?
Existem vários tipos de função polinomial. Ela é classificada de acordo com o grau do polinômio. Quando o grau for 1, então, a função é conhecida como função polinomial de grau 1 ou função polinomial do 1º grau ou, também, função afim. Veja, a seguir, exemplos de função de grau 1 até o grau 6.
Veja também: O que é uma função injetora?
Grau da função polinomial
O que define o grau da função polinomial é o grau do polinômio, então, podemos ter uma função polinomial de qualquer grau.
-
Função polinomial de grau 1
Para que uma função polinomial seja de grau 1 ou polinomial do 1º grau, a lei de formação da função deve ser f(x) = ax + b, com a e b sendo números reais e a ≠ 0. A função polinomial de grau 1 é conhecida também como função afim.
Exemplos:
-
f(x) = 2x – 3
-
f(x) = -x + 4
-
f(x) = -3x
-
Função polinomial de grau 2
Para que uma função polinomial seja de grau 2 ou polinomial do 2º grau, a lei de formação da função deve ser f(x) = ax² + bx + c, com a, b e c sendo números reais e a ≠ 0. Uma função polinomial do 2º grau pode ser conhecida também como função quadrática.
Exemplos:
-
f(x) = 2x² – 3x + 1
-
f(x) = – x² + 2x
-
f(x) = 3x² + 4
-
f(x) = x²
-
Função polinomial de grau 3
Para que uma função polinomial seja de grau 3 ou polinomial do 3º grau, a lei de formação da função deve ser f(x) = ax³ + bx² + cx + d, com a e b sendo números reais e a ≠ 0. A função de grau 3 pode se chamar também de função cúbica.
Exemplos:
-
f(x) = 2x³ – 3x² + 2x + 1
-
f(x) = -5x³ + 4x² + 2x
-
f(x) = 3x³ + 8x – 4
-
f(x) = -7x³
-
Função polinomial de grau 4
Tanto para a função polinomial de grau 4 quanto para as demais, o raciocínio é o mesmo.
Exemplos:
-
f(x) = 2x4 + x³ – 5x² + 2x + 1
-
f(x) = x4 + 2x³ – x
-
f(x) = x4
-
Função polinomial de grau 5
Exemplos:
-
f(x) = x5 – 2x4 + x3 – 3x² + x + 9
-
f(x) = 3x5 + x3 – 4
-
f(x) = -x5
-
Função polinomial de grau 6
Exemplos:
-
f(x) = 2x6 – 7x5 + x4 – 5x3 + x² + 2x – 1
-
f(x) = -x6 + 3x5 + 2x³ + 4x + 8
-
f(x) = 3x6 + 2x² + 5x
-
f(x) = x6
Valor numérico da função
Conhecendo a lei de formação da função f(x), para calcular o valor numérico da função para um valor n, basta calcular o valor de f(n). Para tanto, substituímos a variável na lei de formação.
Exemplo:
Dada a função f(x) = x³ + 3x² – 5x + 4, encontramos o valor numérico da função para x = 2.
Para encontrar o valor de f(x) quando x = 2, faremos f(2).
f(2) = 2³ + 3 · 2² – 5 · 2 + 4
f(2) = 8 + 3 · 4 – 5 · 2 + 4
f(2) = 8 + 12 – 10 + 4
f(2) = 20 – 10 + 4
f(2) = 10 + 4
f(2) = 14
Podemos dizer que a imagem da função ou o valor numérico da função, quando x = 2, é igual a 14.
Veja também: Função inversa – consiste no inverso da função f(x)
Gráficos de função polinomial
Para representar no plano cartesiano a função, representamos, no eixo x, os valores de x, e a imagem de f(x), por pontos no plano. Os pontos no plano cartesiano são do tipo (n, f(n)).
Exemplo 1:
-
f(x) = 2x – 1
O gráfico de uma função de 1º grau é sempre uma reta.
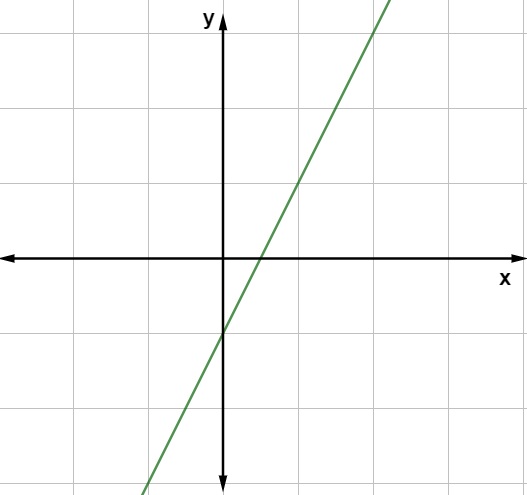
Exemplo 2:
-
f(x) = x² – 2x – 1
O gráfico da função de 2º grau é sempre uma parábola.
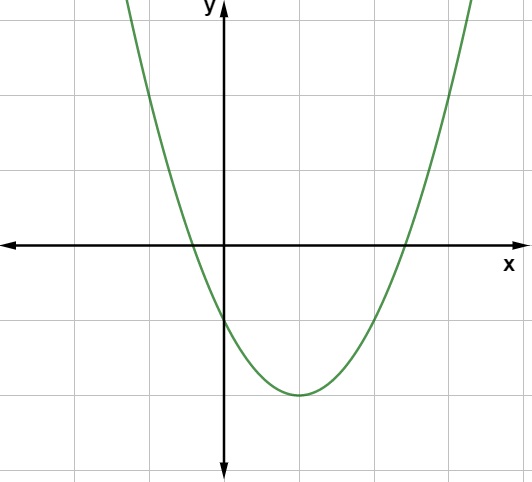
Exemplo 3:
-
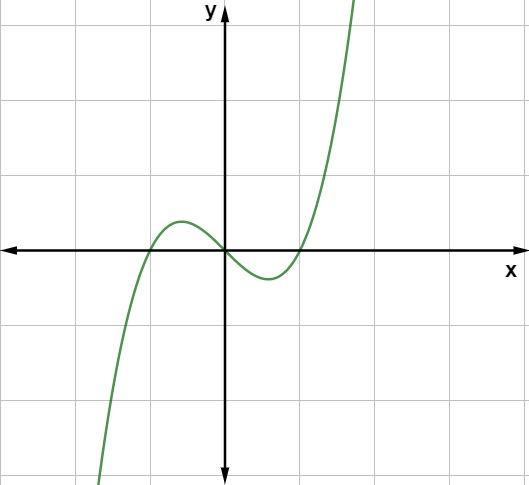
f(x) = x³ – x
O gráfico da função de 3º grau é conhecido como cúbica.
Igualdade de polinômios
Para que dois polinômios sejam iguais, é necessário que, ao fazermos a comparação entre os seus termos, os coeficientes sejam os mesmos.
Exemplo:
Dados os polinômios p(x) e g(x) a seguir, e sabendo que p(x) = g(x), encontre o valor de a, b, c, e d.
p(x) = 2x³ + 5x² + 3x – 4
g(x) = ax³ + (a + b) x² + (c – 2) x + d
Como os polinômios são iguais temos, que:
ax³ = 2x³
(a + b)x² = 5x²
(c – 2)x = 3x
d = -4
Note que já temos o valor de d, pois d = -4. Agora, calculando cada um dos coeficientes, temos que:
ax³ = 2x³
a = 2
Conhecendo o valor de a, vamos encontrar o valor de b:
(a + b)x² = 5x²
a + b = 5
a = 2
2 + b = 5
b = 5 – 2
b = 3
Encontrando o valor de c:
(c – 2)x = 3x
c – 2 = 3
c = 3 + 2
c = 5
Veja também: Equação polinomial – equação caracterizada por ter um polinômio igual a 0
Operações com polinômios
Dados dois polinômios, é possível realizar as operações de adição, subtração e multiplicação entre esses termos algébricos.
-
Adição
A adição de dois polinômios é calculada pela soma dos termos semelhantes. Para que dois termos sejam semelhantes, a parte literal (letra com o expoente) deve ser a mesma.
Exemplo:
Seja p(x) = 3x² + 4x + 5 e q(x) = 4x² – 3x + 2, calcule o valor de p(x) + q(x).
3x² + 4x + 5 + 4x² – 3x + 2
Destacando os termos semelhantes:
3x² + 4x + 5 + 4x² – 3x + 2
Agora vamos realizar a soma dos coeficientes dos termos semelhantes:
(3 + 4)x² + (4 – 3)x + 7
7x² + x + 7
-
Subtração de polinômios
A subtração é bastante semelhante à adição, porém, antes de realizar a operação, escrevemos o polinômio oposto.
Exemplo:
Dados: p(x) = 2x² + 4x + 3 e q(x) = 5x² – 2x + 1, calcule p(x) – q(x).
O polinômio oposto de q(x) é o -q(x), que nada mais é que o polinômio q(x) com o oposto de cada um dos termos.
q(x) = 5x² – 2x + 1
-q(x) = -5x² + 2x – 1
Então, calcularemos:
2x² + 4x + 3 – 5x² + 2x – 1
Simplificando os termos semelhantes, temos:
(2 – 5)x² + (4 + 2)x + (3 – 1)
-3x² + 6x + 2
-
Multiplicação de polinômios
Multiplicar polinômio exige a aplicação da propriedade distributiva, ou seja, multiplicamos cada um dos termos do primeiro polinômio por cada um dos termos do segundo termo.
Exemplo:
(x + 1) · (x² + 2x – 2)
Aplicando a propriedade distributiva, temos que:
x · x² + x · 2x + x · (-2) + 1 · x² + 1 · 2x + 1 · (-2)
x3 + 2x² + -2x – 2 + x² + 2x + -2
x³ + 3x² – 4
-
Divisão de polinômios
Para calcular a divisão entre dois polinômios, recorremos ao mesmo método que utilizamos para calcular a divisão de dois números, o método de chaves.
Exemplo:
Calcule p(x) : q(x), sabendo que p(x) = 15x² + 11x + 2 e q(x) = 3x + 1.
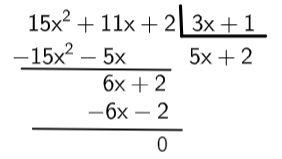
Leia também: Dispositivo prático de Briot-Ruffini – outro método para calcular a divisão de polinômios
Exercícios resolvidos
Questão 1 - O custo de produção diária de uma indústria de peças automotivas para produzir uma determinada quantidade de peças é dado pela lei de formação f(x) = 25x + 100, em que x é o número de peças produzidas naquele dia. Sabendo que, em um determinado dia, foram produzidas 80 peças, o custo de produção dessas peças foi de:
A) R$ 300
B) R$ 2100
C) R$ 2000
D) R$ 1800
E) R$ 1250
Resolução
Alternativa B
f(80) = 25 · 80 + 100
f(80) = 2000 + 100
f(80) = 2100
Questão 2 - O grau da função h(x) = f(x) · g(x), sabendo que f (x) = 2x² + 5x e g(x) = 4x – 5, é:
A) 1
B) 2
C) 3
D) 4
E) 5
Resolução
Alternativa C
Primeiro encontraremos o polinômio que é resultado da multiplicação entre f(x) e g(x):
f(x) · g(x) = (2x² + 5x) · (4x – 5)
f(x) · g(x) = 8x³ – 10x² + 20x – 25x
Note que esse é um polinômio é de grau 3, logo, o grau da função h(x) é 3.
Por Raul Rodrigues de Oliveira
Professor de Matemática


