Trabalhar com funções compostas não apresenta grandes segredos, mas requer muita atenção e cuidado. Quando lidamos com uma composição de três ou mais funções, sejam elas do 1º grau ou do 2º grau, maior deve ser a preocupação. Antes de analisar alguns exemplos, vamos compreender a ideia central da composição de funções.
Imagine que você pretende fazer uma viagem de avião saindo do Rio Grande do Sul com destino ao Amazonas. Uma empresa aérea oferece uma passagem de voo direto e outra opção mais econômica, com três pontes aéreas, conforme o esquema a seguir:
Rio Grande do Sul → São Paulo → Goiás → Amazonas
Qualquer uma das opções de viagem levará ao destino pretendido, e assim também ocorre com a função composta. Veja a imagem a seguir:
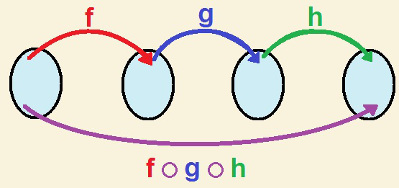
Exemplo de como funciona uma composição de três funções
Que tal utilizarmos esse esquema para aplicar um exemplo? Considere então as seguintes funções: f(x) = x + 1, g(x) = 2x – 3 e h(x) = x². A composição f o g o h (lê-se: f composta com g composta com h) pode ser mais facilmente interpretada ao ser expressa como f(g(h(x))). Para resolver essa composição de funções, devemos começar pela função composta mais interna ou pela última composição, portanto, g(h(x)). Na função g(x) = 2x – 3, onde houver x, substituiremos por h(x):
g(x) = 2x – 3
g(h(x)) = 2.h(x) – 3
g(h(x)) = 2.(x²) – 3
g(h(x)) = 2.x² – 3
Agora faremos a última composição f(g(h(x))). Na função f(x) = x + 1, onde houver x, substituiremos por g(h(x)) = 2.x² – 3:
f(x) = x + 1
f(g(h(x))) = (2.x² – 3) + 1
f(g(h(x))) = 2.x² – 3 + 1
f(g(h(x))) = 2.x² – 2
Vejamos um exemplo para comprovar que, assim como aconteceu no caso do voo citado no início deste artigo, se escolhermos um valor para aplicar em f(g(h(x))), obteremos o mesmo resultado que ao aplicar separadamente nas composições. Se x = 1, temos que h(1) é igual a:
h(x) = x²
h(1) = 1²
h(1) = 1
Sabendo que h(1) = 1, vamos agora encontrar o valor de g(h(1)):
g(x) = 2x – 3
g(h(1)) = 2.h(1) – 3
g(h(1)) = 2.1 – 3
g(h(1)) = – 1
Por fim, vamos calcular o valor de f(g(h(1))), sabendo que g(h(1)) = – 1:
f(x) = x + 1
f(g(h(1))) = g(h(1)) + 1
f(g(h(1))) = – 1 + 1
f(g(h(1))) = 0
Encontramos que f(g(h(1))) = 0. Dessa forma, vamos ver se obtemos o mesmo resultado ao substituir x = 1 na fórmula da composição de funções que encontramos anteriormente: f(g(h(x))) = 2.x² – 2:
f(g(h(x))) = 2.x² – 2
f(g(h(1))) = 2.(1)² – 2
f(g(h(1))) = 2 – 2
f(g(h(1))) = 0
Portanto, realmente obtivemos o mesmo resultado como queríamos demonstrar. Vejamos ainda outro exemplo de composição de três ou mais funções:
Sejam as funções: f(x) = x² – 2x, g(x) = – 2 + 3x, h(x) = 5x³ e i(x) = – x, determine a lei da função composta f(g(h(i(x)))).
Começaremos a resolver essa composição pela função composta mais interna, h(i(x)):
i(x) = – x e h(x) = 5x³
h(x) = 5x³
h(i(x)) = 5.[i(x)]³
h(i(x)) = 5.[– x]³
h(i(x)) = – 5x³
Vamos agora resolver a composição g(h(i(x))):
h(i(x)) = – 5x³ e g(x) = – 2 + 3x
g(x) = – 2 + 3x
g(h(i(x))) = – 2 + 3.[h(i(x))]
g(h(i(x))) = – 2 + 3.[– 5x³]
g(h(i(x))) = – 2 – 15x³
Podemos agora determinar a lei da função composta f(g(h(i(x)))):
g(h(i(x))) = – 2 – 15x³ e f(x) = x² – 2x
f(x) = x² – 2x
f(g(h(i(x)))) = [g(h(i(x)))]² – 2[g(h(i(x)))]
f(g(h(i(x)))) = [– 2 – 15x³]² – 2[– 2 – 15x³]
f(g(h(i(x)))) = 4 – 60x³ + 225x6 + 4 + 30x³
f(g(h(i(x)))) = 225x6 – 30x³ + 8
Portanto, a lei da função composta f(g(h(i(x)))) é f(g(h(i(x)))) = 225x6 – 30x³ + 8
Por Amanda Gonçalves
Graduada em Matemática
