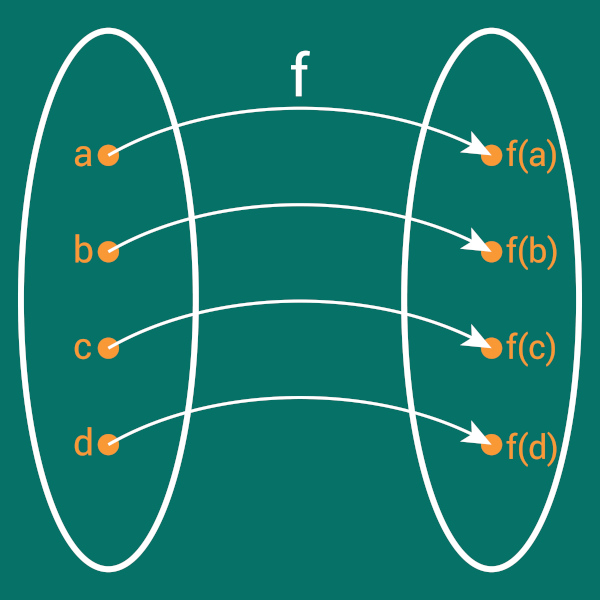
A função bijetora, chamada também de bijetiva, é a função que é sobrejetora e injetora ao mesmo tempo. Uma função é injetora se, para quaisquer dois elementos distintos do domínio, suas imagens também sejam distintas. Uma função é sobrejetora se o conjunto imagem for igual ao contradomínio, ou seja, todos os elementos do contradomínio são imagem de, pelo menos, um elemento no domínio, então, para que uma função seja bijetora, é necessário que ela satisfaça essas duas condições. Saber se uma função é bijetora ou não é importante porque uma função só admite inversa se ela for bijetora.
Saiba mais: Diferenças entre função e equação
Tópicos deste artigo
- 1 - O que é uma função bijetora?
- 2 - Exemplo de função bijetora
- 3 - Gráfico da função bijetora
- 4 - Gráfico de uma função não bijetora
- 5 - Função inversa
- 6 - Exercícios resolvidos sobre função bijetora
O que é uma função bijetora?
Função é uma relação entre dois conjuntos A, conhecido como domínio, e B, conhecido como contradomínio. Sob uma regra que associa os elementos do conjunto A aos elementos do conjunto B na função, cada elemento do domínio possuirá um único correspondente no contradomínio.
De acordo com as características da função, existem algumas classificações possíveis para ela, e uma delas diz respeito à função ser bijetora ou bijetiva, ou seja, quando a função é injetora e sobrejetora simultaneamente. Então, para saber se uma função é bijetora, verificamos a injetividade e a sobrejetividade.
-
Função injetora: ocorre se, dados quaisquer dois elementos distintos do domínio, as imagens desses elementos também serão distintas, ou seja, f: A → B é injetora se f(a1) ≠ f(a2).
-
Função sobrejetora: ocorre quando todo elemento do contradomínio possuir um correspondente no domínio.
Se a função satisfaz as definições de uma função injetora e de uma função sobrejetora, então ela é classificada como bijetora.
Exemplo de função bijetora
Conhecendo a função \(f: R→R\), com lei de formação \(f(x)=2x\), teremos uma função bijetora.
Nessa função, dados \(x_1\) e \(x_2\), tal que \(x_1≠x_2\), temos que \(f(x_1 )≠f(x_2 )\), pois \(2x_1≠2x_2\). Então f é uma função injetora.
Além disso, sabemos que, dado \(f(x)\) = y como um número real, no contradomínio, para todo y, existirá um valor real x, tal que 2x = y. Para encontrá-lo, basta dividir y por 2, pois, nesse caso, sabemos que y é o dobro de x. Assim, podemos concluir que essa função é sobrejetora.
Como a função é injetora e sobrejetora simultaneamente, então ela é bijetora.
Gráfico da função bijetora
Para verificar se o gráfico de uma função é bijetor para determinado intervalo, é necessário analisar se a função é injetora, e, para isso, analisamos se, ao traçar retas paralelas ao eixo x, essa reta intercepta o gráfico da função em um único ponto. Além disso, para verificar se a função é sobrejetora, analisamos se não existem valores do eixo y que não sejam imagem de nenhum valor do eixo x.
Exemplo:
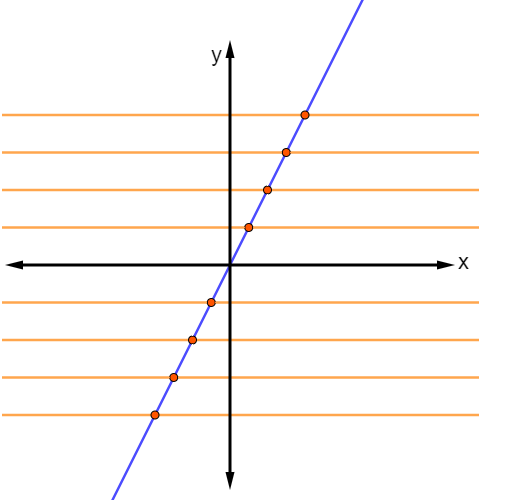
Note que, nesse intervalo, as retas paralelas ao eixo x cortam o gráfico da função em um único ponto, o que faz com que a função seja injetora e que todo valor de y para esse intervalo seja correspondente de um valor de x, o que faz com que ela seja também sobrejetora. Desse modo, para esse intervalo, a função é bijetora.
Vale ressaltar que não sabemos das informações do gráfico da função para além do intervalo representado, e, portanto, sem conhecer a lei de formação, não podemos inferir que a função é totalmente bijetora.
Gráfico de uma função não bijetora
Veja agora um gráfico de uma função que não é bijetora.
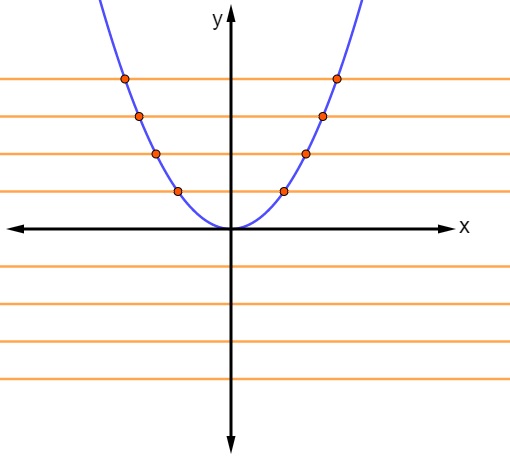
Note que, para uma mesma reta paralela ao eixo x, há mais de um ponto de encontro com o gráfico da função, sendo assim, elementos distintos do domínio x possuem a mesma imagem y, o que faz com que essa função não seja injetora, o que já é suficiente para que ela não seja bijetora. Note também que, na parte debaixo do eixo y, não há gráfico dessa função, então, para esse intervalo, existem valores de y que não são imagens de nenhum valor de x, o que faz com que ela não seja sobrejetora.
Saiba mais: Como construir o gráfico de uma função?
Função inversa
Uma função qualquer só admite inversa se for bijetora. Dada a função \(f: A →B\), sabemos que a função inversa é a \(f^(-1):B→A\).
Para entender por que uma função só admite inversa, vamos relembrar a definição de função. A função é uma relação entre dois conjuntos — domínio e contradomínio —, em que, para todo elemento do domínio, existe um único correspondente no contradomínio.
Se a função não for sobrejetora, ou seja, nem todos os elementos do contradomínio são correspondentes de um elemento no domínio, na função inversa existirá elementos do conjunto B que não possuem imagem no conjunto A, o que contraria a definição de função, logo, para que exista uma função inversa, uma função tem que ser sobrejetora.
Se a função não for injetora, existirá elementos distintos de A que possuem mesma imagem no conjunto B, fazendo com que, ao encontrar a função inversa, um elemento do domínio tenha dois ou mais correspondentes no contradomínio, o que contraria também a definição de função. Então uma função só admite inversa se for injetora.
Exercícios resolvidos sobre função bijetora
Questão 1
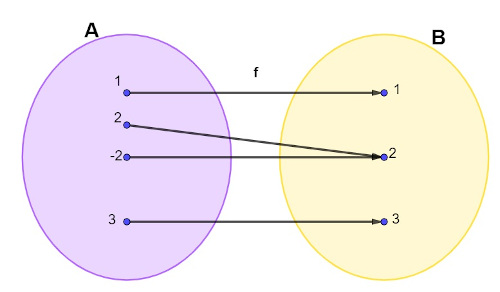
No diagrama a seguir, está representada uma relação entre dois conjuntos A e B:
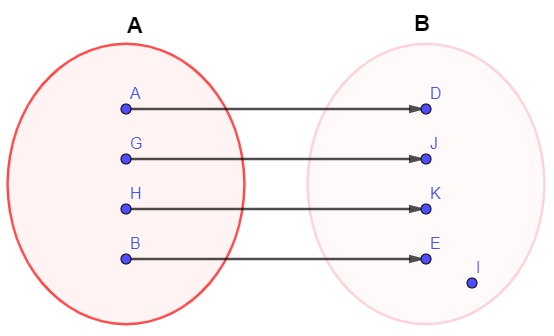
Analisando esse diagrama, podemos afirmar que essa relação:
A) não representa uma função.
B) representa uma função bijetora.
C) representa uma função que não é bijetora, pois ela é injetora, mas não é sobrejetora.
D) representa uma função que não é bijetora, pois ela é sobrejetora, mas não é injetora
Resolução:
Alternativa C
Podemos observar que, para todo elemento do conjunto A, existe um elemento correspondente no conjunto B. Além disso, que essa função é injetora, pois elementos distintos possuem imagens distintas, entretanto, não é sobrejetora, pois existe um elemento no conjunto B que não é correspondente de nenhum elemento no conjunto A, portanto, a função não é bijetora. Desse modo, essa relação entre os dois conjuntos representa uma função que não é bijetora, pois é injetora, mas não é sobrejetora.
Questão 2
Sobre funções injetoras, sobrejetoras e bijetoras, julgue os itens abaixo em verdadeiro ou falso.
I. Toda função injetora é bijetora.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora.
III. Toda função bijetora admite inversa.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora.
A) V - V - V - V
B) F - F - V - V
C) V - V - F - F
D) F - F - F - F
Resolução:
Alternativa B
I. Toda função injetora é bijetora. (falsa)
Para ser bijetora, a função tem que ser injetora e sobrejetora, então existe função que é injetora e que não é bijetora.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora. (falsa)
Essa característica é de uma função injetora.
III. Toda função bijetora admite inversa. (verdadeira)
Toda função bijetora, de fato, admite função inversa.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora. (verdadeira)
Quando a imagem é igual ao contradomínio, de fato, temos uma função sobrejetora.
Por Raul Rodrigues de Oliveira
Professor de Matemática