Função exponencial

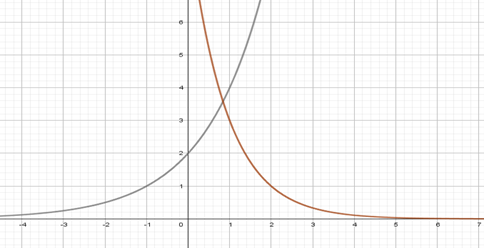
A função exponencial ocorre quando, em sua lei de formação, a variável está no expoente, com domínio e contradomínio nos números reais. O domínio da função exponencial são os números reais, e o contradomínio são os números reais positivos diferentes de zero. A sua lei de formação pode ser descrita por f(x) =a^x, em que a é um número real positivo diferente de 1.

O gráfico de uma função exponencial sempre estará no primeiro e segundo quadrantes do plano cartesiano, podendo ser crescente, quando a for um número maior do que 1, ou decrescente, quando a for um número positivo menor do que 1. A função inversa da função exponencial é a função logarítmica, o que torna os gráficos dessas funções sempre simétricos.

Leia também: O que é função?

Tópicos deste artigo

• 1 - O que é função exponencial?
• 2 - Tipos de função exponencial
• 3 - Gráfico da função exponencial
• 4 - Propriedades da função exponencial
  • → 1ª propriedade
  • → 2ª propriedade
  • → 3ª propriedade
  • → 4ª propriedade
• 5 - Função exponencial e função logarítmica
• 6 - Exercícios resolvidos

O que é função exponencial?

Como o nome sugere, o termo exponencial está ligado a expoente. Então, a definição de função exponencial é uma função cujo domínio é o conjunto dos números reais, e o contradomínio é o conjunto dos números reais positivos não nulos, descrito por : ℝ → ℝ*₊. A sua lei de formação é descrita pela equação f(x) = a^x, em que a é um número real qualquer, positivo, não nulo e que recebe o nome de base.

Exemplos:

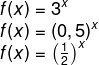
Na lei de formação, f(x) pode ser descrito também como y e, assim como nas demais funções, ele é conhecido como variável dependente, porque seu valor depende de x, que é conhecido como variável independente.

Tipos de função exponencial

As funções exponencias podem ser classificadas em dois casos distintos. Levando em consideração o comportamento da função, ela pode ser crescente ou decrescente.

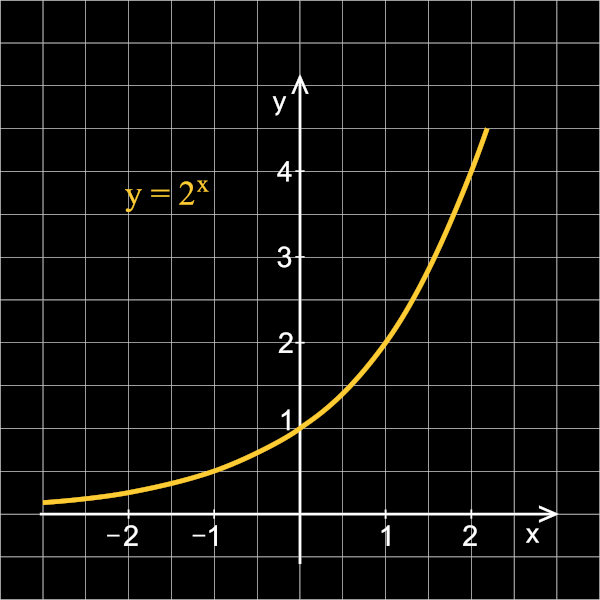
Uma função exponencial é dita crescente se, à medida que o valor de x aumenta, o valor de f(x) também aumenta. Isso ocorre quando a base é maior que 1, ou seja: a > 1.

Exemplo:

Uma função exponencial é considerada decrescente se, à medida que o valor de x aumenta, o valor de f(x) diminui. Isso ocorre quando a base é um número entre 0 e 1, ou seja, 0 < a < 1.

Exemplo:

Leia também: Diferenças entre função e equação

Gráfico da função exponencial

Para desenharmos a representação gráfica de uma função exponencial, é necessário encontrar a imagem para alguns valores do domínio. O gráfico de uma função exponencial tem como característica um crescimento bem maior que o das funções lineares, se for crescente, ou um decrescimento maior, quando decrescente.

Exemplos:

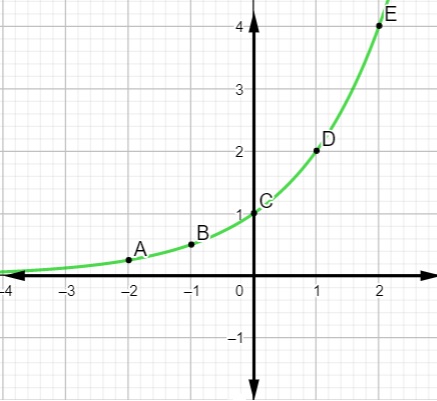
a) Construa o gráfico da função: f(x) = 2^x.

Como a >1, então essa função é crescente. Para a construção do gráfico, vamos atribuir alguns valores para x conforme a tabela a seguir:

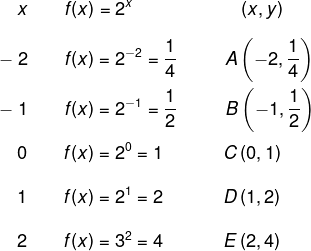
Agora que conhecemos alguns pontos da função, é possível marcá-los no plano cartesiano e traçar a curva da função exponencial.

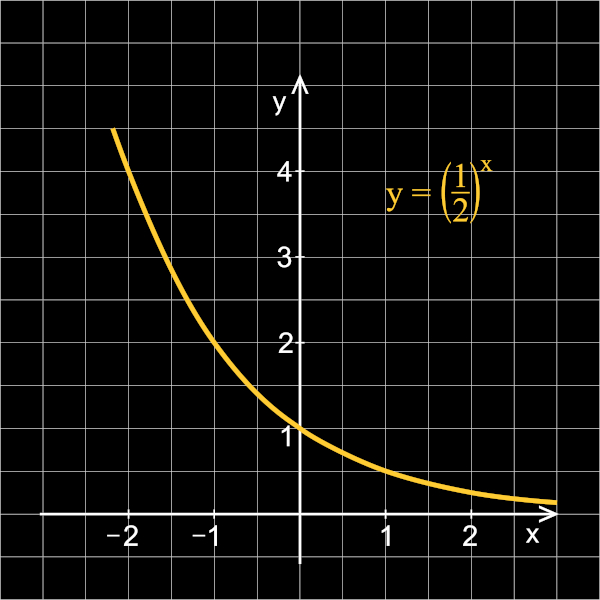
b) Construa o gráfico da função a seguir:

Nesse caso, a função é decrescente, já que a base é um número entre 0 e 1, então o gráfico será decrescente.

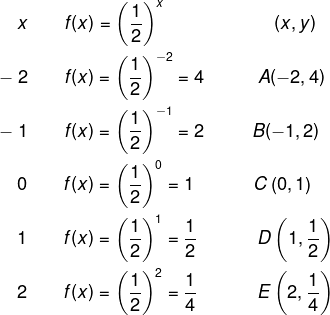
Após encontrar alguns valores numéricos, é possível representar no plano cartesiano o gráfico da função:

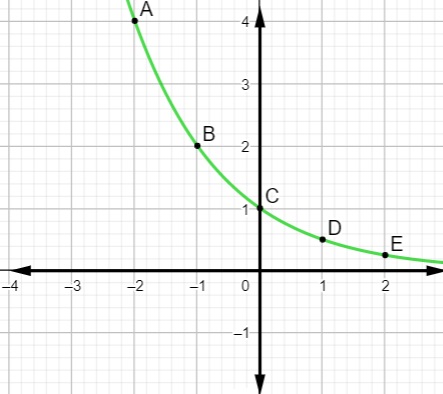
Propriedades da função exponencial

→ 1ª propriedade

Em uma função exponencial qualquer, independentemente do valor de sua base a, temos que f(0) = 1. Afinal, sabemos que essa é uma propriedade de potência, ou seja, todo número elevado a 0 é 1. Isso significa que o gráfico vai interceptar o eixo vertical no ponto (0,1) sempre.

→ 2ª propriedade

A função exponencial é injetora. Dados x₁ e x₂ tal que x₁ ≠ x₂, então as imagens também serão diferentes, ou seja, f(x₁) ≠ f(x₂), o que significa que, para cada valor da imagem, existe um único valor no domínio que corresponde a essa imagem.

Ser injetiva significa que, para valores diferentes de y, existirá um único valor de x que faz com que f(x) seja igual a y.

→ 3ª propriedade

É possível saber o comportamento da função de acordo com o valor da sua base. O gráfico será crescente se a base for maior que 1 (a > 1) e decrescente se a base for menor que 1 e menor que 0 (0 < a < 1).

→ 4ª propriedade

O gráfico da função exponencial está sempre no 1º e 2º quadrantes, pois o contradomínio da função são os reais positivos diferentes de zero.

Leia também: Como construir o gráfico de uma função?

Função exponencial e função logarítmica

Como a função exponencial é uma função que admite inversa, essa comparação entre função exponencial e função logarítmica é inevitável. Acontece que a função logarítmica é a função inversa da exponencial. Os gráficos dessas funções são simétricos em relação à bissetriz do eixo x. Ser uma função inversa significa que a função logarítmica faz o contrário do que a função exponencial faz, ou seja, na função exponencial, se f(x) = y, então a função logarítmica, por ser inversa, será denotada por f^-1 o f^-1 (y) = x.

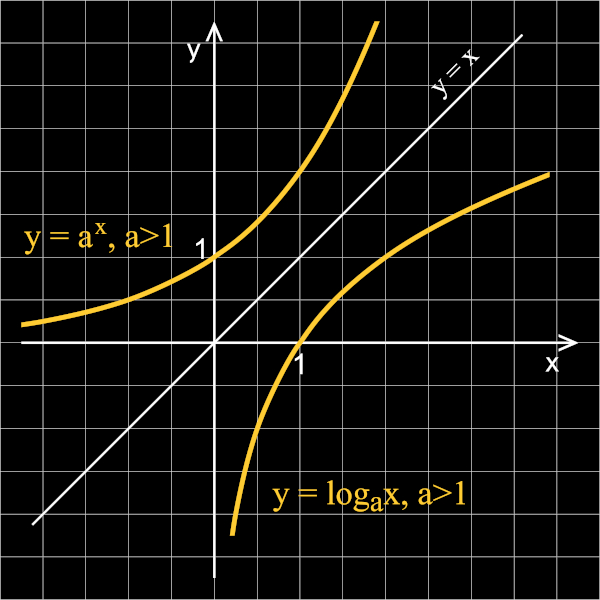
Exercícios resolvidos

(Enem 2015) O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1800·(1,03)^t.

De acordo com a proposta do sindicato, o salário de um profissional dessa empresa com 2 anos de tempo de serviço será, em reais,

a) 7.416,00

b) 3.819,24

c) 3.709,62

d) 3.708,00

e) 1909,62

Resolução:

Queremos calcular a imagem da função quando t = 2, ou seja, s(2). Substituindo t = 2 na fórmula, encontraremos que:

s(2) = 1800 · (1,03)²

s(2) = 1800 · 1,0609

s(2) = 1909,62

Alternativa E

2) (Enem 2015) O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8 000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50%. Estima-se que esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50%. Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria.

Se a estimativa for alcançada, qual é a expressão que determina o número de unidades produzidas P em função de t, para t ≥ 1?

a) P(t) = 0,5 · t ^-1 + 8 000

b)P(t) = 50 · t ^-1 + 8000

c)P(t) = 4 000 · t^-1 + 8 000

d)P(t) = 8 000 · (0,5)^t-1

e)P(t) = 8 000 · (1,5)^t-1

Resolução:

Note que existe uma relação entre o ano t e a quantidade de determinado produto P. Sabendo que há um aumento de 50% para cada ano, isso significa que, ao comparar a produção de um ano anterior ao posterior, o valor do segundo corresponde a 150%, que é representado por 1,5. Sabendo que a produção inicial é 8 000 e que, no primeiro ano, essa foi a produção, podemos descrever essa situação por:

• No primeiro ano, ou seja, se t= 1 → s(t) = 8 000.

• No segundo ano, se t = 2 → P(2) = 8 000 · 1,5.

• No terceiro ano, se t = 3 → P(3) = 8 000 · 1,5 · 1,5 = 8 000 · 1,5².

• Ao passar t anos, teremos P(t) = 8 000 · (1,5)^t-1.

Alternativa E

 

Por Raul Rodrigues de Oliveira
Professor de Matemática