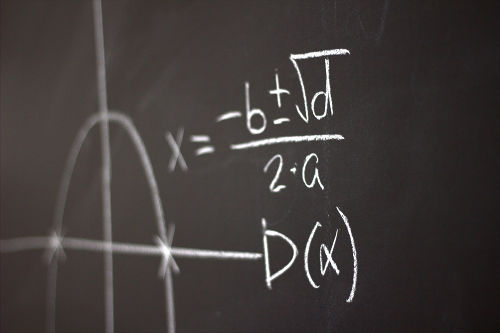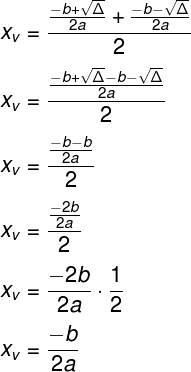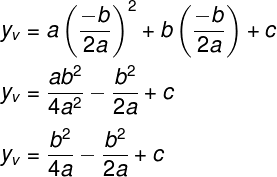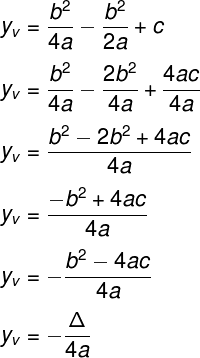Coordenadas do vértice da parábola

Uma função do segundo grau é aquela que pode ser escrita na forma f(x) = ax² + bx + c. Toda função do segundo grau é representada geometricamente por uma parábola, que é uma figura geométrica plana. As parábolas ligadas a funções do segundo grau possuem ponto de máximo ou ponto de mínimo. O maior candidato a um desses pontos é chamado de vértice da parábola.

Obtendo as coordenadas do vértice

As coordenadas do vértice podem ser obtidas de duas maneiras. A primeira utiliza uma das seguintes fórmulas:

x_v = – b
       2a

y_v = – Δ
        4a

Nessas fórmulas, x_v e y_v são as coordenadas do vértice da função do segundo grau, ou seja, V(x_v, y_v).

A segunda maneira de encontrar as coordenadas do vértice é a seguinte: suponha que x₁ e x₂ sejam as raízes de uma função do segundo grau, o ponto médio entre as raízes será a coordenada x do vértice. Sabendo disso, basta encontrar a imagem desse valor por meio da função analisada. Assim, dadas as raízes x₁ e x₂ de uma função f(x) = ax² + bx + c, temos:

x_v = x₁ + x₂
            2  

y_v = f(x_v) = ax_v² + bx_v + c

Essa é segunda técnica usada para demonstrar as fórmulas dadas.

Demonstração das fórmulas

Dada uma função do segundo grau qualquer f(x) = ax² + bx + c, com raízes x₁ e x₂, podemos encontrar a coordenada x_v calculando a média entre essas raízes. Para tanto, lembre-se de que:

x₁ = – b + √Δ
           2a 

x₂ = – b – √Δ
           2a  

Portanto:

Substituindo esse valor na função f(x) = ax² + bx + c, temos:

Fazendo o mínimo múltiplo comum dos denominadores, encontramos:

Exemplo

Encontre as coordenadas do vértice da função f(x) = x² – 16.

Usando as fórmulas, obtemos:

x_v = – b
        2a

x_v = – 0
         2

x_v = 0

y_v = – Δ
        4a

y_v = – (b² – 4·a·c)
              4a   

y_v = – (0² – 4·1·(– 16))
                  4     

y_v = – (– 4·(– 16))
                4      

y_v = – (64)
           4

y_v = – 16

As coordenadas do vértice dessa função são V (0, – 16).

Por Luiz Paulo Moreira
Graduado em Matemática