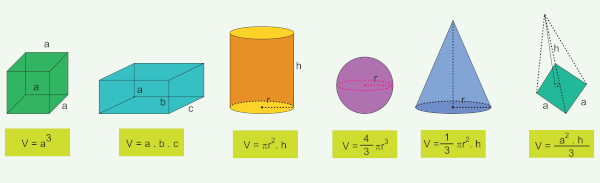
O volume de um sólido geométrico é uma grandeza que representa o espaço que esse sólido geométrico ocupa. As medidas de volume mais comuns são as unidades cúbicas, como os metros cúbicos m³, os seus múltiplos e os seus submúltiplos. Os principais sólidos geométricos são os prismas, as pirâmides, o cone, o cilindro e a esfera, e cada um deles possui fórmulas específicas para o cálculo do volume.
Leia também: Quais as diferenças entre figuras planas e espaciais?
Tópicos deste artigo
- 1 - Resumo sobre o volume dos sólidos geométricos
- 2 - Medidas de volume
- 3 - Como calcular o volume de sólidos geométricos?
- 4 - Exercícios resolvidos sobre volume dos sólidos geométricos
Resumo sobre o volume dos sólidos geométricos
-
Cada sólido geométrico possui uma fórmula diferente para o cálculo do seu volume.
-
O volume de um sólido é medido em unidades cúbicas, como metros cúbicos, centímetros cúbicos, entre outras.
-
Fórmula para calcular o volume do prisma:
V = Ab · h
-
Fórmula para calcular o volume da pirâmide:
![]()
-
Fórmula para calcular o volume de um cilindro:
V = πr² · h
-
Fórmula para calcular o volume de um cone:
![]()
-
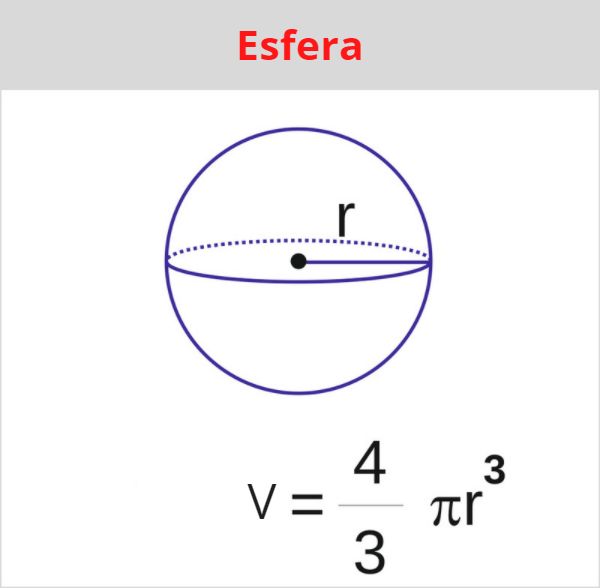
Fórmula para calcular o volume da esfera:
![]()
Medidas de volume
Chamamos de volume o espaço que um determinado sólido geométrico ocupa, logo, só faz sentido calcular o volume de objetos tridimensionais. Para medir o volume, utilizamos como unidade de medida o metro cúbico (m³) e seus múltiplos, que são:
-
decâmetro cúbico (dam³)
-
hectômetro cúbico (hm³)
-
quilômetro cúbico (km³)
Existem também os submúltiplos do metro cúbico, que são:
-
decímetro cúbico (dm³)
-
centímetro cúbico (cm³)
-
milímetro cúbico (mm³)
Veja também: Quais são as medidas de comprimento?
Como calcular o volume de sólidos geométricos?
Encontrar o volume de um sólido geométrico é fundamental para várias atividades do nosso cotidiano, por exemplo, para saber a capacidade de um galpão, para saber o espaço ocupado por um determinado móvel da nossa casa. Calculamos o volume utilizando fórmulas específicas para cada um dos sólidos geométricos. Vejamos agora as fórmulas de volume dos principais sólidos geométricos da geometria espacial.
-
Volume do prisma
Começando pelo prisma, um dos sólidos mais comuns no cotidiano. O prisma é todo sólido geométrico que possui duas bases iguais e faces laterais formadas por paralelepípedos, por exemplo, caixas de sapato, prédios, entre outros objetos.
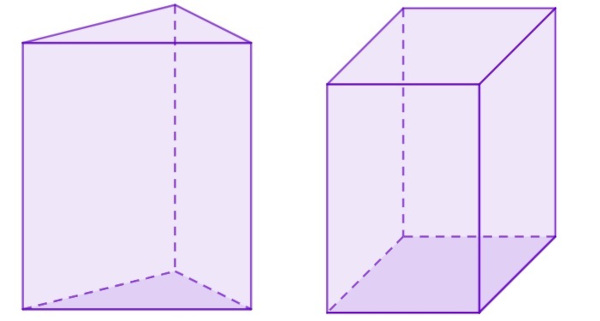
Para calcular o volume do prisma, é necessário conhecer a área da base, que pode ser formada por qualquer polígono. O volume do prisma é calculado pelo produto entre a área da base e a altura do prisma.
Vprismas = Ab · h
Ab → área da base
h → altura do prisma
Existem dois casos particulares de prisma bastante recorrentes que são o cubo e o paralelepípedo retangular.
→ Volume do cubo
Começando pelo cubo, sabemos que ele possui todas as arestas congruentes. Então, para calcular o volume do cubo, sabemos que a área do quadrado é igual ao quadrado da aresta. Para calcular o volume, multiplicamos pela altura, que, no caso do cubo, também é igual à medida da aresta. Assim, o volume do cubo é dado por:
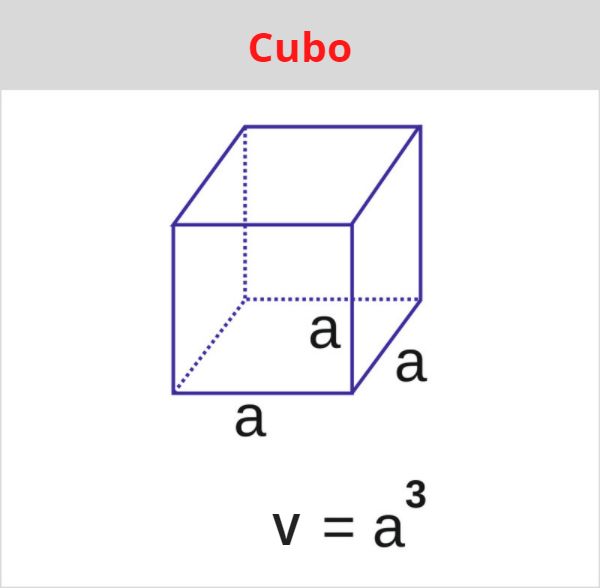
→ Volume do paralelepípedo retângulo
O volume do paralelepípedo retângulo pode ser encontrado quando multiplicamos as suas três dimensões:
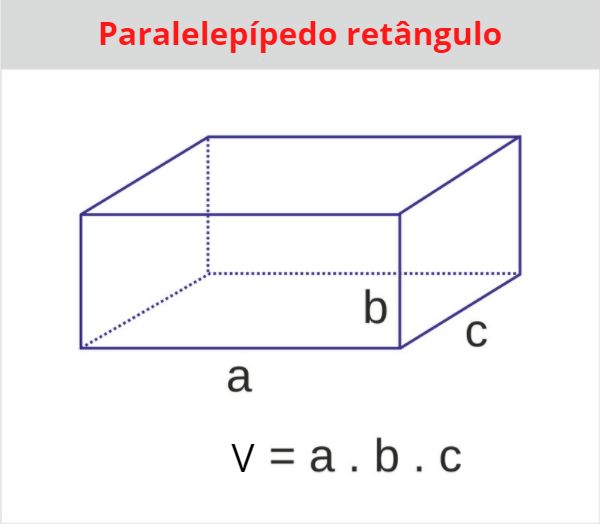
Exemplo 1:
Calcule o volume de um prisma no formato de um cubo cujas arestas medem 5 cm cada:
V = a³
V = 5³
V = 125 cm³
Exemplo 2:
Calcule o volume do prisma a seguir:
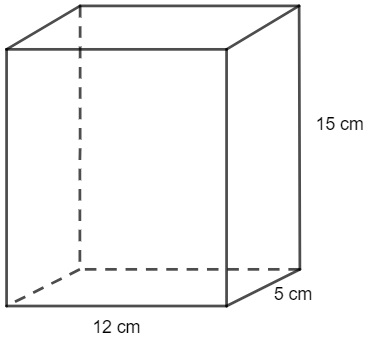
Como sua base é um retângulo, a área da base é o produto entre 12 e 5. Para encontrar o volume, multiplicaremos a área da base pela altura, então, temos que:
V = Ab · h
V = 12 · 5 · 15
V = 60 · 15
V = 900 cm³
→ Videoaula sobre volume do prisma
-
Volume da pirâmide
A pirâmide é o sólido geométrico que possui a base formada por um polígono e as faces laterias formadas por um triângulo, ligando os vértices da base a um ponto fora da base conhecido como vértice da pirâmide. Assim como o prisma, a pirâmide também pode possuir diferentes bases.
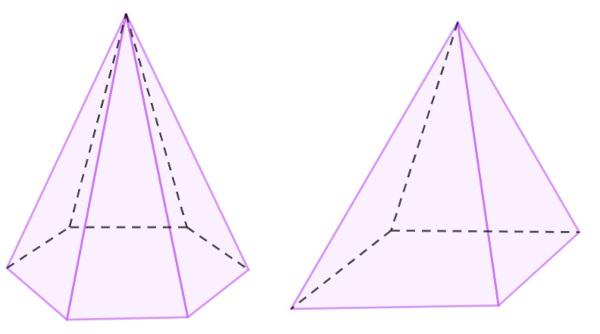
Para calcular o volume da pirâmide, é necessário calcular a área da base. O volume da pirâmide é dado pela fórmula:
![]()
Exemplo:
Calcule o volume de uma pirâmide que possui base quadrada de lados medindo 6 metros e altura de 10 metros.
Como a base da pirâmide é um quadrado, a sua área será o lado ao quadrado, então, temos que:
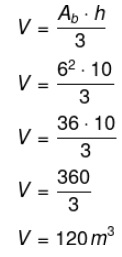
Leia também: Tronco de pirâmide – figura obtida de uma secção transversal em uma pirâmide
-
Volume do cilindro
O cilindro é o sólido geométrico que possui duas bases circulares de mesmo raio. Classificado como um corpo redondo devido a sua forma arredondada, esse sólido geométrico é bastante recorrente em embalagens como as de achocolato e de outros produtos.
Para calcular o volume de um cilindro, precisamos apenas da medida do seu raio e da sua altura:
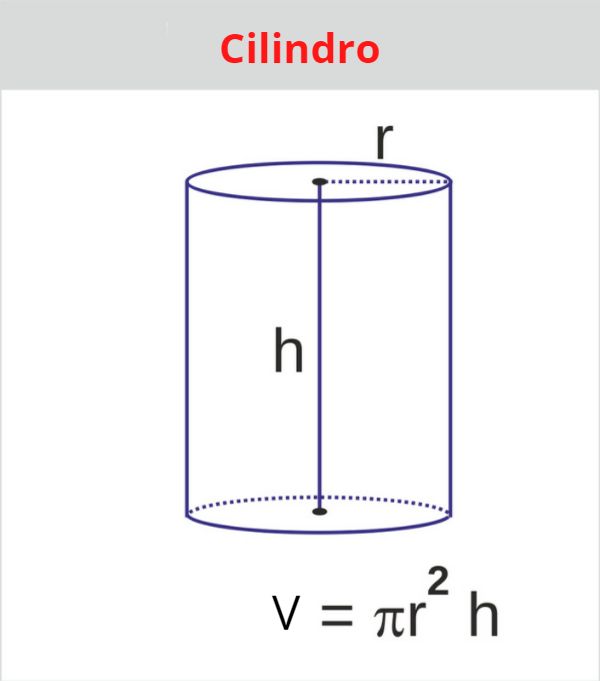
Exemplo:
Calcule o volume do cilindro a seguir (use π = 3,1):
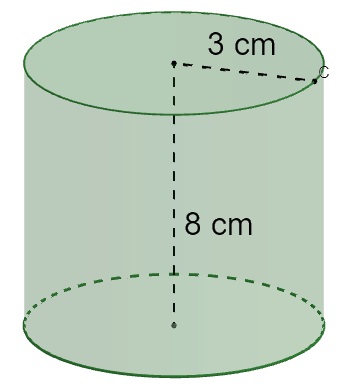
V = πr² h
V = 3,1 · 3² · 8
V = 3,1 · 9 · 8
V = 3,1 · 72
V = 223,2 cm³
→ Videoaula sobre volume do cilindro
-
Volume do cone
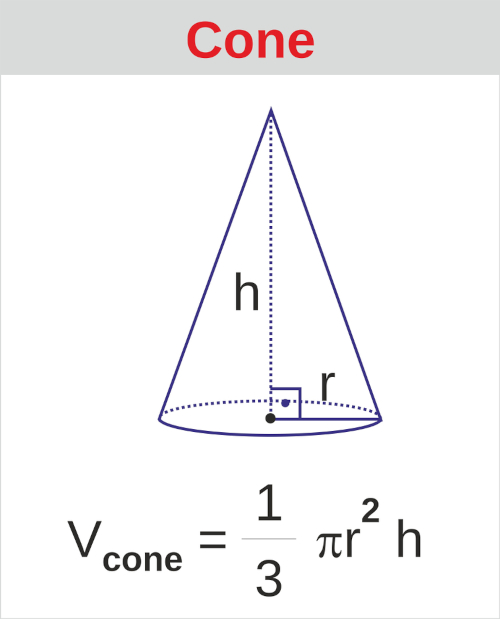
O cone também é classificado como um corpo redondo. Ele possui a base formada por um círculo e um vértice. Para calcular o volume do cone, também é necessário conhecer a sua altura e o raio de sua base:
Exemplo:
Calcule o volume do cone:
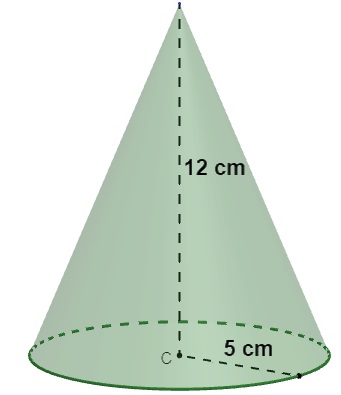
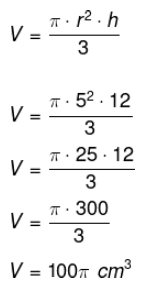
-
Volume da esfera
A esfera é também um formato comum no dia a dia, como as bolas que utilizamos para praticar certos esportes, além de ser um formato comum na natureza. Para calcular o volume da esfera, é necessário conhecer somente o seu raio:
Exemplo:
Calcule o volume da esfera que possui raio igual a 2 metros (use π = 3,1):
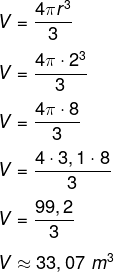
Veja também: Quais são os elementos de uma esfera?
Exercícios resolvidos sobre volume dos sólidos geométricos
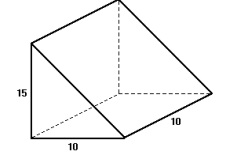
Questão 1 - (Fei) De uma viga de madeira de seção quadrada de lado L =10 cm, extrai-se uma cunha de altura h = 15 cm, conforme a figura. O volume da cunha é:
A) 250 cm³
B) 500 cm³
C) 750 cm³
D) 1000 cm³
E) 1250 cm³
Resolução
Alternativa C
Como a base é um triângulo, sabemos que:
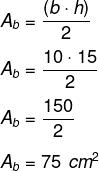
Agora calcularemos o volume do prisma:
V = Ab · h
V = 75 · 10
V = 750 cm³
Questão 2 - (FGV) O volume de uma esfera de raio r é dado por V = 4/3 π r³. Um reservatório com formato esférico tem um volume de 36 π metros cúbicos. Sejam A e B dois pontos da superfície esférica do reservatório e seja m a distância entre eles. O valor máximo de m em metros é:
A) 5,5
B) 5
C) 6
D) 4,5
E) 4
Resolução
Alternativa C
A maior distância entre dois pontos de uma esfera é o diâmetro dessa esfera. Como conhecemos o volume da esfera, então é possível calcular o seu raio:
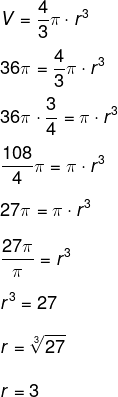
Como a maior distância possível é igual ao diâmetro, ou seja, ela mede o dobro do raio, então, d = 6.
Por Raul Rodrigues de Oliveira
Professor de Matemática