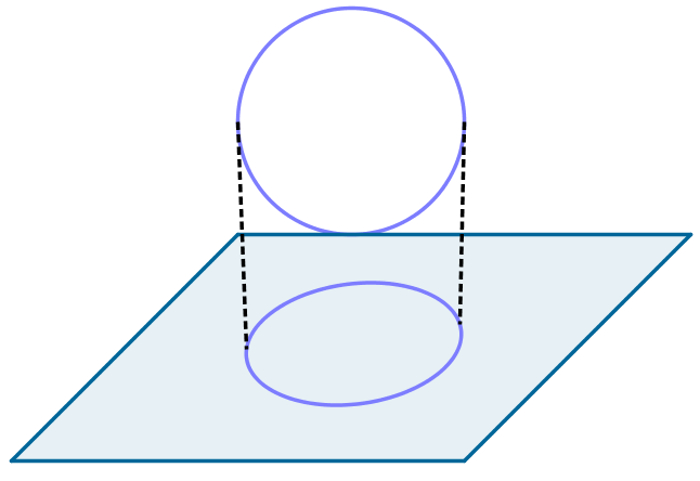
Dada uma figura geométrica qualquer e um plano que não contém nenhum de seus pontos, a projeção ortogonal dessa figura sobre o plano é a imagem formada no plano pelo pé do segmento de reta ortogonal a esse plano que liga cada ponto dessa figura ao plano. Uma projeção ortogonal, portanto, pode ser imaginada como a sombra de uma figura geométrica em um plano sob o sol do meio-dia.
Dessa maneira, perceba que nem sempre a projeção ortogonal manterá toda a forma original da figura observada. Imagine que um avião está fazendo uma manobra e fez um giro sobre o próprio eixo de 90º e, assim, suas asas ficaram na posição vertical. A sombra produzida por esse avião no solo não mostrará suas asas, embora saibamos que elas existem.
Projeção ortogonal de um ponto sobre o plano
A projeção ortogonal do ponto A sobre o plano é exatamente o ponto de encontro entre esse plano e a reta ortogonal a ele que contém o ponto A. Sendo assim, a projeção ortogonal de um ponto sobre o plano também será um ponto.

Projeção ortogonal de uma reta sobre o plano
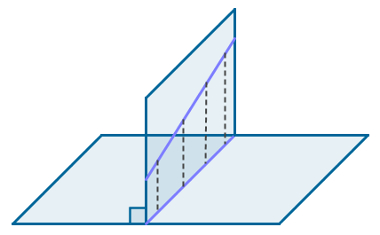
A projeção ortogonal entre uma reta r e um plano α pode ser um ponto ou outra reta. O primeiro caso ocorre quando a reta já é ortogonal ao plano, e o segundo caso ocorre quando a reta r não é ortogonal ao plano α. Assim, é necessário encontrar um segundo plano ortogonal ao primeiro que contenha a reta r. A intersecção entre esses dois planos será a projeção ortogonal da reta r sobre o plano α. Sabendo que a intersecção entre dois planos é uma reta, podemos afirmar que a projeção ortogonal entre uma reta e um plano é outra reta ou um ponto.
Projeção ortogonal de um segmento de reta sobre o plano
Essa projeção ortogonal também pode ser um ponto ou outro segmento de reta. Nesse caso, o que muda entre a reta e sua projeção ortogonal ou entre o segmento de reta e sua projeção ortogonal é o ângulo que eles formam com o plano. A projeção ortogonal sempre forma o ângulo 0°, e a reta ou segmento inicial forma um ângulo qualquer.
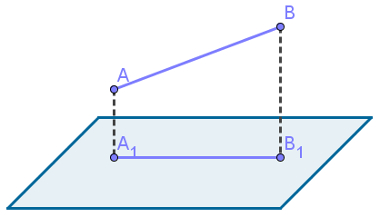
Se o segmento de reta já for ortogonal ao plano, a sua projeção ortogonal será apenas um ponto. Se o segmento de reta não for ortogonal ao plano, sua projeção ortogonal será o segmento de reta cujas extremidades são as projeções de suas extremidades sobre o plano. Observe isso na figura a seguir:
Projeção ortogonal de uma figura geométrica
Dado o plano α e a figura A, a projeção ortogonal de A sobre α será o conjunto de pontos formado pelas projeções ortogonais de todos os pontos de A sobre α.
É necessário usar a imaginação para observar projeções ortogonais. No caso dessas figuras, é bom pensar no formato que teria sua sombra ao meio-dia em um solo plano.
O exemplo seguinte demonstra o último tipo de projeção ortogonal, que é aquele em que é preciso imaginar a trajetória descrita por pontos e objetos para pensar em sua projeção. Observe:
Exemplo:
(ENEM 2013) – Gangorra é um brinquedo que consiste de uma tábua longa e estreita equilibrada e fixada em seu ponto central (pivô). Nesse brinquedo, duas pessoas sentam-se nas extremidades e, alternadamente, impulsionam-se para cima, fazendo descer a extremidade oposta, realizando assim o movimento da gangorra. Considere a gangorra representada na figura, em que os pontos A e B são equidistantes do pivô:
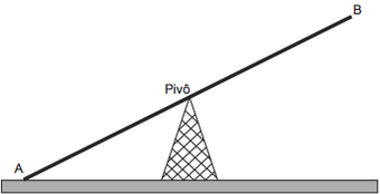
A projeção ortogonal da trajetória dos pontos A e B, sobre o plano do chão da gangorra, quando esta se encontra em movimento, é:
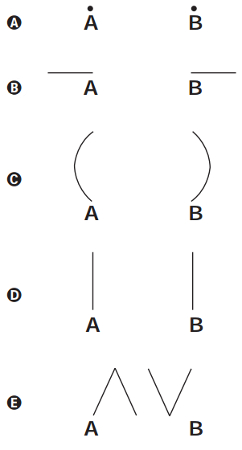
Observe que a trajetória dos pontos A e B são partes de uma circunferência. Para quem olha de cima, o ponto B, por exemplo, move-se em linha reta para trás e, depois, para frente. Para quem está de frente para essa gangorra, essa trajetória seria como na letra C da questão. Entretanto, a projeção ortogonal é o movimento equivalente à trajetória vista por cima.
Gabarito: letra B.
Por Luiz Paulo Moreira
Graduado em Matemática