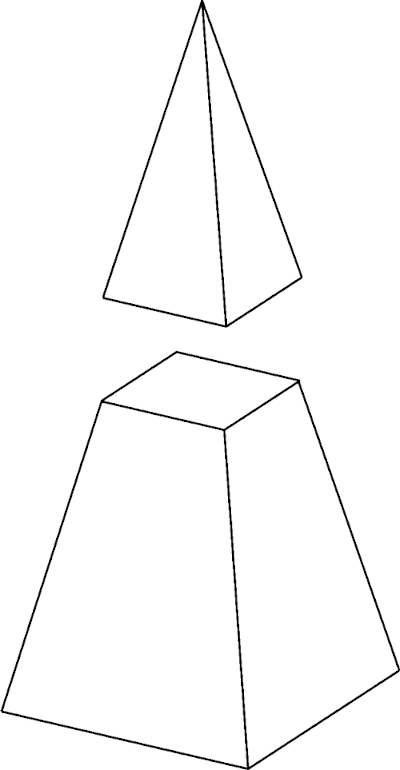
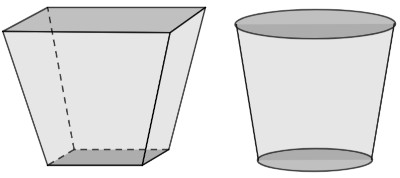
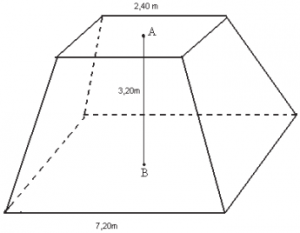
Tronco de pirâmide

Tronco de pirâmide é o sólido geométrico encontrado na parte inferior da pirâmide quando nela é realizada uma secção transversal, a qualquer altura. A secção transversal é um corte feito por um plano paralelo à base do sólido geométrico. Quando é feita a secção transversal, formam-se dois sólidos geométricos: um deles é uma pirâmide menor e o outro, o tronco de pirâmide.

O tronco de pirâmide possui como principais elementos a base menor, a base maior e a altura, que são úteis para o cálculo de seu volume e área total. Para realizar tais cálculos, utilizam-se fórmulas específicas.

Leia também: Como se calcula a área da pirâmide?

Tópicos deste artigo

• 1 - Resumo sobre tronco de pirâmide
• 2 - Elementos do tronco de pirâmide
• 3 - Área de um tronco de pirâmide
  • → Videoaula sobre área de tronco de pirâmide
• 4 - Volume do tronco de pirâmide
  • → Videoaula sobre volume de tronco de pirâmide
• 5 - Exercícios resolvidos sobre tronco de pirâmide

Resumo sobre tronco de pirâmide

• O tronco de pirâmide é o sólido obtido da parte inferior de uma pirâmide quando realizada uma secção transversal.

• Para calcular a área total do tronco de pirâmide, somamos as suas áreas laterias e as áreas das bases maior e menor.

  A_T = A_B + A_b + A_l

• O cálculo do volume do tronco de pirâmide é dado pela fórmula:

Elementos do tronco de pirâmide

O tronco de pirâmide é o sólido geométrico obtido pela secção transversal de uma pirâmide qualquer, a qualquer altura.

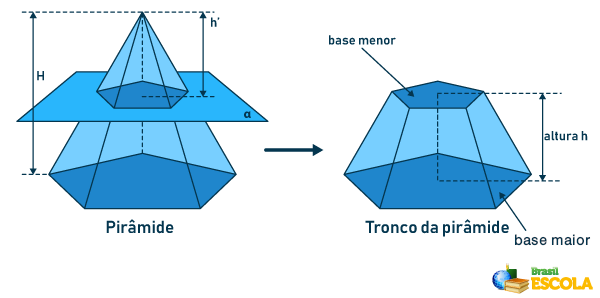
Como todo sólido geométrico, o tronco de pirâmide possui elementos importantes:

• altura;

• base maior;

• base menor.

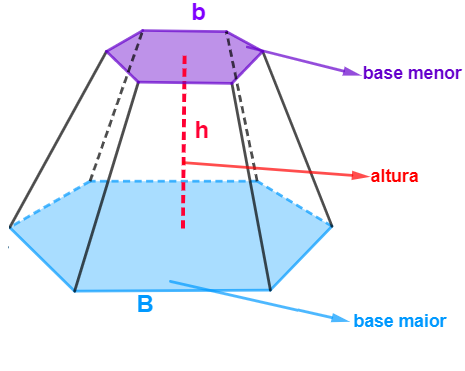
• B → base maior;

• b → base menor;

• h → comprimento da altura.

Observação:

Note que a base maior e a base menor sempre são compostas por polígonos semelhantes, podendo ser triângulos, quadrados, retângulos, pentágonos, hexágonos ou qualquer outro polígono. Além disso, as faces laterais de um tronco de pirâmide são sempre trapézios.

Leia também: Tronco de cone — sólido formado pela secção transversal de um cone

Área de um tronco de pirâmide

A área total do tronco de pirâmide é a soma das áreas da base com a área lateral.

A_T = A_B + A_b + A_l

• A_T → área total do tronco de pirâmide;

• A_B → área da base maior;

• A_b → área da base menor;

• A_l → área lateral, encontrada pela soma das áreas dos trapézios que compõem o sólido.

→ Videoaula sobre área de tronco de pirâmide

Volume do tronco de pirâmide

Para calcular o volume de um tronco de pirâmide, é comum calcular a diferença entre o volume da pirâmide maior e o volume da pirâmide menor quando realizada a secção transversal. Existe também uma fórmula específica para calcular o volume de um tronco de pirâmide:

• V → volume;

• h → altura do tronco;

• A_B → área da base maior;

• A_b → área da base menor.

→ Videoaula sobre volume de tronco de pirâmide

Exercícios resolvidos sobre tronco de pirâmide

Questão 1

(Enem 2020) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são

A) 2 quadrados e 4 retângulos.

B) 1 retângulo e 4 triângulos isósceles.

C) 2 quadrados e 4 trapézios isósceles.

D) 1 quadrado, 3 retângulos e 2 trapézios retângulos.

E) 2 retângulos, 2 quadrados e 2 trapézios retângulos.

Resolução:

Alternativa C

Primeiramente, faremos a representação do tronco de uma pirâmide de base quadrada.

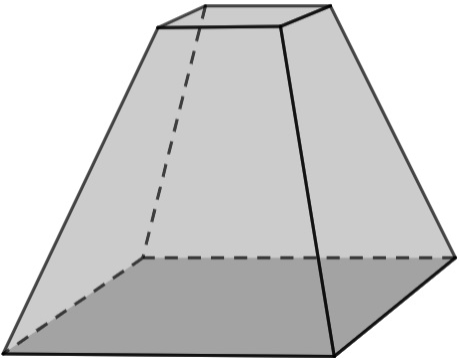
Analisando esse sólido geométrico, é possível perceber que as suas bases (face superior e face inferior) são formadas por 2 quadrados. Além disso, ele é composto por 4 faces laterais que são todas no formato de trapézio. Como as arestas que formam os lados oblíquos dos trapézios são congruentes, então há 4 trapézios isósceles. Dessa forma, há 2 quadrados e 4 trapézios isósceles.

Questão 2

(Enem 2009) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.

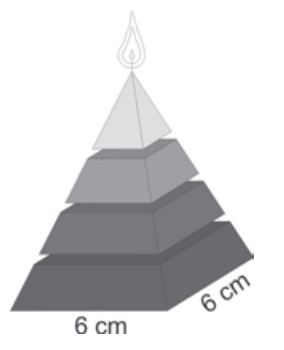
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?

A) 156 cm³.

B) 189 cm³.

C) 192 cm³.

D) 216 cm³.

E) 540 cm³.

Resolução:

Alternativa B

Para encontrar o volume do tronco de pirâmide que forma a nova vela, calcularemos a diferença entre o volume da pirâmide maior e o volume da pirâmide menor.

Perceba que há 1 cm de distância entre os blocos, então a altura da pirâmide maior é 19 – 3 = 16 cm. A pirâmide maior tem 6 cm de lado da base. Como a base é um quadrado, então A_b = l² + 6² = 36.

Calculando o volume da pirâmide maior, obtém-se o seguinte:

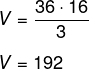
A altura da pirâmide menor na parte superior é de 16 : 4 = 4 cm. A aresta é de 6 : 4 = 1,5 cm. Portanto, a área da base da pirâmide menor é de 1,5² = 2,25 cm².

Calculando o volume:

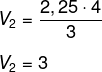
A diferença entre os volumes é de 192 – 3 = 189 cm³

Por Raul Rodrigues de Oliveira
Professor de Matemática