O volume da esfera é o espaço ocupado por esse sólido geométrico. Por meio do raio da esfera — ou seja, da distância entre o centro e a superfície — é possível calcular seu volume.
Leia também: Volume de sólidos geométricos
Tópicos deste artigo
- 1 - Resumo sobre o volume da esfera
- 2 - Videoaula sobre o volume da esfera
- 3 - O que é esfera?
- 4 - Fórmula do volume da esfera
- 5 - Como calcular o volume da esfera?
- 6 - Regiões da esfera
- 7 - Outras fórmulas da esfera
- 8 - Exercícios resolvidos sobre o volume da esfera
Resumo sobre o volume da esfera
-
A esfera é um corpo redondo obtido pela revolução de um semicírculo em torno de um eixo que contém o diâmetro.
-
Todos os pontos de uma esfera estão a uma distância igual ou menor que r do centro da esfera.
-
O volume da esfera depende da medida do raio.
-
A fórmula do volume da esfera é \(V=\frac{4·π·r^3}3\)
Videoaula sobre o volume da esfera
O que é esfera?
Considere um ponto O no espaço e um segmento com medida r. A esfera é o sólido formado por todos os pontos que estão a uma distância igual ou inferior a r de O. Denominamos O de centro da esfera e r de raio da esfera.
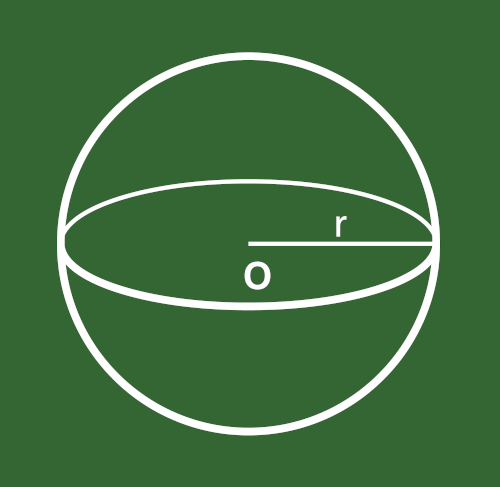
A esfera também pode ser caracterizada como um sólido de revolução. Observe que a rotação de um semicírculo em torno de um eixo que contém seu diâmetro forma uma esfera:

Fórmula do volume da esfera
Para calcular o volume V de uma esfera, utilizamos a fórmula abaixo, em que r é raio da esfera:
\(V=\frac{4·π·r^3}{3}\)
É importante observar a unidade de medida do raio para determinar a unidade de medida do volume. Por exemplo, se r está indicado em cm, então o volume deve ser indicado em cm³.
Como calcular o volume da esfera?
O cálculo do volume da esfera depende apenas da medida do raio. Vejamos um exemplo.
Exemplo: Utilizando a aproximação π = 3, determine o volume de uma bola de basquete com 24 centímetros de diâmetro.
Como o diâmetro corresponde ao dobro do raio, r = 12 cm. Aplicando a fórmula do volume da esfera, temos que
\(V=\frac{4·π·12^3}3\)
\(V=\frac{4 · π·1728}3\)
\(V=6 912\ cm^3\)
Regiões da esfera
Considere uma esfera com centro O e raio r. Assim, podemos considerar três regiões dessa esfera:
-
A região interna é formada pelos pontos cuja distância ao centro é inferior ao raio. Se P pertence à região interna da esfera, então
\(D(P,O)<r\)
-
A região da superfície é formada pelos pontos cuja distância ao centro é igual ao raio. Se P pertence à região da superfície da esfera, então
\(D(P,O)=r\)
-
A região externa é formada pelos pontos cuja distância ao centro é superior ao raio. Se P pertence à região interna da esfera, então
\(D(P,O)>r\)
Consequentemente, os pontos da região externa da esfera não pertencem à esfera.
Saiba mais: Calota esférica — sólido obtido quando uma esfera é interceptada por um plano
Outras fórmulas da esfera
A área da esfera — ou seja, a medida de sua superfície — também possui uma fórmula conhecida. Se r é o raio da esfera, sua área A é calculada por
\(A=4·π·r^2\)
Nesse caso, também é importante observar a unidade de medida do raio para indicar a unidade de medida da área. Por exemplo, se r está em cm, então A deve estar em cm².
Exercícios resolvidos sobre o volume da esfera
Questão 1
Qual o raio de uma esfera que possui 108 centímetros cúbicos de volume? (Utilize π = 3).
a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm
e) 6 cm
Resolução
Alternativa B.
Considere que r é o raio da esfera. Sabendo que V = 108, podemos utilizar a fórmula do volume da esfera:
\(V=\frac{4·π·r^3}3\)
\(108=\frac{4·3·r^3}3\)
\(108=4·r^3\)
\(r^3=27\)
\(r = 3\ cm\)
Questão 2
Um antigo reservatório esférico possui 20 metros de diâmetro e volume V1. Deseja-se construir um segundo reservatório, de volume V2, com o dobro do volume do reservatório antigo. Assim, V2 é igual a
a) \(\frac{3000·π}{8} m^3\)
b) \(\frac{3000·π}{4} m^3\)
c) \(\frac{2000·π}{3} m^3\)
d) \(\frac{4000·π}{3} m^3\)
e) \(\frac{8000·π}{3} m^3\)
Resolução
Alternativa E.
Como o diâmetro é dobro do raio, o reservatório antigo possui raio r = 10 metros. Portanto
\(V_1=\frac{4·π·r^3}3\)
\(V_1=\frac{4·π·10^3}3\)
\(V_1=\frac{4000·π}3\ m^3\)
Pelo enunciado, \(V_2=2·V_1\), ou seja
\(V_2=\frac{8000·π}3 m^3\)
Por Maria Luiza Alves Rizzo
Professora de Matemática

