O cubo, conhecido também como hexaedro, é um sólido geométrico que possui seis faces, todas elas formadas por quadrados. Além das 6 faces, o cubo possui 12 arestas e 8 vértices. Estudado na Geometria Espacial, o cubo possui todas as suas arestas congruentes e perpendiculares, logo ele é classificado como um poliedro regular. Podemos perceber a presença do formato de cubo no nosso cotidiano, em dados comuns utilizados em jogos, embalagens, caixas, entre outros objetos.
Leia também: Pirâmide — sólido geométrico que possui todas as suas faces formadas por triângulos
Tópicos deste artigo
- 1 - Resumo sobre cubo
- 2 - O que é cubo?
- 3 - Elementos da composição do cubo
- 4 - Planificação do cubo
- 5 - Fórmulas do cubo
- 6 - Exercícios resolvidos sobre cubo
Resumo sobre cubo
-
O cubo é conhecido também como hexaedro, por possuir 6 faces.
-
O cubo é composto por 6 faces, 12 arestas e 8 vértices.
-
O cubo possui todas as suas faces formadas por quadrados, logo suas arestas são congruentes, e por isso ele é um poliedro regular, conhecido também como sólido de Platão.
-
A área da base do cubo é igual à área de um quadrado. Sendo a a medida da aresta, para calcular a área da base, temos que:
\(A_b=a^2\)
-
A área lateral do cubo é formada por 4 quadrados de lados medindo a, então para calculá-la, utilizamos a fórmula:
Anuncie aqui
\(A_l=4a^2\)
-
Para calcular a área total do cubo, basta somar a área das suas duas bases com a área lateral. Assim, utilizamos a fórmula:
\(A_T=6a^2\)
-
O volume do cubo é calculado pela fórmula:
\(V=a^3\)
-
A medida da diagonal lateral do cubo é calculada pela fórmula:
Anuncie aqui
\(b=a\sqrt2\)
-
A medida da diagonal do cubo é calculada pela fórmula:
\(d=a\sqrt3\)
O que é cubo?
O cubo é um sólido geométrico composto por 12 arestas, 8 vértices e 6 faces. Devido ao fato de ele possuir 6 faces, o cubo é conhecido também como hexaedro.

Elementos da composição do cubo
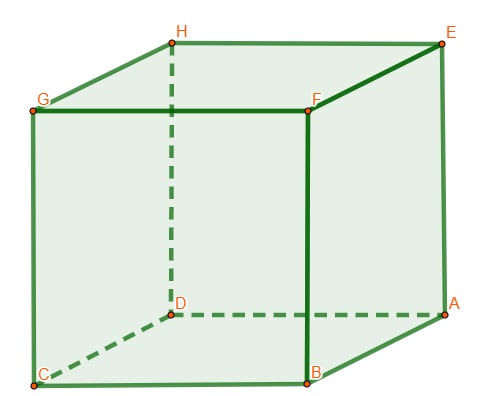
Sabendo que o cubo possui 12 arestas, 8 vértices e 6 faces, veja a imagem a seguir.
-
A, B, C, D, E, F, G e H são os vértices do cubo.
Anuncie aqui -
\(\overline{AB},\ \overline{AD},\ \overline{AE},\ \overline{BC},\ \overline{BF},\ \overline{CD,\ }\overline{CG},\ \overline{DH,\ }\overline{HG},\ \overline{EH}\overline{,\ EF},\ \overline{FG}\) são as arestas do cubo.
-
ABCD, ABFE, BCFG, EFGH, ADHE, CDHG são as faces do cubo.
O cubo é composto por 6 faces quadradas, logo todas as suas arestas são congruentes. Pelo fato de suas arestas possuírem uma mesma medida, o cubo é classificado como um poliedro regular ou sólido de Platão, junto do tetraedro, octaedro, icosaedro e dodecaedro.
Planificação do cubo
Para calcular a área do cubo, é importante analisarmos sua planificação. A planificação do cubo é composta por 6 quadrados, todos congruentes entre si:
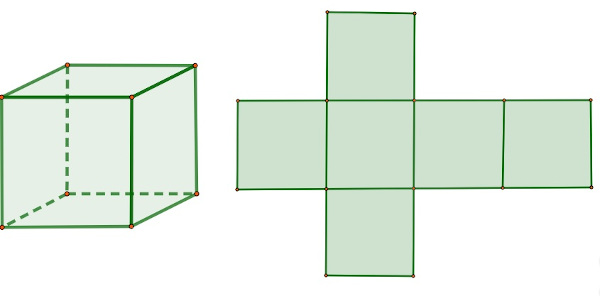
O cubo é composto por 2 bases quadradas, e a sua área lateral é composta por 4 quadrados, todos congruentes.
Veja também: Planificação dos principais sólidos geométricos
Fórmulas do cubo
Para calcular a área da base, a área lateral, a área total e o volume do cubo, consideraremos o cubo com aresta medindo a.
-
Área da base de um cubo
Como a base é formada por um quadrado de aresta a, a área da base do cubo é calculada pela fórmula:
\(A_b=a^2\)
Exemplo:
Calcule a medida da base de um cubo que possui aresta medindo 12 cm:
Resolução:
\(A_b=a^2\)
\(A_b={12}^2\)
\(A_b=144\ cm^2\)
-
Área lateral do cubo
A área lateral do cubo é composta por 4 quadrados, todos com lados medindo a. Dessa forma, para calcular a área lateral do cubo, a fórmula é:
\(A_l=4a^2\)
Exemplo:
Qual é a área lateral de um cubo que possui aresta medindo 8 cm?
Resolução:
\(A_l=4a^2\)
\(A_l=4\cdot8^2\)
\(A_l=4\cdot64\)
\(A_l=256\ cm^2\)
-
Área total do cubo
A área total do cubo ou simplesmente área do cubo é a soma da área de todas as faces do cubo. Sabemos que ele possui, ao todo, 6 lados, formados por quadrados de lado a, então a área total do cubo é calculada por:
\(A_T=6a^2\)
Exemplo:
Qual é a área total de um cubo cuja aresta mede 5 cm?
Resolução:
\(A_T=6a^2\)
\(A_T=6\cdot5^2\)
\(A_T=6\cdot25\)
\(A_T=150\ cm^2\)
-
Volume do cubo
O volume de um cubo é a multiplicação da medida das suas três dimensões. Como elas possuem todas a mesma medida, temos que:
\(V=a^3\)
Exemplo:
Qual é o volume de um cubo que possui aresta medindo 7 cm?
Resolução:
\(V=a^3\)
\(V=7^3\)
\(V=343\ cm^3\)
-
Diagonais do cubo
No cubo podemos traçar a diagonal lateral, ou seja, a diagonal da sua face, e a diagonal do cubo.
◦ Diagonal lateral do cubo
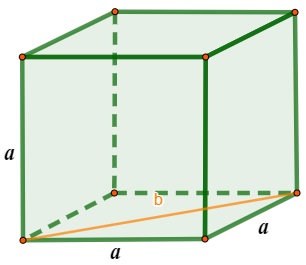
A diagonal lateral ou diagonal de uma face do cubo é indicada pela letra b na imagem. Pelo teorema de Pitágoras, temos um triângulo retângulo de catetos medindo a e hipotenusa medindo b:
b² = a² + a²
b² = 2a²
b = \(\sqrt{2a^2}\)
b = \(a\sqrt2\)
Logo, a fórmula para calcular a diagonal de uma face do cubo é:
\(b=a\sqrt2\)
◦ Diagonal do cubo
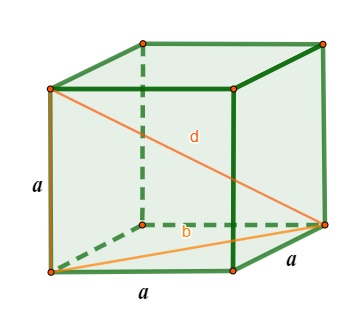
A diagonal d do cubo pode ser calculada utilizando o teorema de Pitágoras também, pois temos um triângulo retângulo de catetos b, a e hipotenusa medindo d:
\(d^2=a^2+b^2\)
Mas sabemos que b = \(a\sqrt2\):
\(d^2=a^2+\left(a\sqrt2\right)^2\)
\(d^2=a^2+a^2\cdot2\)
\(d^2=a^2+2a^2\)
\(d^2=3a^2\)
\(d=\sqrt{3a^2}\)
\(d=a\sqrt3\)
Então, para calcular a diagonal do cubo, utilizamos a fórmula:
\(d=a\sqrt3\)
Saiba mais: Cilindro — um sólido geométrico que se classifica como corpo redondo
Exercícios resolvidos sobre cubo
Questão 1
A soma das arestas de um cubo é igual a 96 cm, então a medida da área total desse cubo é:
A) 64 cm²
B) 128 cm²
C) 232 cm²
D) 256 cm²
E) 384 cm²
Resolução:
Alternativa E
Primeiramente, calcularemos a medida da aresta do cubo. Como ele possui 12 arestas e sabemos que a soma das 12 arestas é 96, temos que:
a = 96 : 12
a = 8 cm
Sabendo que cada aresta mede 8 cm, agora é possível calcular a área total do cubo:
\(A_T=6a^2\)
\(A_T=6\cdot8^2\)
\(A_T=6\cdot64\)
\(A_T=384\ cm^2\)
Questão 2
Um reservatório de água precisa ser esvaziado para higienização. Sabendo que ele possui formato de um cubo com aresta de 2 m e que 70% desse reservatório já está vazio, então o volume desse reservatório que ainda está ocupado é de:
A) 1,7 m³
B) 2,0 m³
C) 2,4 m³
D) 5,6 m³
E) 8,0 m³
Resolução:
Alternativa C
Primeiramente, calcularemos o volume:
\(V=a^3\)
\(V=2^3\)
\(V=8\ m^3\)
Se 70% do volume está vazio, então 30% do volume está ocupado. Calculando 30% de 8:
\(0,3\cdot8=2,4\ m^3\)
Por Raul Rodrigues de Oliveira
Professor de Matemática

