Cone

Chamamos de cone um sólido geométrico, também conhecido como um corpo redondo ou sólido de revolução, que possui a base circular e é construído a partir da rotação de um triângulo. O cone e os demais sólidos geométricos são objetos de estudo da geometria espacial. De acordo com as suas características, ele pode ser classificado como:

• cone reto;

• cone oblíquo;

• cone equilátero.

Há fórmulas específicas para o cálculo da área total e do volume do cone.

Leia também: O que são formas geométricas?

Tópicos deste artigo

• 1 - Elementos do cone
• 2 - Classificação de cones
  • Cone oblíquo
  • Cone reto
  • Cone equilátero
• 3 - Fórmulas do cone
  • Fórmula do volume do cone
  • Fórmula da área total do cone
• 4 - Tronco de cone
• 5 - Exercícios resolvidos sobre cone

Elementos do cone

O cone é um sólido geométrico conhecido como sólido de revolução. Bastante presente no nosso cotidiano, ele é conhecido como sólido de revolução por ser construído a partir da rotação de um triângulo.

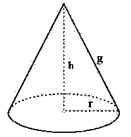
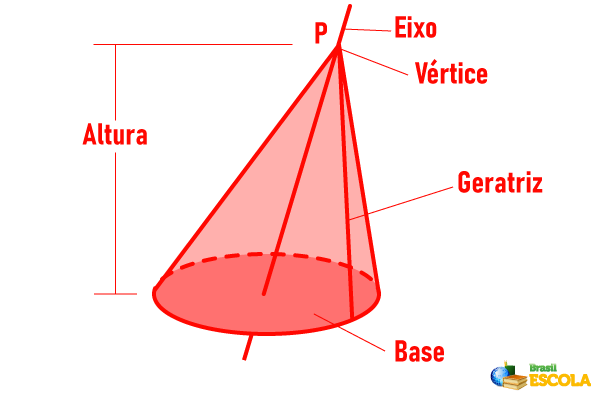
A base dele é sempre uma circunferência. Além da base em si, outro elemento importante é o raio r da circunferência, conhecido como raio da base do cone. Além disso, há o vértice do cone (V) e a altura (h), que, por definição, é o segmento que sai do vértice e é perpendicular à base, ou seja, forma um ângulo de 90º.

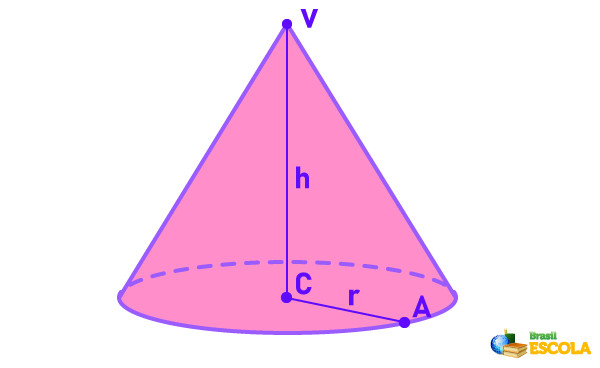
Além dos elementos já citados, existe outro elemento importante no cone, que é a geratriz. Chamamos de geratriz do cone qualquer segmento que parte do vértice e vai de encontro à circunferência da base.

A geratriz é o segmento de reta AV na imagem. Note que ele é a hipotenusa do triângulo AVC, logo podemos estabelecer uma relação pitagórica entre o raio, a altura e a geratriz.

g² = r² + h²

g → geratriz do cone

r→ raio da base

h→ altura

Veja também: Quais são as aplicações do teorema de Pitágoras?

Classificação de cones

De acordo com as suas características, podemos classificar o cone em dois casos: reto ou oblíquo. Como caso particular de cone reto, há os cones equiláteros.

• Cone oblíquo

Um cone é conhecido como oblíquo quando o segmento que liga o vértice com o centro da sua base não coincide com a altura do cone.

Quando o vértice não está alinhado com o centro da base, o segmento que liga o vértice ao centro da circunferência não é mais a altura como no cone reto. Note que o eixo do cone, na imagem, não é perpendicular à base. Nesse caso suas geratrizes não são todas congruentes, logo não é possível encontrar o seu comprimento pelo teorema de Pitágoras, não existindo fórmulas específicas para a geratriz nem para o volume e a sua área toral.

• Cone reto

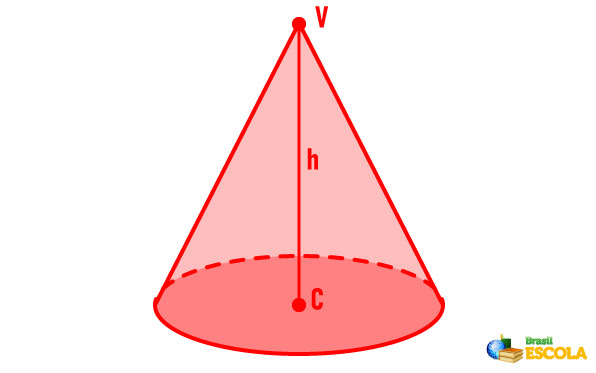
O cone é conhecido como reto quando seu eixo coincide com a altura do cone, ou seja, o segmento que liga o vértice ao centro da circunferência da base é perpendicular ao plano que contém a base do cone.

• Cone equilátero

Um cone reto é conhecido como equilátero quando o seu diâmetro é igual à sua geratriz.

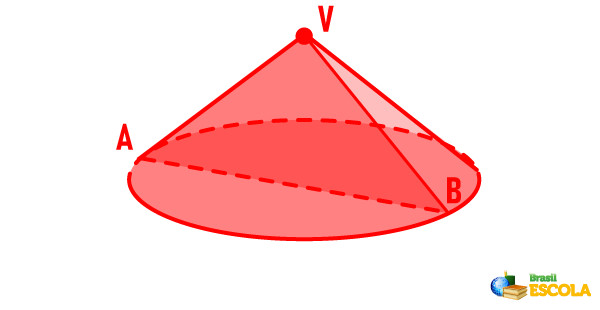
Note que o triângulo AVB é um triângulo equilátero, ou seja, todos os lados são congruentes, o que significa que a sua geratriz é congruente ao diâmetro da base e que, por consequência, o comprimento da geratriz é igual a duas vezes o comprimento do raio da base.

Acesse também: Cônicas – figuras formadas pela intersecção de um plano e um cone duplo

Fórmulas do cone

Ao estudar os sólidos geométricos, há dois cálculos importantes para cada um deles, que é o cálculo do volume e o cálculo da área total do sólido geométrico. Para calcular o valor do volume do cone de cada um deles, é necessário utilizar fórmulas específicas. Vale lembrar que essas fórmulas são específicas do cone reto.

• Fórmula do volume do cone

r → raio da base

V→ volume

h → altura

• Fórmula da área total do cone

Para calcular a área total, analisando a planificação do cone, faremos a soma da área lateral com área da base de um cone.

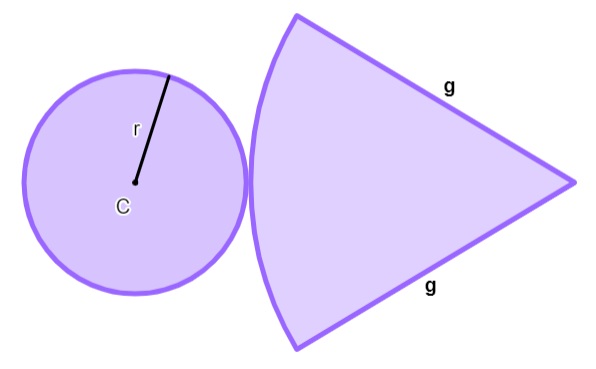
A sua base é um círculo, logo a área é calculada por:

A_b = π·r².

Já a sua área lateral é um setor circular, que é igual a: 

A_l = π·r·g

Sendo assim, a área total é igual a:

A_t =  π·r² +  π·r·g

Colocando  π·r em evidência, podemos calcular a área total por:

A_t =  π·r(r+g)

r→ raio

g → geratriz

Tronco de cone

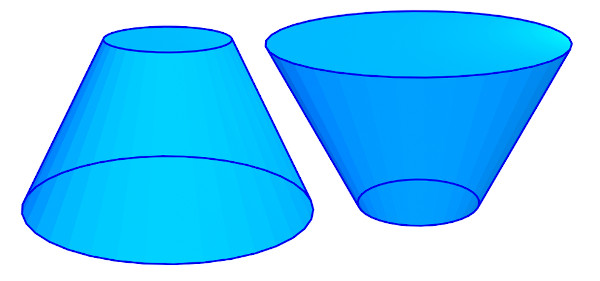
Quando se intercepta um cone por um plano paralelo à base, é possível criar o sólido geométrico conhecido como tronco de um cone. O tronco de um cone vai sempre possuir duas bases no formato de círculos, uma maior e a outra menor.

Leia também: Cilindro – sólido formado por duas bases circulares em planos distintos e paralelos

Exercícios resolvidos sobre cone

Questão 1 – (Enem 2013) Uma cozinheira, especialista em fazer bolos, utiliza uma forma no formato representado na figura:            

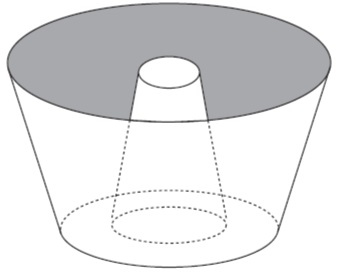
Nela identifica-se a representação de duas figuras geométricas tridimensionais. Essas figuras são:

A) um tronco de cone e um cilindro.

B) um cone e um cilindro.

C) um tronco de pirâmide e um cilindro.

D) dois troncos de cone.

E) dois cilindros.

Resolução

Alternativa D. Note que os dois sólidos possuem uma base maior e uma base maior circular, o que faz com que ambas sejam troncos de cone.

Questão 2 – Um reservatório será construído no formato de um cone, utilizando-se alumínio como material. Desprezando a espessura do reservatório e sabendo que ele é um cone reto com 1,5 m de raio e 2 m de altura, qual é a quantidade de alumínio necessária para a construção desse reservatório? (use π = 3)

A) 10 m²

B) 14 m²

C) 16 m²

D) 18 m²

E) 20 m²

Resolução

Alternativa D.

Queremos calcular a área total do cone, que é dada por:

A_t =  π·r(r+g)

Note que não temos o valor de g, então, primeiro vamos calcular o valor da geratriz g.

g² = r² + h²

g² = 1,5² + 2²

g² = 2,25+4

g² = 6,25

g = √6,25

g = 2,5 m

Então a área total será de:

A_t =  π·r(r+g)

A_t =  3·1,5(1,5+2,5)

A_t =  4,5·4

A_t =  18 m²

Por Raul Rodrigues de Oliveira
Professor de Matemática