Quando estudamos os poliedros, nos deparamos com os sólidos de Platão como caso particular. Para ser um sólido de Platão, o poliedro precisa satisfazer três condições:
-
ser convexo;
Anuncie aqui -
todas as faces possuírem a mesma quantidade de arestas;
-
todos os vértices serem extremidades de uma mesma quantidade de arestas.
Vários filósofos buscaram compreender a origem do Universo, e Platão viu na geometria espacial a explicação para essa origem. Os sólidos de Platão são:
-
tetraedro;
-
hexaedro;
-
octaedro;
Anuncie aqui -
dodecaedro;
-
icosaedro.
Todos eles são considerados polígonos regulares, já que as suas arestas e suas faces são todas congruentes. Os sólidos de Platão respeitam a relação de Euler, que relaciona o número de vértices, faces e arestas pela fórmula V + F = A + 2.
Leia também: Quais as diferenças entre as figuras planas e as espaciais?

Tópicos deste artigo
- 1 - Poliedros regulares
- 2 - Quais são os sólidos de Platão?
- 3 - Fórmula de Euler
- 4 - Exercícios resolvidos
Poliedros regulares
A busca por poliedros regulares é recorrente, pois é mais fácil trabalhar com eles. Um poliedro é classificado como regular se ele possui todas as faces formadas por um mesmo polígono congruente. Quando isso ocorre, os ângulos e arestas também são congruentes.
Os sólidos de Platão são casos particulares de poliedros regulares. O cubo, por exemplo, que é um sólido de Platão, possui todas as suas faces formadas por quadrados congruentes. Dos cinco sólidos de Platão, três são formados por faces triangulares com triângulos congruentes, um é formado por faces quadradas e o outro é formado por faces pentagonais.
Quais são os sólidos de Platão?
Platão foi um filósofo e matemático grego. Ele realizou grandes contribuições para a matemática e, na tentativa de compreender o Universo, associou os sólidos a elementos da natureza.
Para ser um sólido platônico, o poliedro precisa ser regular e convexo. Existem apenas cinco sólidos que satisfazem essa definição. São eles: o tetraedro, o cubo ou hexaedro, o octaedro, o icosaedro e o dodecaedro.
A relação feita entre o elemento da natureza e o sólido foi:
-
tetraedro – fogo
-
hexaedro – terra
-
octaedro – ar
Anuncie aqui -
icosaedro – água
-
dodecaedro – Cosmo ou Universo
Para ser um sólido de Platão, o poliedro também precisa ser convexo, todas as faces devem apresentar a mesma quantidade de arestas e todos os vértices devem ser extremidades de uma mesma quantidade de arestas.
Veja também: Paralelepípedos – sólidos geométricos formados por faces planas e poligonais
-
Tetraedro regular
O tetraedro regular é um poliedro que possui 4 faces, o que justifica o seu nome (tetra = quatro). Todas as suas faces são formadas por triângulos. Ele possui formato de uma pirâmide de base triangular e é conhecido como pirâmide de base regular, já que todas as suas faces são congruentes. Possui um total de 4 faces (em formato de triângulo equilátero), 4 vértices e 6 arestas.
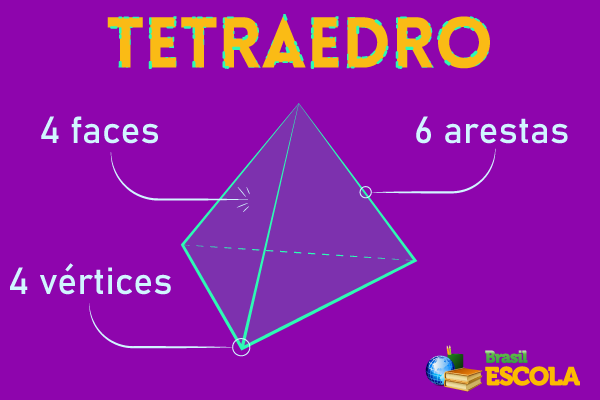
Caso você queira montar seu próprio tetraedro regular, é só baixar e imprimir o PDF.
-
Cubo ou hexaedro regular
O hexaedro regular possui 6 faces, o que justifica o seu nome (hexa = seis). As suas faces são todas quadradas. Ele é conhecido também como cubo e possui 6 faces, 12 arestas e 8 vértices.
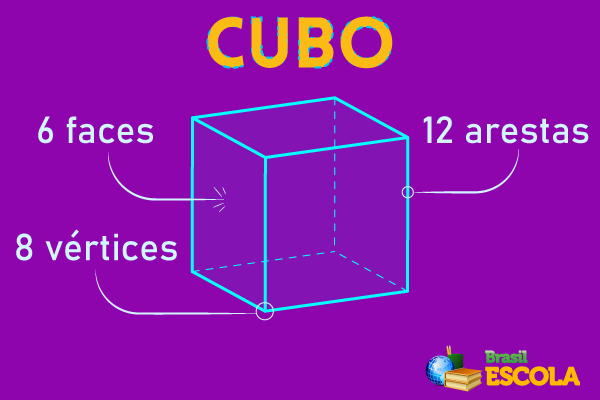
Caso você queira montar seu próprio cubo, é só baixar e imprimir o PDF.
-
Octaedro
Assim como os anteriores, o nome está ligado ao número de faces, logo o octaedro possui 8 faces. Essas faces possuem formato de triângulo equilátero. O octaedro possui 8 faces, 12 arestas e 6 vértices.
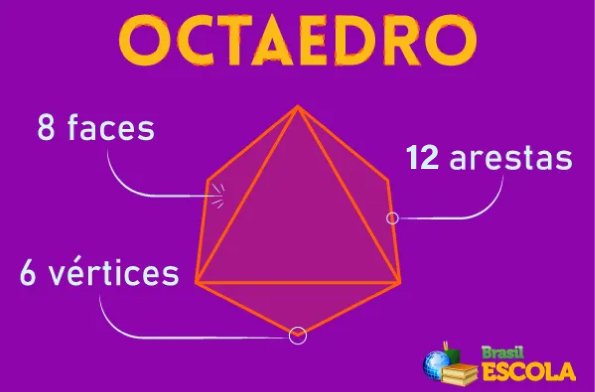
Caso você queira montar seu próprio octaedro, é só baixar e imprimir o PDF.
-
Icosaedro
O icosaedro possui um total de 20 faces. As suas faces possuem formato de triângulos equiláteros, assim como o octaedro. Ele possui um total de 20 faces, 30 arestas e 12 vértices.

Caso você queira montar seu próprio icosaedro, é só baixar e imprimir o PDF.
-
Dodecaedro
O dodecaedro é o último dos sólidos de Platão. Possui um total de 12 faces e é considerado o mais harmônico entre os cinco sólidos platônicos. Suas faces possuem formato de pentágonos. Apresenta 12 faces, 30 arestas e 20 vértices.
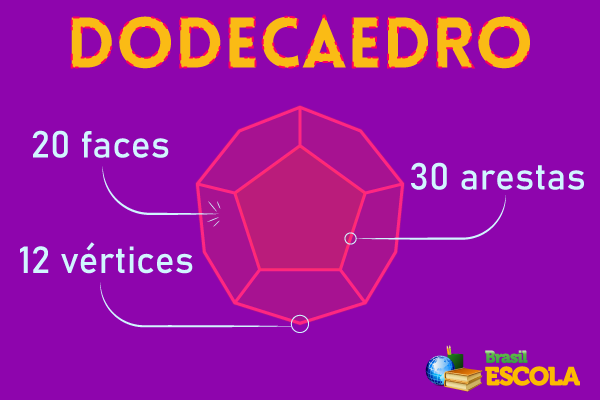
Caso você queira montar seu próprio dodecaedro, é só baixar e imprimir o PDF.
Acesse também: Cilindro – sólido geométrico formado por duas faces circulares paralelas e em planos distintos
Fórmula de Euler
Os poliedros eulerianos são os poliedros convexos. Euler desenvolveu uma fórmula que relaciona o número de faces (F), número de vértices (V) e o número de arestas (A) em um poliedro convexo. Todos os sólidos de Platão satisfazem a relação de Euler.
|
V + F = A+ 2 |
Analisando a fórmula, é possível então calcular o número de vértices a partir do número de faces e de arestas, ou o número de faces, a partir do número de vértices e arestas, enfim, conhecendo dois dos seus elementos, é sempre possível encontrar o terceiro.
-
Exemplo:
Anuncie aqui
Sabendo que um poliedro possui 8 vértices e 12 arestas e que ele é regular, qual será o número de faces que ele possui?
Sabemos que V + F = A+2
V = 8
A = 12
8 + F = 12 + 2
8 + F = 14
F = 14 – 8
F = 6
Exercícios resolvidos
Questão 1 – (Enem 2016) Os sólidos de Platão são poliedros convexos cujas faces são todas congruentes a um único polígono regular, todos os vértices têm o mesmo número de arestas incidentes e cada aresta é compartilhada por apenas duas faces. Eles são importantes, por exemplo, na classificação das formas dos cristais minerais e no desenvolvimento de diversos objetos. Como todo poliedro convexo, os sólidos de Platão respeitam a relação de Euler V - A + F = 2, em que V, A e F são os números de vértices, arestas e faces do poliedro, respectivamente.
Em um cristal, cuja forma é a de um poliedro de Platão de faces triangulares, qual é a relação entre o número de vértices e o número de faces?
A) 2V – 4F = 4
B) 2V – 2F = 4
C) 2V – F = 4
D) 2V + F = 4
E) 2V + 5F= 4
Resolução
Alternativa C. Como as faces são triangulares, sabemos que, para cada face, há 3 arestas. Porém, para relacionar o número de arestas com o número de faces, é importante lembrar que cada aresta está contida em duas faces, pois o encontro de duas faces forma uma aresta, então podemos relacionar aresta com face nesse caso por:
![]()
Tendo a relação de Euler como V – A + F = 2 e substituindo A, temos que:
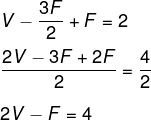
Questão 2 – Das alternativas abaixo, julgue qual delas não é um sólido de Platão.
A) Cubo
B) Tetraedro Regular
C) Icosaedro
D) Dodecaedro
E) Cone
Resolução:
Alternativa E. Das alternativas, a única que não corresponde a um sólido de Platão é o cone.




