O volume da pirâmide é calculado pela multiplicação entre a área da base e a altura, dividindo por três. Para calcular o volume da pirâmide, é necessário saber qual é o polígono que forma a base dessa pirâmide, e, por isso, para cada base, utilizamos uma fórmula diferente para encontrar a sua área. Podemos relacionar o volume do prisma com o volume de uma pirâmide de mesma altura e mesma área da base, pois o volume da pirâmide é igual a um terço do volume do prisma.
Leia também: O que são formas geométricas?
Tópicos deste artigo
- 1 - Como se calcula o volume da pirâmide?
- 2 - Pirâmide de base quadrada
- 3 - Pirâmide de base triangular
- 4 - Pirâmide de base hexagonal
- 5 - Relação entre volume da pirâmide e volume do prisma
- 6 - Exercícios resolvidos
Como se calcula o volume da pirâmide?

O volume da pirâmide pode ser calculado por uma fórmula que depende diretamente do polígono que forma a base. Para calcular o volume de uma pirâmide qualquer, utilizamos a fórmula a seguir:
![]()
V → volume
Ab → área da base da pirâmide
h → altura da pirâmide
A base de uma pirâmide pode ser formada por qualquer polígono, então, podemos ter uma pirâmide de base triangular, pirâmide de base quadrada, pirâmide de base hexagonal. Enfim, qualquer polígono pode ser base da pirâmide, e, como se trata de um polígono, para calcular a área da sua base, há uma fórmula específica.
Leia também: Quais são os sólidos de Platão?
Pirâmide de base quadrada
Em uma pirâmide de base quadrada, sabemos que a área do quadrado é calculada pelo comprimento do lado ao quadrado, ou seja, A = l². Então, para calcular o volume de uma pirâmide quadrada, calculamos o produto entre o quadrado da aresta da base e a altura da pirâmide, e dividimos por três. Veja um exemplo a seguir.
Exemplo:
Calcule o volume da pirâmide a seguir, sabendo que a sua base é formada por um quadrado:
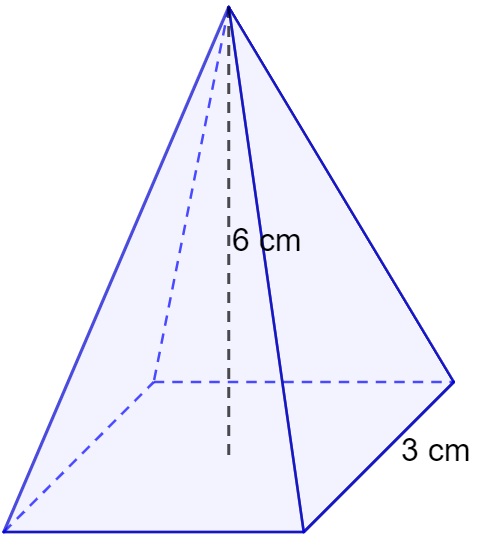
Na pirâmide temos que a altura h mede 6 cm e a aresta da sua base mede 3 cm.
Então, calcularemos, primeiro, a área da base Ab. A área do quadrado é igual a l², então, temos que:
Ab = l²
Ab = 3²
Ab = 9 cm²
Agora que conhecemos o valor da área da base, basta substituir a medida da altura e a medida da área da base na fórmula do volume da pirâmide:
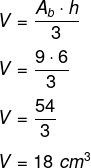
Pirâmide de base triangular
Quando a base da pirâmide é triangular, para calcular a área da base, utilizamos a fórmula da área de um triângulo, que é igual ao produto da base pela altura dividido por dois.
Exemplo:
Sabendo que a pirâmide a seguir tem 9 cm de altura, calcule o seu volume:
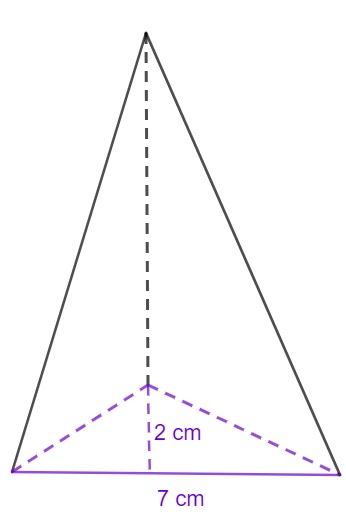
Como a base é um triângulo, primeiro calcularemos a área da base, que é o comprimento da base vezes o comprimento da altura do triângulo que forma a base, dividindo por dois.
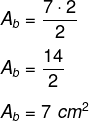
Agora que conhecemos o valor da área da base, torna-se possível calcular o volume dessa pirâmide:
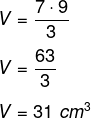
Exemplo 2:
Quando a base da pirâmide for um triângulo equilátero, podemos utilizar a fórmula da área do triângulo equilátero para calcular a área da base.
Calcularemos o volume de uma pirâmide cuja base é um triângulo equilátero de lados medindo 8 cm, e sua altura mede 15 cm.
Primeiro calculamos a área da base, como ela é um triângulo equilátero, utilizaremos a fórmula da área de um triângulo equilátero.
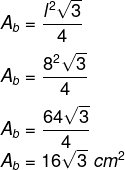
Agora calcularemos o volume:
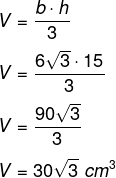
Veja também: Diferenças entre figuras planas e espaciais
Pirâmide de base hexagonal
Na pirâmide de base hexagonal, para calcular a área da base, utilizamos a fórmula da área do hexágono.
Exemplo:
Calcule o volume da pirâmide sabendo que sua base é um hexágono regular:
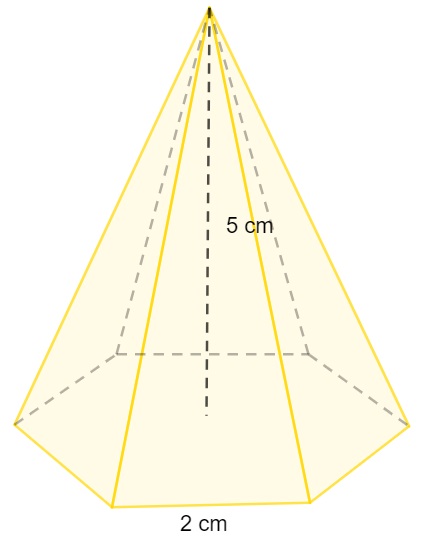
Primeiro calcularemos a área do hexágono:
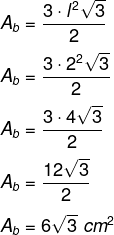
Agora calcularemos o volume:
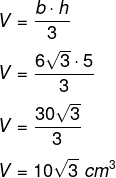
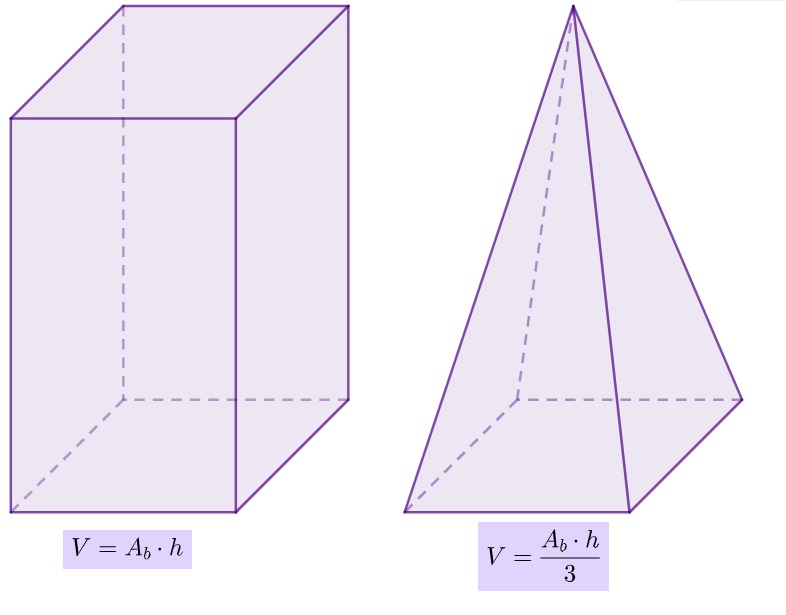
Relação entre volume da pirâmide e volume do prisma
Dado um prisma e uma pirâmide de mesma base, sabemos que o volume do prisma é igual ao produto entre a área da base e a altura, e que o volume da pirâmide é o produto entre a área da base e a altura divido por três, então, se a área da base for a mesma, o volume da pirâmide será igual a 1/3 do volume do prisma.
Exercícios resolvidos
Questão 1 - Buscando inovar no design das embalagens, uma indústria de cosmético decidiu produzir embalagens no formato de uma pirâmide de base quadrada para o seu novo hidratante. A base dessa pirâmide tem o formato de um quadrado de lados medindo 6 cm. Sabendo que esse hidratante deve conter 200 ml, a altura da pirâmide tem de ser, aproximadamente:
A) 15,2 cm
B) 15,8 cm
C) 16,4 cm
D) 16,7 cm
E) 17,2 cm
Resolução
Alternativa D
Sabemos que 200 ml é igual a 200 cm³, logo, temos que V = 200. Então, calculando a área da base, que é um quadrado, temos que:
Ab = l²
Ab = 6²
Ab = 36 cm²
Agora vamos igualar o volume a 200 cm³, então, temos que:
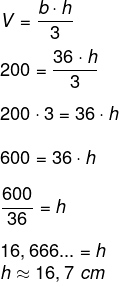
Questão 2 - (Enem) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
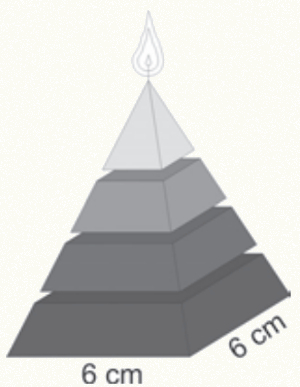
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
A) 156 cm³
B) 189 cm³
C) 192 cm³
D) 216 cm³
E) 540 cm³
Resolução
Alternativa B
Vamos calcular a diferença entre a pirâmide maior (V) e a pirâmide menor (V2).
Sabemos que há 1 cm de distância entre os blocos, então, a altura da pirâmide maior é de 19 – 3 = 16 cm. A pirâmide maior tem 6 cm de lado da base, como a base é um quadrado, então, Ab = l² = 6² = 36.
Dessa forma, o volume da pirâmide maior é:
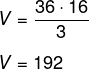
Para encontrar a altura da pirâmide menor, vamos dividir a altura total por 4, então, 16 : 4 = 4 cm. Fazendo o mesmo com a aresta, temos que 6 : 4 = 1,5.
Assim, a área da base da pirâmide menor é 1,5² = 2,25. Calculando o volume, temos que:
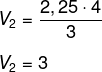
Agora encontramos a diferença entre os volumes:
192 – 3 = 189 cm³
Por Raul Rodrigues de Oliveira
Professor de Matemática




