Quando falamos em dimensões, referimo-nos à possibilidade de mensurar objetos dentro de um espaço. Cada uma das direções em que é possível realizar medidas em um espaço é chamada de dimensão. Se não existe possibilidade de tomar outra medida além do comprimento de um objeto, por exemplo, dizemos que esse objeto possui apenas uma dimensão.
Para compreender a ideia de dimensão, o melhor caminho é observar objetos que pertencem a diferentes dimensões e analisá-los com relação às suas medidas. Observe:
Espaço unidimensional
A reta é um objeto unidimensional, isto é, possui apenas uma dimensão. Observando bem uma reta, é possível notar que qualquer medida feita sobre ela representará apenas um comprimento. Dessa maneira, pode-se afirmar que retas não possuem largura, apenas comprimento. A distância entre dois pontos quaisquer de uma reta pode variar entre zero e infinito, contudo, a largura de uma reta sempre será zero porque ela possui apenas uma dimensão.

Reta: Espaço unidimensionalTítulo: Exemplo de espaço unidimensional
Na realidade, como a reta é um objeto infinito, ela é todo o espaço unidimensional. Os objetos pertencentes a esse espaço são representados por semirretas, segmentos de reta, pontos e conjuntos de pontos.
Espaço bidimensional
O quadrado é um exemplo de figura bidimensional. Isso significa que é possível encontrar tanto largura quanto comprimento de um quadrado (e de qualquer outra figura geométrica bidimensional). Contudo, a profundidade do quadrado não existe, pois ele não é uma figura que possui três dimensões. Dessa maneira, se uma pessoa se atirasse a uma piscina quadrada bidimensional, pararia na superfície da piscina, pois esta não possui profundidade.

Figura da esquerda: vista superior de um quadrado. Figura da direita: vista lateral de um quadrado
A figura acima mostra um quadrado visto de cima. Veja que é possível medir seu comprimento e largura. A vista lateral de um quadrado, por sua vez, resume-se a um segmento de reta.
O espaço que possui duas dimensões é conhecido como plano. Desse modo, toda a geometria plana tem como base o espaço bidimensional.
Espaço tridimensional
A pirâmide é uma figura tridimensional. Qualquer observador atento notaria que as pirâmides do Egito, por exemplo, têm como base um quadrado, que é uma figura bidimensional. Contudo, acima desse quadrado, existe um grande volume de pedras sobrepostas que culminam em um vértice superior. As medidas possíveis para figuras geométricas tridimensionais são: comprimento, largura e profundidade.
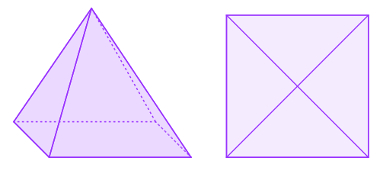
Figura da Direita: Vista frontal de uma pirâmide. Figura da Esquerda: Vista superior de uma pirâmide
Observe na imagem acima que a vista superior de uma pirâmide é exatamente o formato de sua base. Dessa forma, vista por cima, percebe-se apenas uma figura de duas dimensões. É necessário rotacioná-la para perceber sua profundidade. O mesmo ocorre com a vista lateral do quadrado: também é necessário rotacioná-lo para compreender sua segunda dimensão.
Espaços multidimensionais
Qualquer objeto presente em um espaço pode ter nascido em determinada época e findar em algum tempo. A quarta dimensão é a representante do tempo. Um objeto quadridimensional ocupa uma posição no espaço em um certo período de tempo.
As dimensões seguintes não são representadas geometricamente nem percebidas pelos sentidos humanos (não ainda). Contudo, os cálculos matemáticos que as consideram comprovam sua existência e já são utilizados em diversos campos de estudo e pesquisa, como a informática.
Existem objetos que não possuem dimensão alguma?
Objetos que não possuem dimensão são aqueles em que não é possível tomar medida alguma. Por exemplo, a reta possui uma dimensão e nela é possível calcular comprimentos e distâncias entre dois pontos. Já o quadrado possui duas dimensões e nele é possível calcular tanto comprimentos quanto larguras.
Um exemplo de objeto matemático que não possui dimensão é o ponto. Não é possível tomar medida alguma em um ponto. Não há que se falar em comprimento de um ponto, largura de um ponto etc. Na realidade, pontos relacionam-se com localizações no espaço e também são considerados objetos primitivos que dão base à toda geometria moderna.
Por Luiz Paulo Moreira
Graduado em Matemática
