Esfera

A esfera é um sólido geométrico estudado na geometria espacial, sendo classificada como um corpo redondo. Essa forma é bastante comum no dia a dia, como podemos vê-la na bola de futebol, nas pérolas, no globo terrestre, em alguns frutos, entre outros exemplos.

Considerando O a origem e r o raio, a esfera é o conjunto de pontos que estão a uma distância igual ou menor que a distância entre o raio e a origem. Além do raio, a esfera possui elementos importantes, como os polos, o equador, o meridiano e os paralelos. Podemos também dividir a esfera em partes como o cunho e o fuso esférico. A área total e o volume de uma esfera são calculados por fórmulas específicas que dependem apenas do valor do raio dessa figura.

Leia também: Diferenças entre figuras planas e espaciais

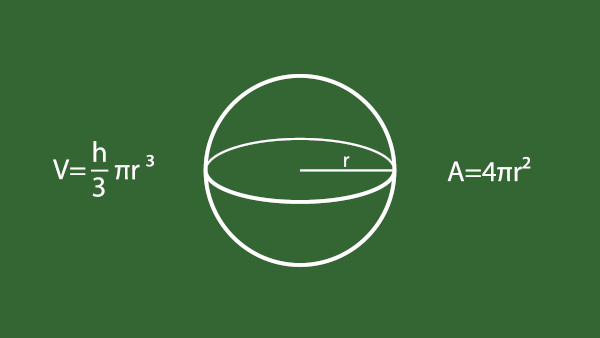
Tópicos deste artigo

• 1 - Elementos de uma esfera
• 2 - Volume da esfera
• 3 - Superfície da esfera
• 4 - Partes da esfera
  • Fuso esférico
  • Cunha esférica 
• 5 - Exercícios resolvidos

Elementos de uma esfera

Conhecemos como esfera todos os pontos no espaço que estão a uma distância igual ou menor que o raio da sua origem, por isso dois elementos importantes dessa figura são o raio r e a origem O. A esfera é classificada como um corpo redondo por conta do formato da sua superfície.

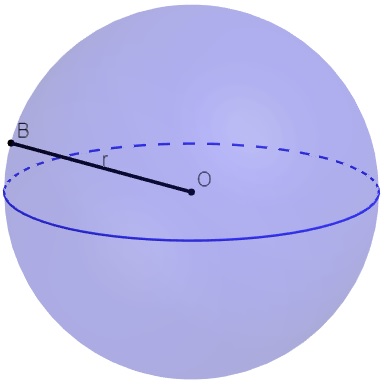
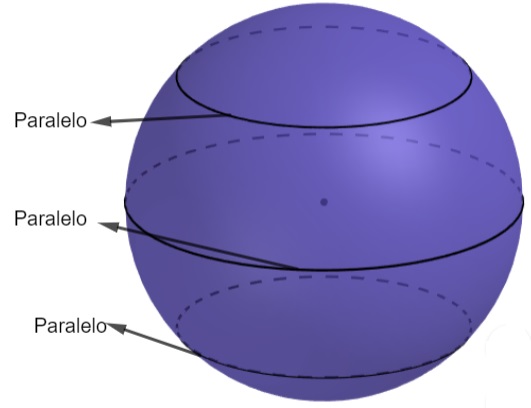
Outros elementos importantes para a esfera são os polos, equador, paralelos e meridiano.

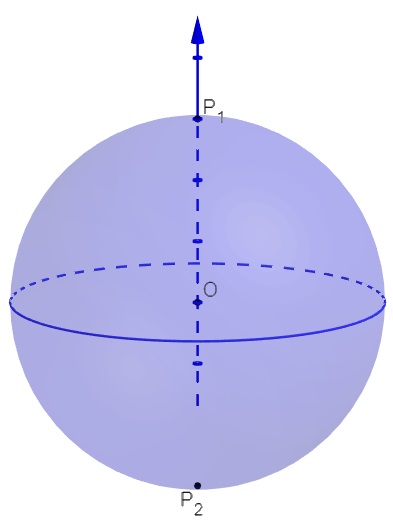
• Polos: representados pelos pontos P₁  e P₂, são os pontos de encontro da esfera com o eixo central.

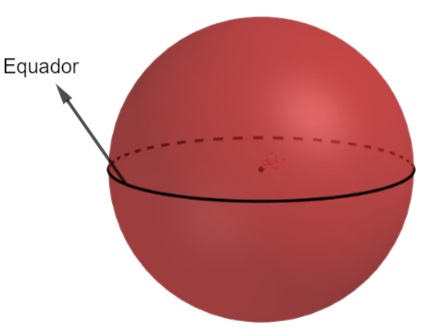
• Equador: a maior circunferência que conseguimos ao interceptar a esfera por um plano na horizontal. O equador divide a esfera em duas partes iguais conhecidas como hemisférios.

• Paralelos: qualquer circunferência que conseguimos ao interceptar a esfera por um plano na horizontal. O equador, que mostramos anteriormente, é um caso particular de paralelos e o maior deles.

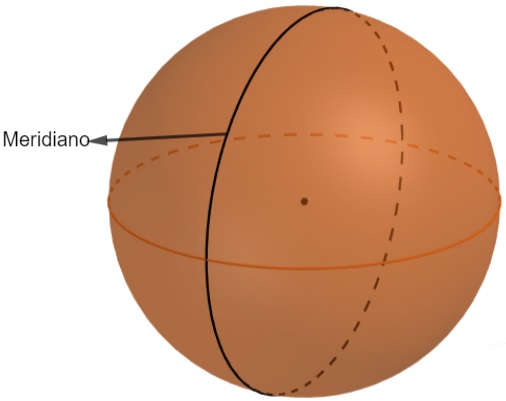
• Meridiano: a diferença entre meridiano e paralelos é que o primeiro é obtido na vertical, mas também é uma circunferência contida na esfera e obtida pela interceptação de um plano.

Saiba mais detalhes dos elementos desse importante sólido geométrico lendo: Elementos de uma esfera.

Volume da esfera

O cálculo do volume de sólidos geométricos é de grande importância para sabermos a capacidade desses sólidos, e com a esfera não é diferente, é de grande importância calcular seu volume para sabermos, por exemplo, a quantidade de gás que podemos colocar em um recipiente esférico, entre outras aplicações. O volume de uma esfera é dado pela fórmula:

Exemplo:

Um reservatório de gás possui um raio igual a 2 metros, sabendo-se disso, qual é o seu volume? (use π = 3,1)

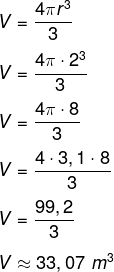
Superfície da esfera

Conhecemos como superfície da esfera a região formada por todos os pontos que estão à distância r da esfera. Note que, neste caso, a distância não pode ser menor, mas sim exatamente igual a r. A superfície da esfera é o contorno de todo o sólido, é a superfície que reveste a esfera. Para calcular a área da superfície da esfera, utilizamos a fórmula:

Exemplo:

Em um hospital, será construído um reservatório de gás oxigênio no formato de uma esfera. Sabendo que ele possui 1,5 metro de raio, qual será a área de sua superfície em m²?

A_t = 4 π r²

A_t = 4 π 1,5²

A_t = 4 π 2,25

A_t = 9 π m²

Veja também: Quais as diferenças entre círculo e circunferência?

Partes da esfera

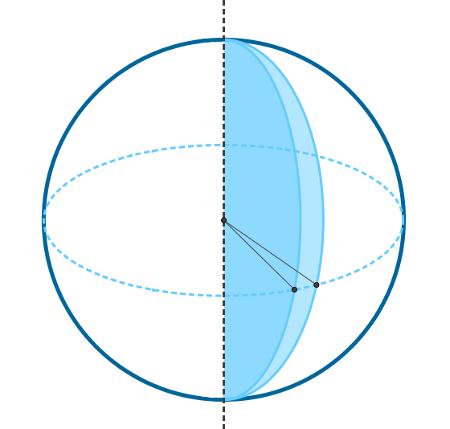
Podemos dividir a esfera em partes, conhecidas como fuso, quando consideramos somente a sua superfície, ou como cunha, quando consideramos o sólido. 

• Fuso esférico

O fuso é a superfície formada pela rotação de uma semicircunferência quando essa rotação (θ) é menor que 360º, ou seja, quando 0 < θ < 360º.

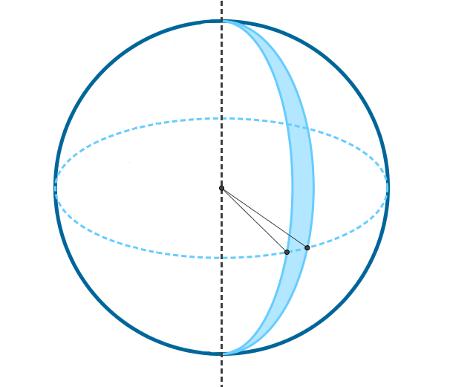
Como o fuso é parte da superfície de uma esfera, calculamos a sua área, que pode ser deduzida por regra de três, gerando a seguinte fórmula:

Exemplo:

Calcule a área do fuso e o volume da cunha sabendo que θ = 30º e r = 3 metros.

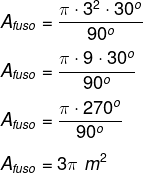
• Cunha esférica 

Chamamos de cunha esférica o sólido geométrico formado pela rotação de um semicírculo, quando essa rotação é menor que 360º, ou seja, 0 < θ < 360º.

Como a cunha é um sólido geométrico, calculamos o seu volume, o que, assim como a área do fuso, pode ser feito por meio de uma regra de três, que gera a fórmula:

Exemplo:

Calcule o volume da cunha sabendo que r = 4 cm e θ = 90º:

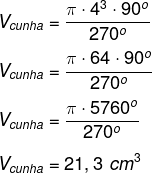
Exercícios resolvidos

Questão 1 - Ao analisar-se um vírus em um microscópio, foi possível perceber que ele possui duas camadas, sendo a primeira camada formada por gordura e a camada central formada por material genético, conforme a imagem a seguir:

Um dos interesses desse pesquisador é saber o volume da camada de gordura desse vírus. Sabendo que o raio maior mede 2 nm (nanômetros) e que o raio menor mede 1 nm, o volume da camada de gordura é igual a:

(use π = 3)

a) 4 nm³

b) 8 nm³

c) 20 nm³

d) 28 nm³

e) 32 nm³

Resolução

Alternativa D.

Calcular o volume da camada azul, ou seja, de gordura, é o mesmo que calcular a diferença entre o volume da esfera maior V_E e o da esfera menor V_e.

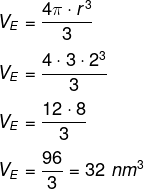
Agora calcularemos o volume da esfera menor:

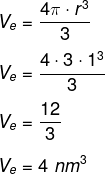
Então a diferença entre os volumes é igual a:

VE – Ve = 32 – 4 = 28 nm³

Questão 2 - Uma fábrica produz porta-objetos, no formato de esfera, utilizando um plástico especial. Sabendo que o cm² desse material custa R$ 0,07, o valor gasto para produzir 1,2 mil porta-objetos, cujo raio é de 5 cm, será:

(use π = 3,14)

a) R$ 2180

b) R$ 3140

c) R$ 11.314

d) R$ 13.188

e) R$ 26.376

Resolução

Alternativa E.

Vamos calcular a área total de uma esfera:

At = 4 π r²

At = 4 · 3,14 · 5²

At =  12,56 · 25

At =  12,56 · 25

At =  314 cm²

Ao multiplicar 314 por 0,07, teremos o valor de um porta-objetos, logo, se multiplicarmos esse valor por 1,2 mil, teremos o valor total gasto.

V = 314 · 0,07 · 1200 = 26.376        

Por Raul Rodrigues de Oliveira
Professor de Matemática