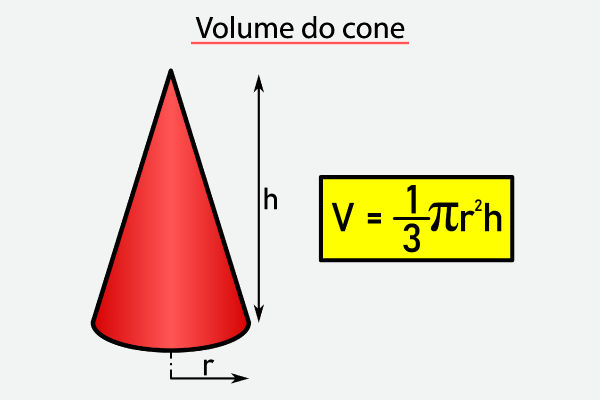
O volume de um cone é dado pela multiplicação da área da base pela altura, dividida por três, ou seja: \(V = \frac{\pi r^2 h}{3}\). Como a base é um círculo, utilizamos a fórmula da área do círculo (\(A_b = \pi r^2\)), em que r é o raio da base do cone. Após encontrar a área da base, basta multiplicá-la pela altura h do cone e dividir por 3. Assim, obtemos o valor do volume desse sólido.
Leia também: Como calcular o volume do cubo
Tópicos deste artigo
- 1 - Resumo sobre o volume do cone
- 2 - Videoaula sobre o volume do cone
- 3 - Fórmula do volume de cone
- 4 - Como calcular o volume do cone
- 5 - Volume do tronco de cone
- 6 - Exercícios sobre volume de cone
Resumo sobre o volume do cone
- O volume do cone é calculado a partir do raio da base do cone e da altura do cone.
- A fórmula do volume do cone é:\(V = \frac{\pi r^2 h}{3}\)
- Além do volume do cone, existe o tronco de cone, que é um sólido geométrico gerado quando um cone é cortado por um plano paralelo a sua base.
- A fórmula do volume do tronco de cone é:
\(V = \frac{1}{3} \pi h \left( R^2 + r^2 + Rr \right) \)
Videoaula sobre o volume do cone
Fórmula do volume de cone
O volume de um cone é calculado pelo produto entre a área da base e a altura dividido por três. Como a base do cone é um círculo (a área do círculo é πr2), então a fórmula do volume do cone é:
\(V = \frac{\pi r^2 h}{3}\)
- V: volume.
- h: altura do cone.
- r: raio da base do cone.
Como calcular o volume do cone
Para descobrir o volume de um cone, é necessário conhecer as medidas do raio da base e da altura. Com esses valores, basta aplicar na fórmula do volume e fazer os cálculos indicados.
Exemplo 1:
Calcule o volume de um cone que possui raio igual a 4 cm e altura de 9 cm.
Resolução:
Dados:
- r = 4 cm
- h = 9 cm
Então o volume será:
\(V = \frac{\pi r^2 h}{3}\\ V = \frac{\pi \cdot 4^2 \cdot 9}{3}\\ V = \frac{16 \cdot 9 \pi}{3}\\ V = \frac{144 \pi}{3}\\ V = 48 \, \text{cm}^3 \)
Exemplo 2
Calcule o volume do cone a seguir:
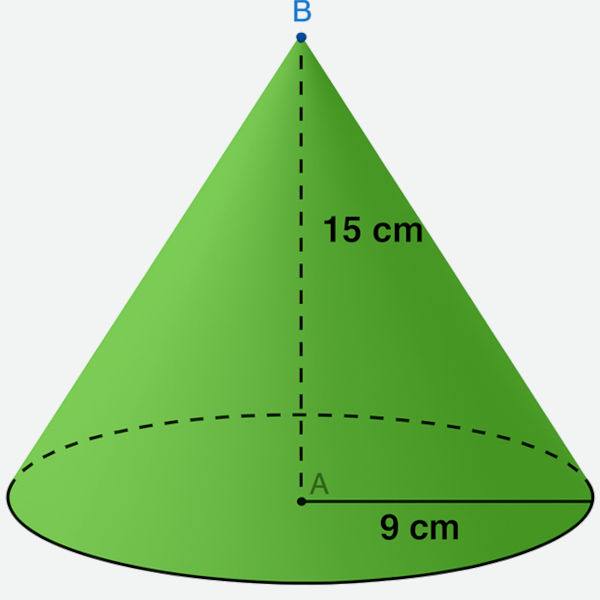
Resolução:
Dados:
- h = 15
- r = 9
Substituindo na fórmula:
\(V = \frac{\pi r^2 h}{3} \\ V = \frac{\pi \cdot 9^2 \cdot 15}{3} \\ V = \frac{\pi \cdot 81 \cdot 15}{3} \\ V = \frac{1215 \pi}{3} \\ V = 405 \pi \, \text{cm}^3 \\ \)
Volume do tronco de cone
O tronco de cone é um sólido geométrico encontrado quando um cone é cortado por um plano paralelo a sua base. O corte resulta em uma figura que tem duas bases circulares: uma maior e uma menor, além de uma altura e uma forma que se assemelha a um cone, mas sem o vértice.
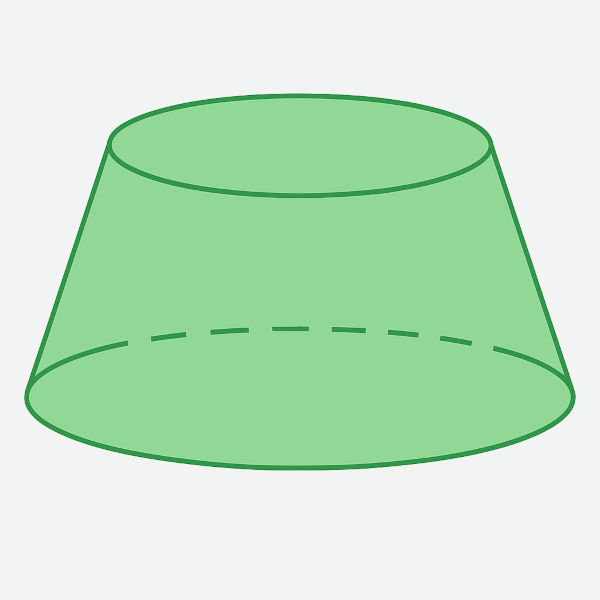
Para calcular o volume do tronco do cone, utilizamos a fórmula:
\(V = \frac{1}{3} \pi h \left( R^2 + r^2 + Rr \right) \\ \)
- R: raio da base maior
- r: raio da base menor
- h: altura do tronco de cone
Exemplo:
Um tronco de cone possui raio maior medindo 6 cm, raio menor medindo 3 cm e altura de 10 cm. Qual é o volume desse tronco de cone?
Resolução:
Temos que:
- R = 6
r = 3
h = 10
Substituindo na fórmula:
\(V = \frac{1}{3} \pi r \left( R^2 + r^2 + Rr \right) \\ V = \frac{1}{3} \pi \cdot 3 \left( 6^2 + 3^2 + 6 \cdot 3 \right) \\ V = \frac{1}{3} \pi \cdot 3 \left( 36 + 9 + 18 \right) \\ V = \frac{1}{3} \pi \cdot 3 \cdot 63 \\ V = 63 \pi \, \text{cm}^3 \\\)
Exercícios sobre volume de cone
Questão 1
(Enem 2010) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.
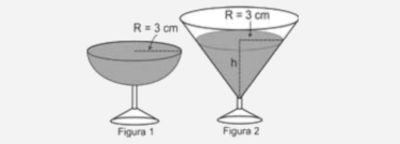
Considere:
\(V_{\text{esfera}} = \frac{4}{3} \pi R^3 \\ \) e \(V_{\text{cone}} = \frac{1}{3} \pi R^2 h \\ \)
Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de:
A) 1,33
B) 6,00
C) 12,00
D) 56,52
E) 113,04
Resolução:
Alternativa B
O hemisfério é metade de uma esfera, logo temos que:
\(V_h = \frac{\frac{4}{3} \pi R^3}{2} \\ V_h = \frac{4}{6} \pi R^3 \\ V_h = \frac{4}{6} \pi \cdot 3^3 \\ V_h = \frac{4}{6} \pi \cdot 27 \\ V_h = 18 \pi \, \text{cm}^3\)
Agora o volume do cone:
\(V = \frac{1}{3} \pi r^2 h \\ V = \frac{1}{3} \pi 3^2 h \\ V = 3 \pi h\)
Sabemos que o volume é igual, então temos que:
\(3 \pi h = 18 \pi \\ h = \frac{18 \pi}{3 \pi} \\ h = 6\)
Questão 2
Um cone tem raio da base igual a 6 cm e altura igual a 12 cm. Qual é o volume desse cone? (Use π= 3,14)
A) 226,08 cm3
B) 301,44 cm3
C) 452,16 cm3
D) 678,24 cm3
E) 904,32 cm3
Resolução:
Alternativa C
Calculando o volume, temos que:
\(V = \frac{1}{3} \pi r^2 h \\ V = \frac{1}{3} \cdot 3,14 \cdot 6^2 \cdot 12 \\ V = \frac{1}{3} \cdot 3,14 \cdot 36 \cdot 12 \\ V = \frac{1}{3} \cdot 3,14 \cdot 432 \\ V = \frac{1}{3} \cdot 1356,16 \\ V = 452,16\)
Fontes
DANTE, L. R. Matemática: contexto & aplicações – Ensino Médio. 3. ed. São Paulo: Ática, 2016. v.3.
DOLCE, O; POMPEO, J. N. Fundamentos de matemática elementar, Vol 10: Geometria espacial - Posição e métrica. 7 ed. Santos: Atual, 2013.