Volume do tronco de cone

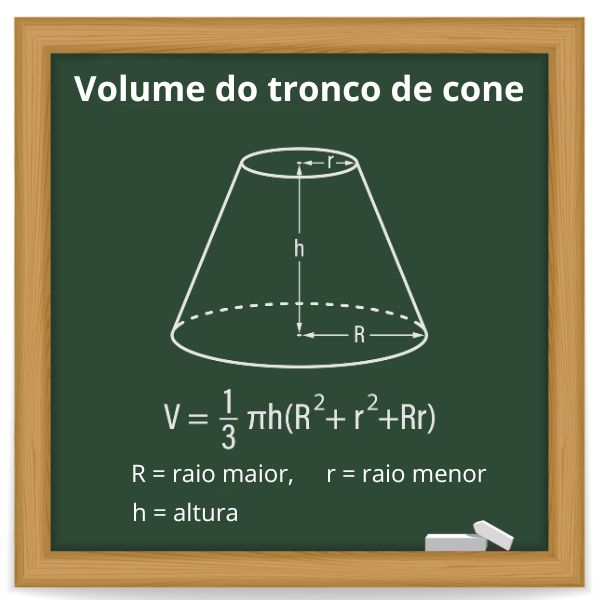
O volume do tronco de cone é o espaço ocupado por esse corpo redondo. Como a secção transversal de um cone de raio R produz um cone menor de raio r e um tronco de cone, os volumes desses três sólidos estão relacionados.

Leia também: Como calcular o tronco de uma pirâmide

Tópicos deste artigo

• 1 - Resumo sobre o volume do tronco de cone
• 2 - Videoaula sobre o volume do tronco de cone
• 3 - Quais são os elementos do tronco de cone?
• 4 - Fórmula do volume do tronco de cone
• 5 - Como calcular o volume do tronco de cone?
• 6 - Exercícios resolvidos sobre o volume do tronco de cone

Resumo sobre o volume do tronco de cone

• Um cone de raio R seccionado transversalmente a uma altura h do plano da base é dividido em dois sólidos geométricos: um cone de raio r e um tronco de cone.
• Os principais elementos do tronco de cone são a altura h, a base menor de raio r e base maior de raio R.
• O volume do tronco de cone é a diferença entre o volume do cone de raio R e o volume do cone de raio r.
• A fórmula do volume do tronco de cone é:

\(V_t=\frac{1}{3} πh(R^2+r^2+Rr)\)

Videoaula sobre o volume do tronco de cone

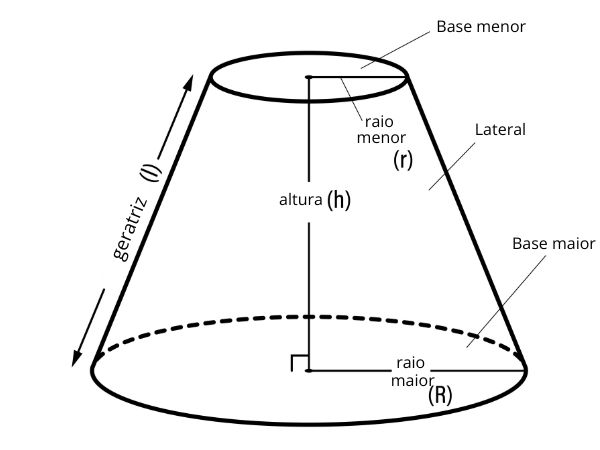
Quais são os elementos do tronco de cone?

Os elementos de um tronco de cone formado da secção de um cone reto de raio R  são:

• Base menor – círculo de raio r, obtido na secção do cone de raio R .
• Base maior – base circular do cone de raio R .
• Altura (h) – distância entre os planos das bases.
• Geratriz – segmento com extremidades nas circunferências que delimitam as bases.

A imagem abaixo apresenta os elementos de um tronco de cone. Note que as bases menor e maior são paralelas.

Fórmula do volume do tronco de cone

A seguir, vamos deduzir a fórmula do volume de um tronco de cone de altura h, raio da base menor r e raio da base maior R .

Considere que a secção transversal de um cone de raio R  e altura H₁ produz dois sólidos:

• um cone de raio r e altura H₂ e
• um tronco de cone de altura h .

Perceba que \(H_1=H_2+h\).

O volume do cone de raio R (que chamaremos de cone maior) será representado por VR; o volume do cone de raio r (que chamaremos de cone menor), por Vr ; e o volume do tronco de cone, por Vt. Portanto:

\(V_R=V_r+V_t\)

Note que:

• \( V_R=\frac{1}{3} πR^2 H_1=\frac{1}{3} πR^2 (H_2+h)\)
• \( V_r=\frac{1}{3}1/3 πr^2 H_2\)

Observação: VR  e Vr  são volumes de cones. Para revisar este assunto, clique aqui.

Assim:

\(V_R=V_r+V_t\)

\(\frac{1}{3} πR^2 (H_2+h)=1/3 πr^2 H_2+V_t\)

\(V_t=\frac{1}{3} πR^2 (H_2+h)-1/3 πr^2 H_2\)

\(V_t=\frac{1}{3} πR^2 H¬_2+1/3 πR^2 h-1/3 πr^2 H_2\)

\(V_t=\frac{1}{3} π(R^2 H_2+R^2 h-r^2 H_2 )\)

\(V_t=\frac{1}{3} π[R^2 h+(R^2-r^2 ) H_2 ]\)

O termo H2  corresponde à altura do cone menor. Relacionando as alturas dos cones com os respectivos raios das bases, podemos obter uma fórmula para o volume do tronco que dependa apenas dos elementos do tronco (R, r e h).

Associando o raio e a altura do cone maior (R e H₁ ) com o raio e a altura do cone menor (r e H₂), temos a seguinte proporção:

\(\frac{R}{H_1}=\frac{r}{H_2}\)

\(\frac{R}{H_2+h}=\frac{r}{H_2}\)

\(RH_2=rH_2+rh\)

\(H_2=\frac{rh}{R-r}\)

Logo, podemos reescrever o volume do tronco Vt  do seguinte modo:

\(V_t=\frac{1}{3} π[R^2 h+(R^2-r^2 ) H_2 ]\)

\(V_t=\frac{1}{3} πh[R^2h+(R^2-r^2 ) \frac{rh}{R-r}]\)

\(V_t=\frac{1}{3} πh[R^2+(R^2-r^2 ) \frac{r}{R-r}]\)

\(V_t=\frac{1}{3} πh[R^2+(R+r)(R-r) \frac{r}{R-r}]\)

\(V_t=\frac{1}{3} πh[R^2+(R+r)r]\)

Assim, a fórmula do volume do tronco de cone é:

\(V_t=\frac{1}{3}πh(R^2+r^2+Rr)\)

Leia também: Fórmulas de volumes de diversos sólidos geométricos

Como calcular o volume do tronco de cone?

Para calcular o volume de um tronco de cone, basta substituir na fórmula as medidas da altura, do raio da base menor e do raio da base maior.

• Exemplo: Qual o volume, em centímetros cúbicos, de um tronco de cone em que o raio da base maior é R = 5 cm, o raio da base menor é r = 3  e a altura é h = 2  cm? (Utilize π=3 )

Substituindo os dados na fórmula, temos que:

\(V_t=\frac{1}{3}⋅3⋅2⋅(5^2+3^2+5⋅3)\)

\(V_t=2⋅(49)\)

\(V_t=98 cm³\)

Exercícios resolvidos sobre o volume do tronco de cone

Questão 1

Um pote tem o formato de um tronco de cone com raio da base maior R = 8  cm, raio da base menor r = 4  e a altura h = 2 cm. O volume desse pote, em cm³, é:

a) 48 π

b) 64 π  

c)112 π

d)448 π  

e) 1344 π

Resolução

Substituindo os dados na fórmula, temos que:

\(V_t=\frac{1}{3}⋅π⋅12⋅(8^2+4^2+8⋅4)\)

\(V_t=4π⋅(112)\)

\(V_t=448 π\)

Alternativa D

Questão 2

(Enem 2021) Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

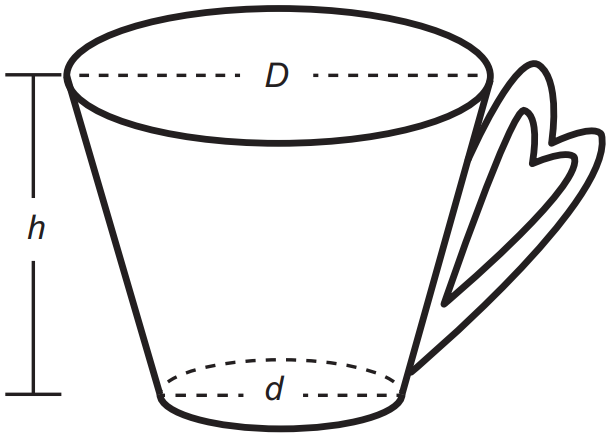
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm.

Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).

Utilize 3 como aproximação para π.

Qual é a capacidade volumétrica, em mililitro, dessa caneca?

a) 216

b) 408

c) 732

d) 2196

e) 2928

Resolução

O formato da caneca é um tronco de cone em que o topo é a base maior. Além disso, R=5 , r = 4  cm e h = 12 . Logo:

\(V_t=\frac{1}{3} πh(R^2+r^2+Rr)\)

\(V_t=\frac{1}{3}⋅3⋅12⋅(5^2+4^2+5⋅4)\)

\(V_t=12⋅(61)\)

\(V_t=732 cm³\)

Como 1 cm³ = 1 mL, temos que 732 cm³ = 732 mL.

Alternativa C

Fontes:

DANTE, L. R. Matemática: contexto & aplicações – Ensino Médio. 3. ed. São Paulo: Ática, 2016. v.3.

DOLCE, O; POMPEO, J. N. Fundamentos de matemática elementar, Vol 10: Geometria espacial - Posição e métrica. 7 ed. Santos: Atual, 2013.