Circunferência

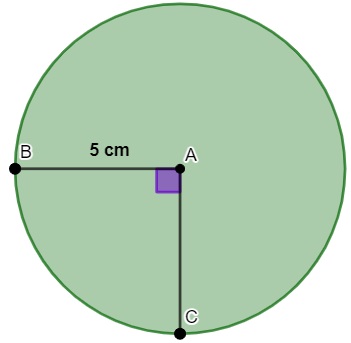
A circunferência é uma figura geométrica plana formada pela união de pontos equidistantes, ou seja, possuem a mesma distância de um ponto fixo chamado de centro. O estudo da circunferência também está presente na geometria analítica, na qual é possível deduzir uma equação que a represente.

Embora o círculo e a circunferência sejam figuras geométricas planas com alguns elementos em comum, o que geralmente acarreta dúvidas, essas figuras apresentam diferenças importantes sobretudo no que diz respeito à dimensionalidade.

Leia também: Distância entre dois pontos – importante conceito da geometria analítica

Tópicos deste artigo

• 1 - Elementos da circunferência
• 2 - Comprimento da circunferência
• 3 - Área da circunferência
• 4 - Equação reduzida da circunferência
• 5 - Equação geral da circunferência
• 6 - Diferenças entre circunferência e círculo
• 7 - Exercícios resolvidos

Elementos da circunferência

Observe a circunferência:

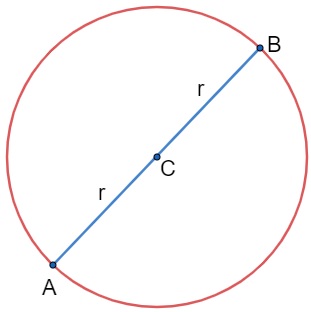
O ponto C é chamado de centro da circunferência, e observe que os pontos A e B pertencem a ela. O segmento que une os extremos da circunferência passando pelo centro é chamado de diâmetro. Na circunferência anterior, temos então que o diâmetro é o segmento AB.

Ao dividir o diâmetro ao meio, vamos obter o raio da circunferência, ou seja, o raio (r) de uma circunferência é o segmento que une o centro e a extremidade. Nesse caso, o raio é o segmento CB. Podemos estabelecer uma relação matemática entre esses dois elementos, uma vez que o diâmetro é o dobro do raio.

d = 2 · r

• Exemplo

Determine o raio de uma circunferência que possui diâmetro medindo 40 cm.

Sabemos que o diâmetro é o dobro do raio, assim:

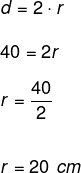
Comprimento da circunferência

Considere uma circunferência que possui raio medindo r. O comprimento ou perímetro da circunferência é dado pelo produto da constante pi (π) pelo dobro do raio.

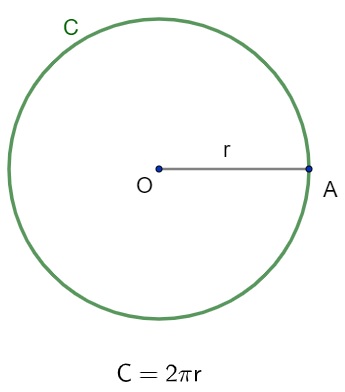
Ao calcularmos o comprimento ou perímetro de uma circunferência, estamos determinando o tamanho da linha verde no desenho anterior, e, para isso, basta substituir o valor do raio na fórmula que procede a figura.

• Exemplo

Determine o comprimento da circunferência de raio 5 cm.

O raio da circunferência é igual 5 cm, logo, para determinar o comprimento da circunferência, devemos substituir esse valor na fórmula.

C = 2πr

C = 2(3,14)(5)

C = 6,24 · 5

C = 31,2 cm

Veja também: Construção de polígonos inscritos

Área da circunferência

Considere uma circunferência de raio r. Para calcular sua área, devemos multiplicar o quadrado do valor do raio por π.

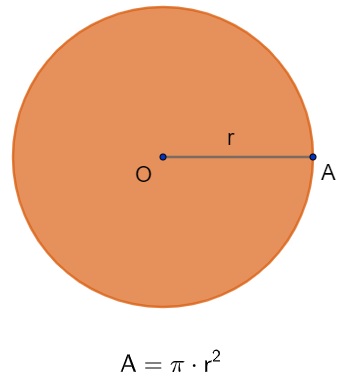
Quando calculamos a área da circunferência, estamos determinando a medida da superfície, ou seja, toda região no interior da circunferência.

• Exemplo

Determine a área de uma circunferência que possui raio igual 4 cm.

Temos que o raio da circunferência é igual a 4 cm, logo, podemos substituir essa medida na fórmula da área. Veja:

A = π · r²

A = 3,14 · (4)²

A = 3,14 · 16

A = 50,24 cm²

Equação reduzida da circunferência

Sabemos que uma circunferência pode ser construída pela coleção de pontos que possuem a mesma distância de um ponto fixo chamado de origem ou centro. Assim, considere um ponto fixo no plano cartesiano O(a, b). O conjunto de pontos — representado por P(x, y) — que estão à mesma distância r desse ponto fixo formará uma circunferência de raio r.

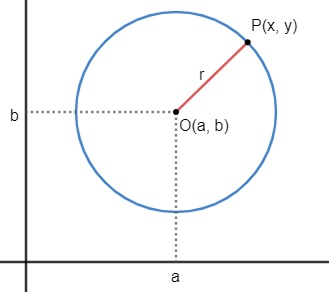
Note que os pontos da forma P(x, y) estão todos à mesma distância do ponto O(a, b), isto é, a distância entre os pontos O e P é igual ao raio da circunferência, assim:

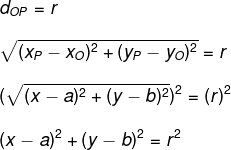
Na equação reduzida, note que os números a e b são as coordenadas do centro da circunferência e que r é a medida do raio.

• Exemplo

Determine as coordenadas do centro e a medida do raio da circunferência que possui equação:

a) (x – 2)² + (y – 6)² = 36

Comparando essa equação com a equação reduzida, temos:

(x – a)² + (y – b)² = r²

(x – 2)² + (y – 6)² = 36

Veja que a = 2, b = 6 e r² = 36. A única equação a resolver-se é:

r² = 36

r = 6

Portanto, a coordenada do centro é: O(2, 6) e o comprimento do raio é 6.

b) (x – 5)² + (y + 3)² = 121

De maneira semelhante, temos:

(x – a)² + (y – b)² = r²

(x – 5)² + (y + 3)² = 121

a = 5

– b = 3

b = –3

Enquanto o valor do raio é dado por:

r² = 121

r = 11

c) x² + y² = 1

(x – a)² + (y – b)² = r²

x² + y² = 1

Observe que x² = (x + 0)² e y² = (y + 0)² . Assim temos que:

(x – a)² + (y – b)² = r²

(x + 0)² + (y + 0)² = 1

Portanto, a coordenada do centro é O(0, 0) e o raio é igual 1.

Acesse também: Como encontrar o centro de uma circunferência?

Equação geral da circunferência

Para determinar a equação geral da circunferência, devemos desenvolver a equação reduzida dela. Assim, considere uma circunferência que possui centro nas coordenadas O(a, b) e raio r.

Inicialmente, desenvolveremos os termos elevados ao quadrado utilizando-nos dos produtos notáveis; em seguida, passaremos todos os números para o primeiro membro; e, por fim, juntaremos os termos com coeficiente literal igual, isto é, os que possuem letras iguais. Veja:

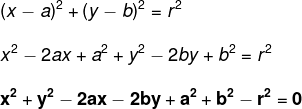
• Exemplo

Determine as coordenas do centro e a media do raio da circunferência que possui equação:

a) x² + y² – 4x – 6y + 4 + 9 – 49 = 0

Para determinar o raio e as coordenadas da circunferência que possui essa equação, devemos compará-la com a equação geral. Veja:

x² + y² – 2ax – 2by + a² + b² – r² = 0

x² + y² – 4x – 6y + 4 + 9 – 49 = 0

Das comparações em verde, temos que:

2a = 4

a = 2

ou

a² = 4

a = 2

Das comparações em vermelho, temos que:

2b = 6

b = 3

ou

b² = 9

b =3

Assim, podemos afirmar que o centro possui coordenada O(2 , 3). Agora, comparando o valor de r, temos:

r² = 49

r = 7

Portanto, o raio da circunferência tem comprimento igual a 7.

b) x² + y² – 10x + 14y + 10 = 0

De maneira semelhante, vamos comparar as equações:

x² + y² – 2ax – 2by + a² + b² – r² = 0

x² + y² – 10x + 14y + 10 = 0

2a = 10

a = 5

Determinando o valor de b:

–2b = 14

b = – 7

Observe agora que:

a² + b² – r² = 10

Como sabemos os valores de a e b, podemos substituí-los na fórmula. Veja:

a² + b² – r² = 10

5² + (–7)² – r² = 10

25 + 49 – r² = 10

74 – r² = 10

– r² = 10 – 74

(–1) – r² = –64 (–1)

r² = 64

r = 8

Portanto, as coordenadas do centro são O (5, –7) e o raio tem comprimento igual a 8.

Diferenças entre circunferência e círculo

A diferença entre uma circunferência e um círculo diz respeito ao número de dimensões de cada elemento. Enquanto a circunferência possui uma dimensão, o círculo possui duas.

A circunferência é uma região no plano formada por pontos todos equidistantes de um ponto fixo chamado de origem. O círculo é constituído por toda região no interior da circunferência. Veja em imagens a diferença:

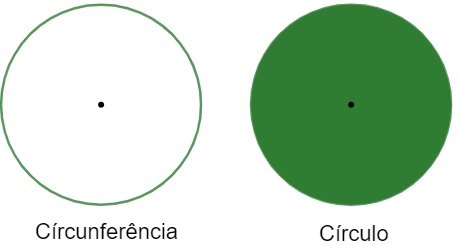
Veja também: Comprimento da circunferência e área do círculo

Exercícios resolvidos

Questão 1 – Uma circunferência possui perímetro igual a 628 cm. Determine o diâmetro dessa circunferência (adote π = 3,14).

Resolução

Como o perímetro é igual a 628 cm, podemos substituir esse valor na expressão de comprimento da circunferência.

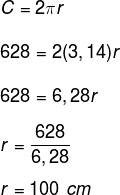
Questão 2 – Duas circunferências são concêntricas se elas possuem o mesmo centro. Sabendo disso, determine a área da figura em branco.

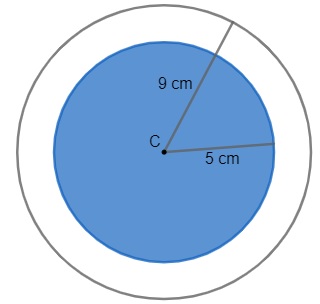
Resolução

Veja que, para determinar a área da região em branco, devemos determinar a área do círculo maior e, em seguida, a do círculo menor em azul. Veja também que se retirarmos o círculo azul sobra somente a região que desejamos, portanto, devemos subtrair essas áreas. Veja:

A_MAIOR = π r²

A_MAIOR = (3,14) · (9)²

A_MAIOR = (3,14) · 81

A_MAIOR = 254,34 cm²

Vamos calcular agora a área do círculo em azul:

A_MENOR = π r²

A_MENOR = (3,14) · (5)²

A_MENOR = (3,14) · 25

A_MENOR = 78,5 cm²

Assim, a área em branco é dada pela diferença entre a área maior e a área menor.

A_BRANCO = 254,34 – 78,5

A_BRANCO = 175,84 cm²

Por Robson Luiz
Professor de Matemática