Prisma

O prisma é um sólido geométrico estudado na geometria espacial. Ele possui duas bases paralelas e formadas por polígonos, e as suas faces laterais são sempre paralelogramos. O prisma recebe um nome de acordo com o formato da sua base. Se a base for um pentágono, por exemplo, ele será um prisma de base pentagonal.

Existem duas classificações possíveis para o prisma, que é o prisma reto, quando ele possui arestas laterais perpendiculares à base, e o prisma oblíquo, quando a aresta lateral não é perpendicular à base. Para calcular a área total e o volume de um prisma, utilizamos fórmulas específicas.

Leia também: Quais são as diferenças entre figuras planas e figuras espaciais?

Tópicos deste artigo

• 1 - Elementos do prisma
• 2 - Bases do prisma
• 3 - Classificação do prisma
• 4 - Área total do prisma
• 5 - Volume do prisma
• 6 - Exercícios resolvidos

Elementos do prisma

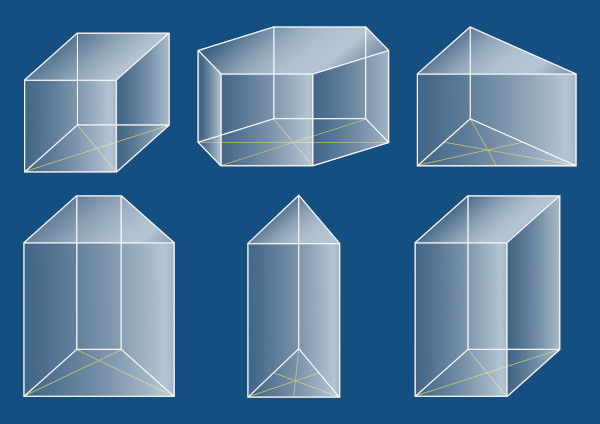
Na geometria espacial, os sólidos geométricos são classificados como poliedros quando possuem todas as suas faces formadas por polígonos. O prisma, que é um caso particular de poliedro, possui duas bases paralelas, com formato de um polígono qualquer, e faces laterais formadas por paralelogramos. Os principais elementos de um prisma são, assim como os outros poliedros:

• as faces,
• os vértices e
• as arestas.

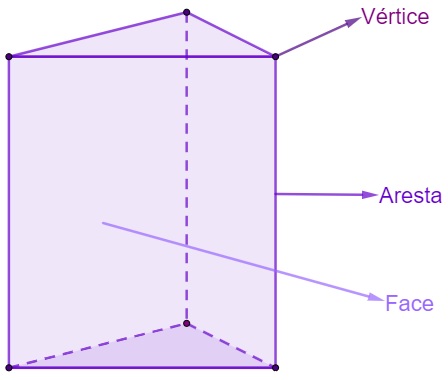
Em um prisma, as faces são os polígonos que formam o sólido geométrico. As arestas são os segmentos de reta formados pelo encontro de duas faces, e os vértices são os pontos.

Bases do prisma

Em um prisma, identificar a sua base é de grande importância, pois é a por meio que conseguimos diferenciar um prisma do outro. Se a base do prisma é triangular, por exemplo, ele é conhecido como prisma de base triangular; se é pentagonal, prisma de base pentagonal, e assim sucessivamente. É por intermédio do polígono que forma a base do prisma, portanto, que podemos diferenciá-lo.

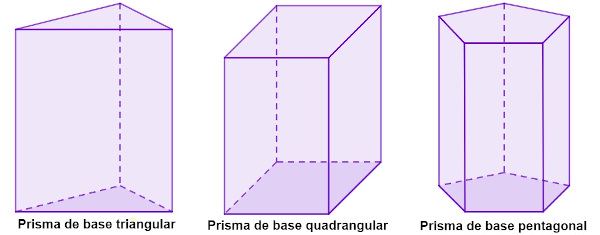
De acordo com a base, o prisma pode ser nomeado como:

• prisma triangular: possui cada uma das bases no formato de um triângulo;
• prisma quadrangular: possui cada uma das bases no formato de um quadrilátero;
• prisma pentagonal: possui cada uma das bases no formato de um pentágono;
• prisma hexagonal: possui cada uma das bases no formato de um hexágono;
• prisma octogonal: possui cada uma das bases no formato de um octógono.

Leia também: Quais são os sólidos de Platão?

Classificação do prisma

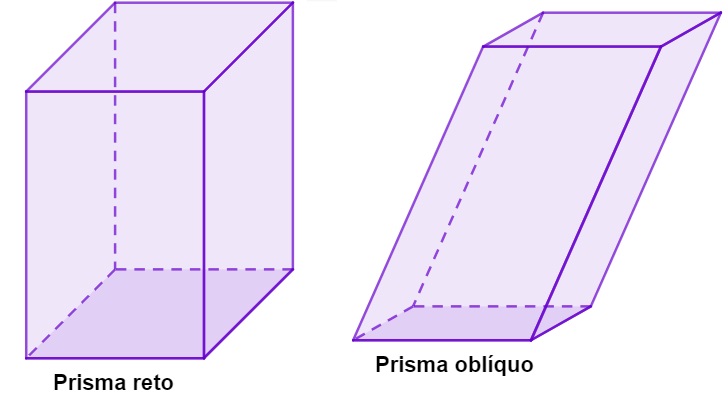
Existem duas classificações possíveis para um prisma: ele pode ser reto, quando as faces laterais formam um ângulo reto com as bases, e pode ser oblíquo, caso a base não faça um ângulo reto com a base.

Área total do prisma

A área total de um poliedro nada mais é do que a soma da área de todas as faces do prisma. Em um prisma, para encontrar a área total, é importante levar em consideração qual é o formato da sua base.

Seja A_b a área da base de um prisma. Sabemos que ele possui duas bases e as áreas laterais, que são sempre paralelogramos. Então, seja S_l  = A_l1 + A_{l2 …} A_ln a soma das áreas laterais. A área total de um prisma qualquer é calculada por:

A_T = 2A_b + S_l

Volume do prisma

Para encontrar o volume do prisma, existe uma fórmula que também depende do formato da base do prisma. O volume de um prisma qualquer pode ser calculado por:

V = A_b · h

Exemplo:

O prisma abaixo possui base quadrangular. Sabendo que a sua base é um quadrado de lados que medem 3 centímetros e  que a altura apresenta 8 centímetros, então, qual é a área total e o volume desse prisma?

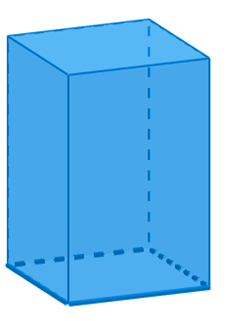
Sabemos que a área do quadrado é igual ao lado ao quadrado, logo:

A_b = l²

A_b = 3²

A_b = 9 cm²

As áreas laterais são todas congruentes e possuem formato de um retângulo de lados com 3 cm e 8 cm. Além disso, é possível perceber que há 4 retângulos que formam a área lateral desse prisma, assim:

A_l = b · h

A_l = 3 · 8

A_l = 24 cm²

Como há 4 retângulos congruentes na área lateral, então:

S_l = 4 · 24 = 96 cm²

A área total desse prisma é calculada por:

AT = 2Ab + Sl

AT = 2·9 + 96

AT = 18 + 96

AT = 114 cm²

Agora calcularemos o volume:

V = A_b · h

V = 9 · 8

V = 72 cm³

Veja também: O que são as formas geométricas?

Exercícios resolvidos

Questão 1 - (FEI) De uma viga de madeira de seção quadrada de lado l = 10 cm extrai-se uma cunha de altura h = 15 cm, conforme a figura. O volume da cunha é:

 

 

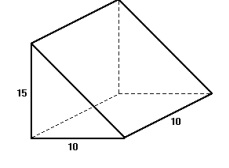
A) 250 cm³

B) 500 cm³

C) 750 cm³

D) 1000 cm³

E) 1250 cm³

Resolução

Alternativa C.

Como a base é um triângulo, sabemos que:

A_b =( b · h) : 2

A_b = (10·15 ): 2

A_b = 150 : 2

A_b = 75 cm²

Agora calcularemos o volume:

V = A_b · h

V = 75 · 10

V = 750 cm³

Questão 2 - Sobre os prismas, julgue as afirmativas a seguir.

I – O cilindro é um prisma que possui bases circulares.

II – Todo poliedro é um prisma, pois ambos possuem faces formadas por polígonos.

III – Um prisma de base triangular possui 6 vértices, 5 faces e 9 arestas.

Estão corretas:

A) somente a afirmativa I.

B) somente a afirmativa II.

C) somente a afirmativa III.

D) somente a afirmativa I e III.

E) Todas as afirmativas estão corretas.

Resolução

Alternativa C.

I → Falsa, pois o cilindro possui base circular, e o círculo não é um polígono, portanto o cilindro não é um prisma.

II → Falsa, pois todo prisma é um poliedro, mas existem poliedros que não são prismas.

III → Verdadeira.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática