Os conceitos de semirreta, semiplano e semiespaço estão intimamente ligados com os conceitos de reta, plano e espaço e podem ser bastante úteis na Geometria para explicar alguns casos e propriedades especiais. Observe esses conceitos e algumas de suas propriedades mais importantes.
Semirreta
Uma reta é um conjunto de pontos infinito, ilimitado, que não faz curva alguma e que não possui “buracos”. Uma semirreta é uma porção de uma reta que tem início em um ponto qualquer e segue para uma de suas direções. Podemos dizer que um ponto divide uma reta em duas semirretas. A figura a seguir mostra essa divisão realizada por um ponto.
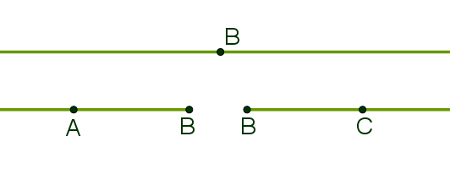
As semirretas acima são representadas pela letra S maiúscula e um índice, formado pelo ponto inicial da semirreta e pelo ponto a que ela se direciona. Portanto, temos as semirretas SBA e SBC. Observe que o ponto A pertence a toda a reta, mas não pertence à semirreta SBC. O ponto C pertence a toda a reta, mas não está na semirreta SBA.
Semiplano
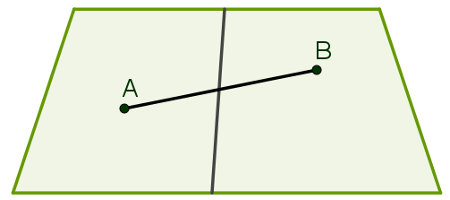
Os planos são superfícies infinitas e ilimitadas e também não fazem curva. Os semiplanos são obtidos quando uma reta divide um plano em duas partes. Isso significa que o plano terá início, mas não terá fim. Uma de suas propriedades é a seguinte: se dois pontos A e B estão em um mesmo semiplano, todos os pontos do segmento de reta AB também estão nesse semiplano.
Da mesma forma, se dois pontos A e B estão em semiplanos distintos, a reta que contém A e B é concorrente à reta que dividiu o plano.
A figura a seguir mostra uma parte de um plano que foi dividido em dois semiplanos e a propriedade discutida acima.
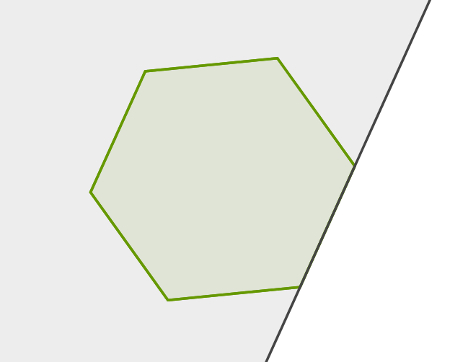
Os semiplanos podem ser usados para definir polígonos convexos. Para tanto, basta que todo o polígono esteja no mesmo semiplano formado por cada um de seus lados. Veja um exemplo de polígono convexo.
Semiespaço
O espaço é o conjunto de todos os planos. É infinito e ilimitado para todas as direções e contém todas as figuras e formas geométricas. É formado por tudo que nos cerca.
Quando uma reta divide o espaço em duas partes, essas partes são chamadas de semiespaços. Imagine que uma caixa de sapatos seja uma pequena parcela do espaço. Se essa caixa for dividida ao meio por um plano, as duas metades representarão os semiespaços. Um esquema dessa comparação pode ser visualizado na figura a seguir:
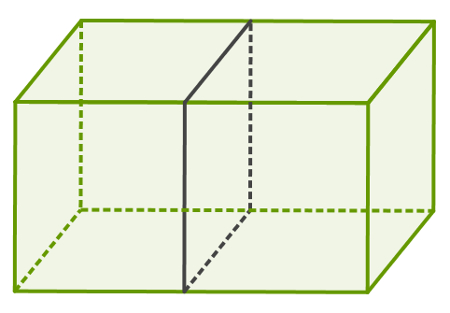
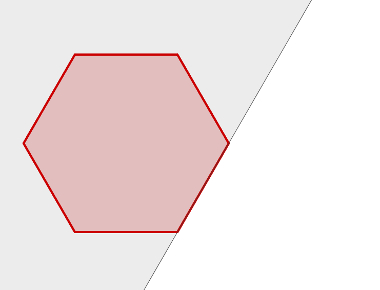
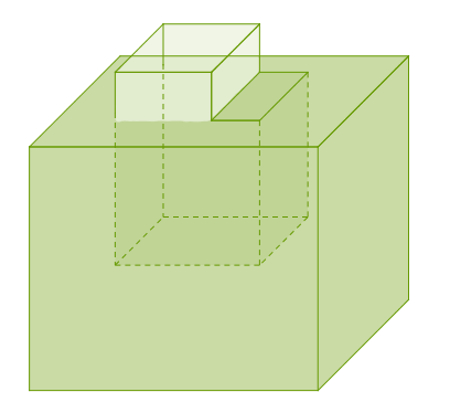
Os semiespaços podem ser usados para determinar poliedros convexos. Se cada face de um poliedro está em um plano que determina dois semiespaços e todo o poliedro está contido em um desses semiespaços, esse poliedro é convexo. Veja um exemplo de poliedro não convexo, pois uma de suas faces determina semiplanos distintos em que ambos contêm pontos do poliedro.
Por Luiz Paulo Moreira
Graduado em Matemática