O volume do prisma é resultado do produto entre a área da base do prisma e a altura. O prisma é um sólido geométrico que tem a duas bases formadas por polígonos congruentes entre si, e as faces laterais são paralelogramos. Como a base do prisma pode ser qualquer polígono, existem diferentes prismas, são eles: prisma de base triangular, prisma de base quadrangular, prisma de base pentagonal, prisma de base hexagonal. O princípio de Cavalieri permite realizar comparações entre volumes de sólidos geométricos que têm mesma altura e secções transversais equivalentes.
Leia também: Como calcular a área do prisma
Tópicos deste artigo
- 1 - Resumo sobre volume do prisma
- 2 - Videoaula sobre volume do prisma
- 3 - Fórmula do volume do prisma
- 4 - Como calcular o volume do prisma?
- 5 - O que é um prisma?
- 6 - Princípio de Cavalieri
- 7 - Exercícios resolvidos sobre volume do prisma
Resumo sobre volume do prisma
- Para calcular o volume do prisma, basta encontrar a área da base e multiplicar pela altura.
- A fórmula do volume de um prisma é: \(V=A_b\cdot h\)
- O prisma é um sólido geométrico com duas bases paralelas e congruentes.
- A base do prisma pode ter diferentes formatos: triângulo, quadrado, retângulo, pentágono, hexágono, entre outros.
- O primeiro passo para calcular o volume do prisma é identificar a forma da sua base.
- O princípio de Cavalieri permite comparar volumes de sólidos com a mesma altura e secções transversais equivalentes.
Videoaula sobre volume do prisma
Fórmula do volume do prisma
Para calcular o volume de um prisma qualquer, a fórmula é:
\(V=A_b\cdot h\)
- V: volume
- Ab: área da base
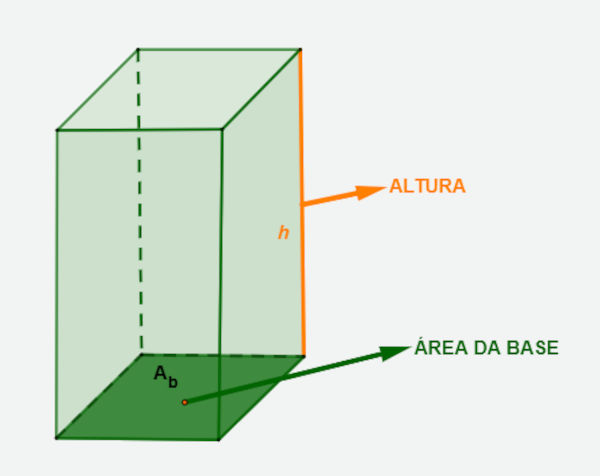
- h: altura do prisma
A altura do prisma é igual à distância entre as bases do prisma.
Como calcular o volume do prisma?
Para calcular o volume do prisma, sabemos que é necessário calcular a área da base, que depende do polígono que forma essa base, então: o primeiro passo é identificar a forma da base do prisma, posteriormente calculamos a área da base, e, por fim, multiplicamos pelo valor da altura.
→ Prisma triangular
Quando a base do prisma é um triângulo qualquer, utilizamos a fórmula da área do triângulo para calcular a área da base:
\(A_{\text{triângulo}} = \frac{b\cdot h}{2}\)
Um caso particular é quando a base do prisma é um triângulo equilátero, pois a fórmula para calcular a área de um triângulo equilátero é:
\(A_{\text{triângulo equilátero}} = \frac{l^2\sqrt3}{4}\)
- Exemplo:
Calcule o volume do prisma a seguir, sabendo que a sua base é um triângulo retângulo cuja medida dos catetos está indicada na imagem:
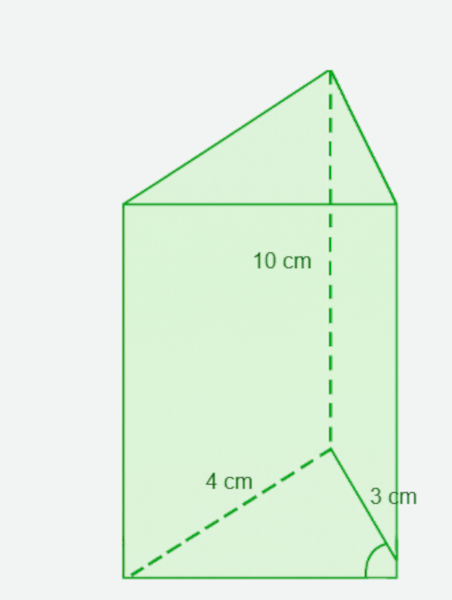
Resolução:
Sabemos que a base é um triângulo, então calculando a área da base, temos que:
\(A_b = \frac{b\cdot h}{2}\\ A_b = \frac{4\cdot 3}{2}\\ A_b = \frac{12}{2}\\ A_b = 6\)
Sabendo que a área da base mede 6 cm2, então o volume do prisma será:
\(V=A_b\cdot h\\ V= 6\cdot 10\\ V= 60\)
Então o volume desse prisma é 60 cm3.
- Exemplo 2:
Um prisma tem base formada por um triângulo equilátero de lados medindo 4 cm. Se sua altura mede 15 cm, então o volume desse prisma é igual a:
Resolução:
Como a base é um triângulo equilátero, então a área da base será:
\(A_b=\frac{l^2\sqrt3}{4}\\ A_b=\frac{4^2\sqrt3}{4}\\ A_b=\frac{16\sqrt3}{4}\\ A_b={4\sqrt3}\)
Agora calculando o volume, temos que:
\(V=A_b\cdot h\\ V= 4\sqrt3 \cdot 15\\ V= 60\sqrt3\ cm^3\)
→ Prisma de base quadrangular

Quando a base do prisma é um quadrilátero, ele é conhecido como prisma de base quadrangular. Nesse caso, a área da base do prisma é igual ao produto entre a base e a altura.
- Exemplo:
Calcule o volume do prisma a seguir:
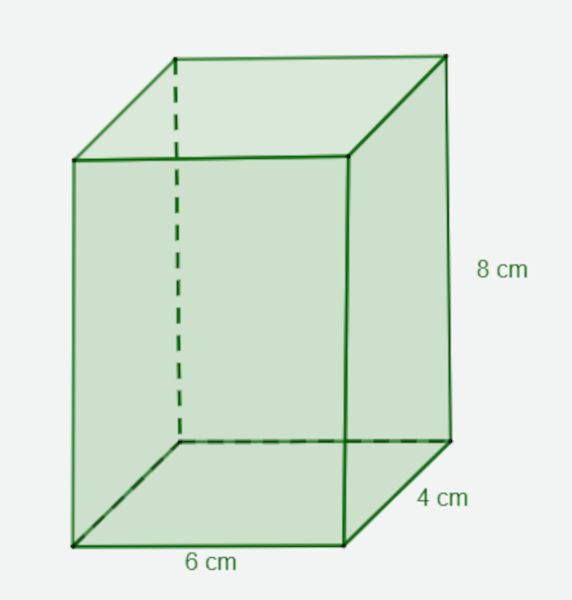
Resolução:
Calculando primeiro a área da base, temos que:
\(A_b=6\cdot 4=24 \)
Agora calculando o volume:
\(V=A_b\cdot h = 24\cdot 8 = 192\ cm^3\)
Então o volume do prisma é 192 cm3.
→ Prisma de base pentagonal
Para o prisma de base pentagonal, quando a sua base é um pentágono regular, a área da base pode ser calculada pela fórmula:
\(A_b = \frac{5 \cdot l \cdot a}{2}\)
- l: é a medida do lado do pentágono.
- a: é a medida do apótema do pentágono.

- Exemplo:
Considere um prisma pentagonal, com base de pentágono regular de 6 cm de lado e 7 cm de apótema, e com 10 cm de altura, então seu volume será de:
Resolução:
Calculando a área da base, temos que:
\(A_b = \frac{5 \cdot 6 \cdot 7}{2} \\ A_b = \frac{30 \cdot 7}{2} \\ A_b = \frac{210}{2} \\ A_b = 105 \\ \)
Então calculando o volume:
\(V = A_b \cdot h \\ V = 105 \cdot 10 \\ V = 1050\ \text{cm}^3 \\ \)
→ Prisma de base hexagonal
Para o prisma de base hexagonal, quando a sua base é um hexágono regular, a área da base pode ser calculada pela fórmula:
\(A_b = \frac{3l^2 \sqrt{3}}{2} \\ \)
- l: lado da base do hexágono.

- Exemplo:
Um prisma de base hexagonal tem lado base medindo 4 cm e altura medindo 8 cm, então a medida do seu volume é de:
Resolução:
Calculando a área da base:
\(A_b = \frac{3 \cdot 4^2 \sqrt{3}}{2} \\ A_b = \frac{3 \cdot 16 \sqrt{3}}{2} \\ A_b = \frac{48 \sqrt{3}}{2} \\ A_b = 24 \sqrt{3} \\ \)
Por fim, calculando o volume:
\(V = A_b \cdot h \\ V = 24 \sqrt{3} \cdot 8 \\ V = 192 \sqrt{3}\ \text{cm}^3 \\ \)
Veja também: O que é um paralelogramo?
O que é um prisma?
O prisma é um sólido geométrico que tem duas faces paralelas congruentes formadas por um polígono e faces laterais formadas por paralelogramos. Existem diferentes tipos de prisma, e o seu nome é determinado de acordo com o polígono que forma a sua fase, por exemplo: prisma de base triangular, prisma de base quadrangular, prisma de base pentagonal, e prisma de base hexagonal.

Princípio de Cavalieri
Princípio de Cavalieri foi criado com o objetivo de facilitar a compreensão e a determinação do volume de sólidos. Antigamente, calcular volumes era uma tarefa bastante complexa. No entanto, com esse princípio, tornou-se possível deduzir fórmulas para diversos sólidos geométricos por meio da comparação com formas mais simples, como prismas e cilindros.
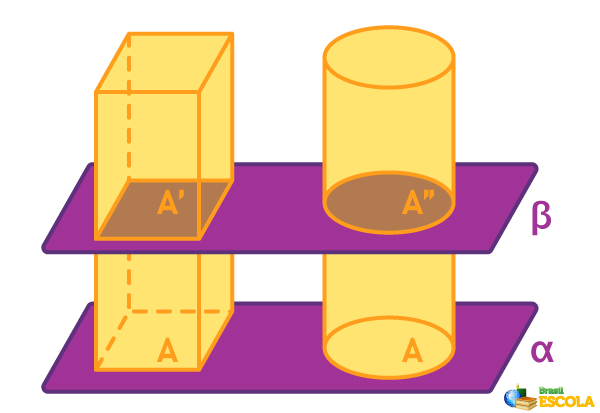
Cavalieri observou que, se dois sólidos têm a mesma altura e todas as suas seções paralelas à base têm áreas iguais em cada nível correspondente, então esses sólidos ocupam o mesmo volume, independentemente de suas formas externas.
Saiba mais: Como calcular o volume de um cilindro?
Exercícios resolvidos sobre volume do prisma
Questão 1
(Enem) Uma fábrica comercializa chocolates em uma caixa de madeira, como na figura.

A caixa de madeira tem a forma de um paralelepípedo reto-retângulo cujas dimensões externas, em centímetro, estão indicadas na figura. Sabe-se também que a espessura da madeira, em todas as suas faces, é de 0,5 cm.
Qual é o volume de madeira utilizado, em centímetro cúbico, na construção de uma caixa de madeira como a descrita para embalar os chocolates?
A) 654.
B) 666.
C) 673.
D) 681.
E) 693.
Resolução:
Alternativa C
É necessário calcular a diferença entre o volume interno e o volume externo. Como a caixa é um prisma de base retangular, temos que:
\(V_e = 20 \cdot 8 \cdot 20 = 3200 \\ V_i = 19 \cdot 7 \cdot 19 = 2527 \\ \)
Calculando a diferença:
\(V=3200-2527=673 cm^3\)
Questão 2
Kárita trabalha em uma fábrica de velas artesanais. Ela recebeu um pedido especial para produzir uma vela em formato de prisma hexagonal regular. O molde da vela tem base hexagonal regular com 6 cm de lado e 10 cm de altura. (\(\text{Use} \ \sqrt 3=1,73 \))
A) 519,6 cm3
B) 648,0 cm3
C) 720,5 cm3
D) 820,0 cm3
E) 934,2 cm3
Resolução:
Alternativa E
Calculando a área da base:
\(A_b = \frac{3 \cdot 6^2 \cdot \sqrt{3}}{2} = \frac{3 \cdot 36 \sqrt{3}}{2} \\ A_b = 54 \sqrt{3} \\ A_b = 54 \cdot 1{,}73 \\ A_b = 93{,}42\ \text{cm}^2 \\ \)
Então o volume será:
\(V = A_b \cdot h \\ V = 93{,}42 \cdot 10 \\ V = 934{,}2\ \text{cm}^3 \\ \)


