Área do prisma

Prismas são figuras tridimensionais formadas por duas bases congruentes e paralelas, as bases, por sua vez, são formadas por polígonos convexos. As outras faces que recebem o nome de faces laterais são formadas por paralelogramos. Para determinar a área de um prisma, é necessário antes realizar sua planificação e, em seguida, calcular a área da figura planificada.

Leia também: Diferenças entre figuras planas e espaciais

Tópicos deste artigo

• 1 - Planificação de um prisma
• 2 - Cálculo da área lateral
  • Exemplo
• 3 - Cálculo da área base
  • Exemplo
• 4 - Cálculo da área total
  • Exemplo
• 5 - Exercícios resolvidos

Planificação de um prisma

A ideia da planificação é transformar uma figura de três dimensões em uma figura de duas dimensões. Na prática seria o equivalente a cortar sobre as arestas do prisma. Veja a seguir o exemplo de planificação de um prisma triangular.

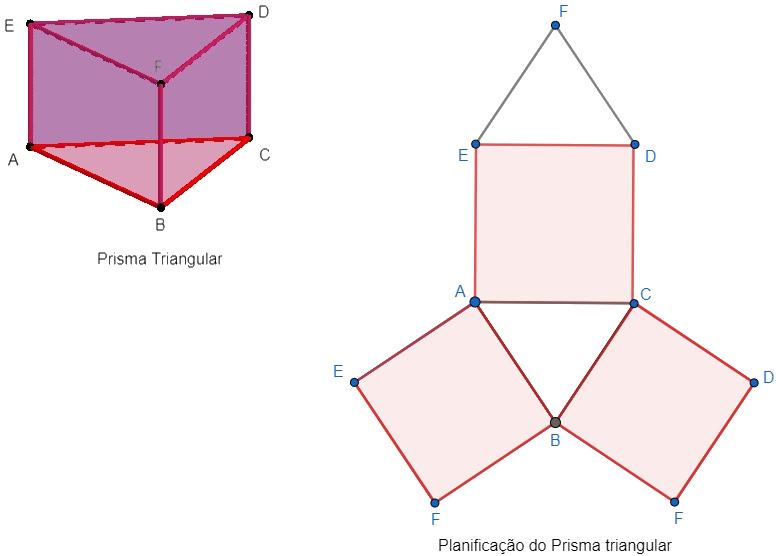
O mesmo processo pode ser adotado para todo prisma, entretanto, veja que, à medida que aumentamos o número de lados dos polígonos da base, a tarefa fica cada vez mais difícil. Por esse motivo, faremos as generalizações com base na planificação desse polígono.

Cálculo da área lateral

Observando a imagem do prisma triangular, temos que os paralelogramos ABFC, ABFD e ACDE são as faces laterais. Note que as faces laterais de um prisma sempre serão paralelogramos independentemente do número de lados dos polígonos da base, isso acontece, pois elas são paralelas e congruentes.

Observando a figura do prisma triangular, vemos também que temos três faces laterais. Isso ocorre por conta do número de lados do polígono da base, ou seja, se as bases do prisma forem um quadrilátero, teremos quatro faces laterais, se as bases forem um pentágono, teremos cinco faces laterais, e assim sucessivamente. Dessa forma: o número de lados do polígono da base afeta a quantidade de faces laterais do prisma.

Portanto, a área lateral (A_L) de qualquer prisma é dada pela área de uma face lateral multiplicada pela quantidade de faces laterais, ou seja, é a área do paralelogramo multiplicada pelo número de lados da face.

A_L = (base · altura) · número de lados da face

• Exemplo

Calcule a área lateral de um prisma hexagonal regular com aresta da base igual a 3 cm e altura igual a 11 cm.

O prisma em questão é representado por:

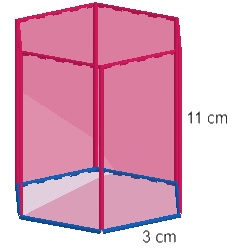
A área lateral então é calculada pela área do retângulo vezes a quantidade de lados do polígono da base, que é 6, logo:

A_L = (base · altura) · número de lados da face

A_L = (3 · 11) · 6

A_L = 198 cm²

Cálculo da área base

A área da base (A_B) de um prisma depende do polígono que a compõe. Como em um prisma temos duas faces paralelas e congruentes, a área da base é dada pela soma das áreas dos polígonos paralelos, isto é, duas vezes a área do polígono.

A_B = 2 · área do polígono

Leia também: Áreas de figuras planas

• Exemplo

Calcule a área da base do um prisma hexagonal regular com aresta da base igual a 3 cm e altura igual a 11 cm.

A base desse prisma é um hexágono regular, e esse, visto de cima, fica:

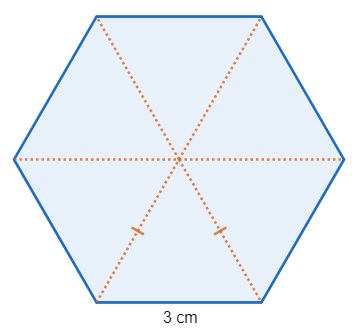
Observe que os triângulos formados no interior do hexágono são equiláteros, logo, a área do hexágono é dada por seis vezes a área do triângulo equilátero.

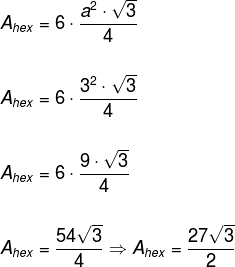
Entretanto observe que, no prisma, temos dois hexágonos, logo, a área da base é duas vezes a área do polígono.

Cálculo da área total

A área total (A_T) de um prisma é dada pela soma da área lateral (A_L) com a área da base (A_B).

A_T = A_L + A_B

• Exemplo

Calcule a área total do um prisma hexagonal regular com aresta da base igual a 3 cm e altura igual a 11 cm.

Dos exemplos anteriores, temos que A_L = 198 cm² e A_B = 27√3 cm². Logo, a área total é dada por:

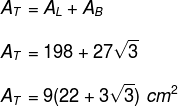
Exercícios resolvidos

Questão 1 – Um galpão tem o formato de um prisma que tem como base um trapézio, como mostra a figura.

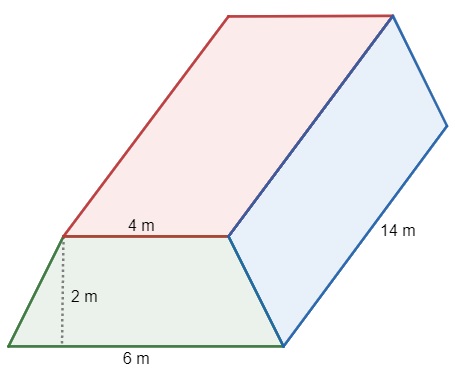
Deseja-se pintar esse galpão e sabe-se que o preço da tinta é de 20 reais por metro quadrado. Quanto será gasto para pintar esse galpão? (Dado: √2 = 1,4)

Solução

Inicialmente vamos determinar a área do galpão. Sua base é um trapézio, logo:

Portanto, a área da base é:

A_B = 2 ·A_trapézio

A_B = 2 ·10

A_B = 20 m²

            A área lateral em vermelho é um retângulo, e temos a parte de baixo, logo, essa área é:

A_V = 2 · 4· 14

A_V= 112 m²

A área em azul também é um retângulo, mas não temos sua base. Utilizando o teorema de Pitágoras no triângulo formado pelo trapézio, temos:

x² = 2² + 2²

x² = 8

x = 2√2

Assim a área do retângulo em azul é:

A_A = 2 ·14·2√2

A_A = 54√2 m²

Portanto, a área lateral do prisma é igual a:

A_L = 112 +  54√2

A_L = 112 + 75,6

A_L = 187,6 m²

E assim a área total desse prisma é:

A_T= 20 + 187,6

A_T= 207,6 m²

Como o preço da tinta é de 20 reais por metro quadrado, o valor gasto para pintar o galpão é:

20 ·207,6 = 4.152 reais

Resposta: O valor gasto para pintar o galpão é de R$ 4.152,00

Por Robson Luiz
Professor de Matemática