Área do cilindro

A área do cilindro, sólido geométrico formado por duas bases circulares paralelas e uma área lateral retangular, é igual à soma da área das duas bases mais a soma da área lateral do cilindro. Para calcular a área total do cilindro, utilizamos a seguinte fórmula: 2πr(r + h).

Leia também: Área da pirâmide — como calcular?

Tópicos deste artigo

• 1 - Resumo sobre área do cilindro
• 2 - Videoaula sobre área do cilindro
• 3 - O que é cilindro?
• 4 - Planificação do cilindro
• 5 - Fórmula da área da base do cilindro
• 6 - Fórmula da área lateral do cilindro
• 7 - Fórmula da área total do cilindro
• 8 - Exercícios resolvidos sobre área do cilindro

Resumo sobre área do cilindro

• O cilindro é o sólido geométrico que possui duas bases circulares.

• É considerado um corpo redondo.

• A área do cilindro é a soma da área da base com a área lateral.

• Para calcular a área da base do cilindro, utilizamos a fórmula:

\(A_b=\pi r^2\)

• Para calcular a área lateral do cilindro, a fórmula é:

\(A_l=2\pi rh\)

• A área total do cilindro é a soma da área das duas bases com a área lateral, logo ela é calculada pela fórmula:

\(A_T=2\pi r\left(r+h\right)\)

Videoaula sobre área do cilindro

O que é cilindro?

O cilindro é um sólido geométrico composto por duas faces formadas por círculos paralelas entre si e a área lateral que conecta essas duas faces. Por ser construído por meio da rotação de figuras planas e ter superfície curva, é considerado um corpo redondo.

Há vários objetos do nosso cotidiano com formato de cilindro, como copos, galões, embalagens, entre outros.

Planificação do cilindro

Para compreender o cálculo da área do cilindro, antes é importante entender a planificação desse sólido geométrico.

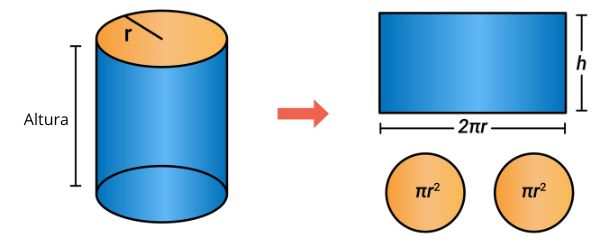
Note que o cilindro é composto por duas bases circulares de raio r e um retângulo que possui base medindo 2πr e altura medindo h.  Para calcular a área do cilindro, é necessário calcular a área da base e a área lateral do cilindro.

Acesse também: Planificação de sólidos geométricos — as planificações dos sólidos geométricos mais conhecidos

Fórmula da área da base do cilindro

Para calcular a área da base do cilindro, basta lembrar que ela é um círculo de raio r. Para o cálculo, utilizamos a fórmula da área do círculo. Logo, a área da base do cilindro pode ser calculada pela fórmula:

\(A_b=\pi r^2\)

• r: raio do cilindro.

Exemplo:

Um cilindro possui raio medindo 4 cm, então a área da base desse cilindro é de:

\(A_b=\pi r^2\)

\(A_b=\pi\cdot4^2\)

\(A_b=16\pi\ cm²\)

Fórmula da área lateral do cilindro

A área lateral do cilindro é formada por um retângulo que possui lados medindo h e 2πr, sendo que h é a altura do cilindro e r é o raio da base da circunferência. Logo, utiliza-se a fórmula da área do retângulo. A área do retângulo é igual ao produto entre a sua base e a sua altura, portanto a área lateral do cilindro é calculada por:

\(A_l=2\pi rh\)

• r: comprimento do raio do cilindro.

• h: comprimento da altura do cilindro.

Exemplo:

A área lateral de um cilindro que possui altura medindo 8 cm e raio da base igual a 3 cm é de:

\(A_l=2\pi rh\)

\(A_l=2\pi\cdot3\cdot8\)

\(A_l=2\pi\cdot24\)

\(A_l=48\pi\ cm²\)

Fórmula da área total do cilindro

A área total do cilindro, conhecida também apenas como área do cilindro, é igual à soma da área das bases com a área lateral do cilindro. Sabemos que as duas bases são iguais, logo basta fazer a multiplicação da área da base por 2 e somar com a área lateral para encontrarmos o valor:

\(A_T=2A_b+A_l\)

Então, conhecendo a fórmula da área da base e a fórmula da área lateral do cilindro, temos que:

\(A_T=2\pi r^2+2\pi rh\)

Note que 2πr aparece nas duas parcelas, logo podemos colocar esse termo em evidência, gerando uma fórmula mais prática para a área do cilindro:

\(A_T=2\pi r\left(r+h\right)\)

Exemplo:

Um determinado cilindro possui 4 cm de raio e 12 cm de altura, então sua área total é de:

\(A_T=2\pi r\left(r+h\right)\)

\(A_T=2\pi\cdot4\ \left(4+12\right)\)

\(A_T=2\pi\cdot4\cdot16\)

\(A_T=8\pi\cdot16\)

\(A_T=128\pi\)

Veja também: Área do trapézio — como calcular?

Exercícios resolvidos sobre área do cilindro

Questão 1

Qual é a área total de um cilindro com altura de 9 cm e cujo raio da base é de 6 cm?

(Utilize π = 3.)

A) 610 cm²

B) 540 cm²

C) 490 cm²

D) 420 cm²

E) 380 cm²

Resolução:

Alternativa B

Calculando a área total, temos que:

\(A_T=2\pi r\left(r+h\right)\)

\(A_T=2\cdot3\cdot6\left(6+9\right)\)

\(A_T=36\cdot15\)

\(A_T=540\ cm^2\)

Questão 2

Um galão será construído no formato de cilindro com 659,4 cm² de plástico. Utilizando π = 3,14, qual deve ser a altura desse galão, sabendo que seu raio é de 5 cm?

A) 12 cm

B) 13 cm

C) 14 cm

D) 15 cm

E) 16 cm

Resolução:

Alternativa E

Sabemos que \(A_T=659,4\ cm^2\), portanto:

\(A_T=2\pi r\left(r+h\right)\)

\(659,4=2\cdot3,14\cdot5\left(5+h\right)\)

\(659,4=31,4\left(5+h\right)\)

\(\frac{659,4}{31,4}=5+h\)

\(21=5+h\)

\(21-5=h\)

\(h=16\ cm\)

 

Por Raul Rodrigues de Oliveira
Professor de Matemática