Os corpos redondos, também chamados de sólidos de revolução, são objetos de estudo da geometria espacial. Eles são sólidos geométricos que possuem superfícies arredondadas e estão bastante presente no nosso dia a dia, em objetos como uma bola de futsal, um chapéu de aniversário, uma lata de refrigerante etc.
Os sólidos geométricos considerados corpos redondos são a esfera, o cilindro e o cone. Cada um deles possui fórmulas específicas para o cálculo de sua área total e volume.
Leia também: Diferenças entre figuras planas e espaciais
Tópicos deste artigo
- 1 - O que são corpos redondos?
- 2 - Quais são os corpos redondos?
- 3 - Poliedros e corpos redondos
- 4 - Exercícios resolvidos
O que são corpos redondos?

Chamamos de corpos redondos os sólidos geométricos que possuem suas superfícies curvas. Eles também são conhecidos como sólidos de revolução, por serem construídos a partir da rotação de uma figura plana.
Os corpos redondos são bastante presentes no nosso dia a dia, é possível percebê-los numa lata de refrigerante, que possui o formato cilíndrico; numa bola de futebol, que possui formato esférico; e também num chapéu de festa infantil ou nos cones utilizados pelo departamento de trânsito possuem formatos de cone.
Quais são os corpos redondos?
-
Cone
O cone é um sólido de revolução caracterizado por ter um círculo como base. Esse sólido geométrico é construído a partir da rotação de um triângulo. Um cone pode ser reto, quando a sua altura fica no centro da circunferência que forma a base, ou oblíquo, quando a sua altura não coincide com o centro da base.

Para calcular o volume de um cone, é necessário conhecermos o raio da base e a sua altura.
Como a base é sempre um círculo, podemos calcular a área da base por
Ab= πr²
O volume do cone é a terça parte da multiplicação entre a área da base e a altura:
![]()
Conhecendo a planificação de um cone, calcular a área total é somar a área lateral com a área da base.
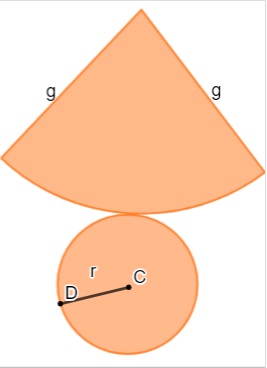
Como a base do cone é um círculo, a área da base é calculada a partir da fórmula:
Ab= πr²
Para calcular a área lateral, precisamos conhecer ou encontrar o valor da geratriz g do cone. Ela pode ser calculada pelo teorema de Pitágoras:
g² = r²+ h²
Já a área lateral que é um setor circular é calculada por:
Al=π·r·g
Então, a área total do cone é a soma de Ab + Al:
AT = πr(r + g)
Veja também: O que é um tronco de cone?
-
Cilindro
O cilindro é caracterizado por ter duas bases circulares de mesmo raio. Assim como o cone, o cilindro pode ser classificado como reto ou oblíquo.

Para calcular o volume do cilindro, precisamos conhecer o valor da sua altura e o comprimento do raio de sua base:
V = πr²·h
Para calcular a área total, é necessário calcular a área da base e a área lateral.
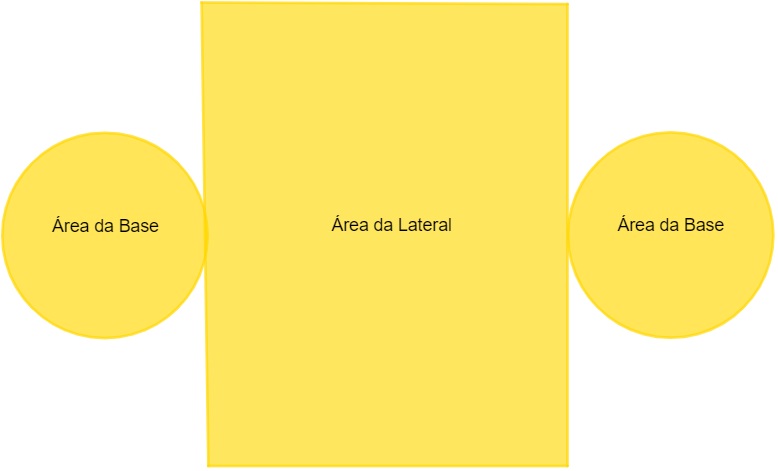
AT = 2Ab + AL
Como a base é um círculo, então:
Ab= πr²
Já a área lateral é um retângulo que possui base igual ao comprimento do círculo e altura h, logo a área lateral é:
AL= 2πrh
Substituindo na área total, podemos calcular essa área pela fórmula:
AT = 2πr (r + h)
-
Esfera
Diferente dos sólidos anteriores, a esfera não possui uma base circular. Ela é construída a partir da rotação de uma semicircunferência.

Para calcular o volume da esfera é necessário conhecer somente o raio:
![]()
Já a área total da esfera pode ser calculada por:
AT = 4πr²
Acesse também: Quais são os elementos da esfera?
Poliedros e corpos redondos
A geometria espacial separa os sólidos geométricos em dois grupos de igual importância, um deles são os corpos redondos que vimos durante o texto, os outros são os poliedros, que são sólidos geométricos cujo as faces são polígonos.
São poliedros, por exemplo, os paralelepípedos e as pirâmides. Os sólidos que não se enquadram em nenhum desses conjuntos são conhecidos como outros sólidos.

Exercícios resolvidos
Questão 1 - (UDESC 2015) Uma bola esférica é composta por 24 faixas iguais, como indica a figura.
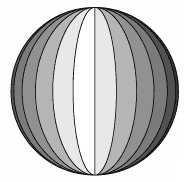
Sabendo-se que o volume da bola é de 2304 π cm³ então a área da superfície de cada faixa é de:
A)20π cm²
B)24π cm²
C)28π cm²
D)27π cm²
E)25π cm²
Resolução
Alternativa B
1º Passo: Encontrar o raio da esfera.
Conhecendo o volume, vamos calcular o raio da esfera.
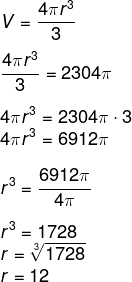
2º passo: calcular a área total, sabendo que o raio mede 12 cm.
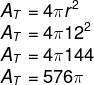
3º passo: calcular a área de uma faixa.
576π : 24 = 24π cm²
Questão 2 – Qual é a razão entre o volume de um cone e o volume de um cilindro que possuem a mesma altura?
A) 1/3
B) 2/3
C) 3/1
D) 3/2
E) 1/6
Resolução
Alternativa A
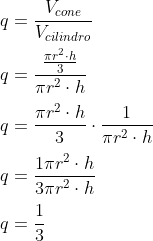
Por Raul Rodrigues de Oliveira
Professor de Matemática

