Pirâmide

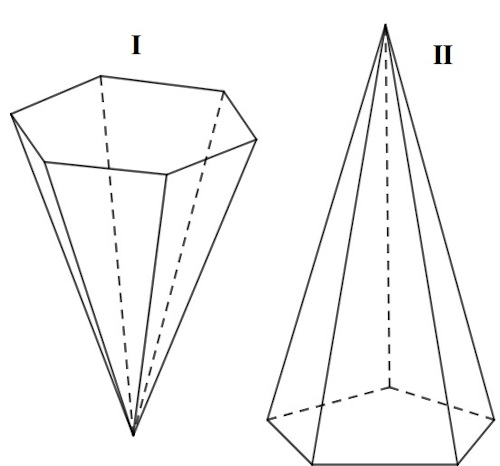
Pirâmides são figuras geométricas que aparecem com frequência, principalmente na arquitetura. As pirâmides são sólidos geométricos  construídos no espaço com base em um polígono no plano e um ponto fora desse plano. Por tratar-se de uma figura tridimensional, é possível calcular o seu volume, além disso, podemos planificá-la e assim encontrar sua área.

Leia mais: Ponto, reta, plano, espaço: conceitos básicos da geometria espacial

Tópicos deste artigo

• 1 - O que é pirâmide?
• 2 - Elementos de uma pirâmide
• 3 - Tipos de pirâmides
• 4 - Área da pirâmide
  • • Exemplo
• 5 - Volume da pirâmide

O que é pirâmide?

Considere um polígono convexo contido em um plano e um ponto H que não pertence ao plano. Definimos a pirâmide como sendo a união de todos os vértices do polígono convexo no ponto H.

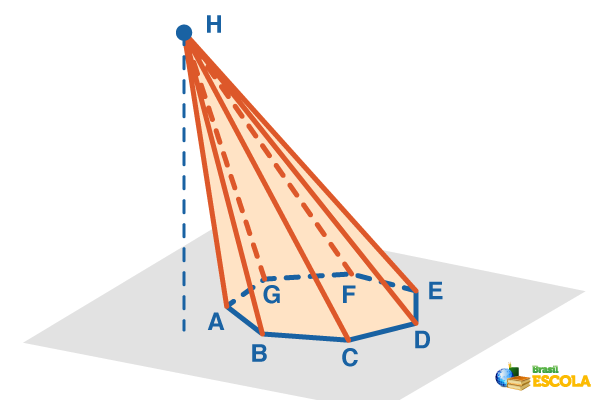
Elementos de uma pirâmide

Considere a pirâmide a seguir.

• Base da pirâmide: polígono ABCDEF.
• Vértice da pirâmide: ponto H.
• Faces laterais: AHB, BHC, CHD, DHE, EHF e FHA, que são os triângulos formados pela união do vértice da pirâmide com os vértices do polígono.
• Arestas da base: AB, BC, CD, DE, EF e FA, que são os lados da base.
• Arestas laterais: AH, BH, CH, DH, EH e FH, que são os segmentos das faces laterais.
• Altura da pirâmide: h, que é a distância entre o vértice da pirâmide e a base.

Vamos estabelecer as notações para alguns elementos:

• A área da base será denotada por A_b.
• A área de uma face lateral será representa por A_F.
• O somatório das áreas das faces é chamado de área lateral, e essa é denotada por A_L.

Assim, a área total da pirâmide é dada pela soma da área da base (A_b) com a área lateral (A_L) e é denotada por A_T, ou seja:

A_T = A_b + A_L

Saiba mais: Tronco da pirâmide: saiba o que é e como calcular sua área

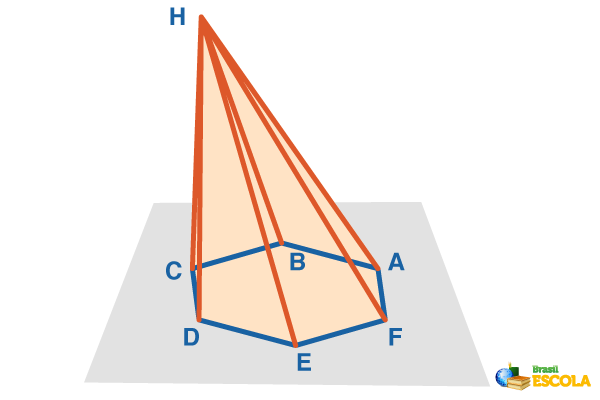
Tipos de pirâmides

Do mesmo modo como nomeamos os prismas de acordo com o polígono da base, nomeamos também as pirâmides seguindo essa ideia. Por exemplo, se uma pirâmide possui na base um triângulo, ela é chamada de pirâmide de base triangular, agora, se uma pirâmide possui como base um quadrilátero, é chamada de pirâmide de base quadrangular, e assim sucessivamente.

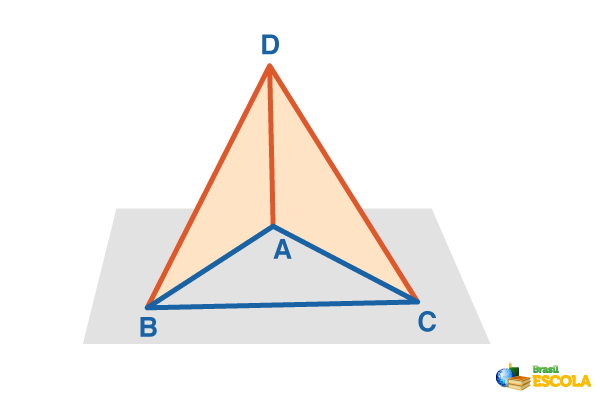
As pirâmides também se dividem em dois grupos: retas e oblíquas. As pirâmides retas são assim chamadas quando a projeção do vértice coincide com o centro da base, caso contrário elas são ditas oblíquas. Veja os exemplos a seguir:

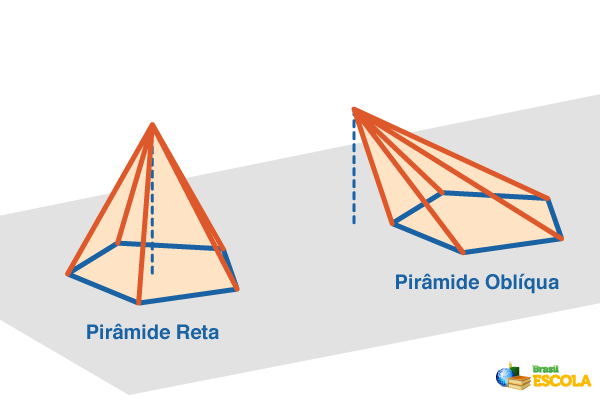
Se em uma pirâmide reta a base for um polígono regular, então a pirâmide será regular. Nesse tipo, a distância do vértice até o centro da base é a altura da pirâmide.

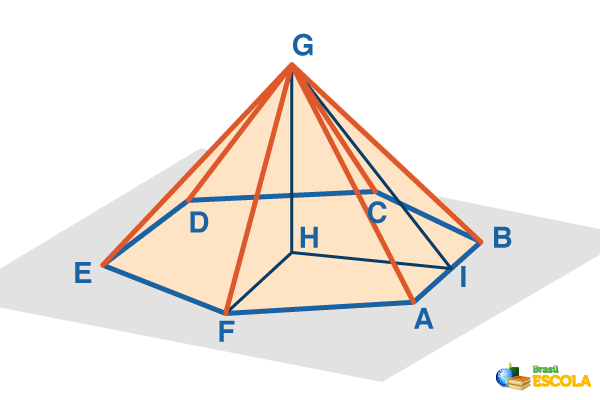
O segmento que une o vértice da pirâmide com o ponto médio de uma aresta da base é chamado de apótema da pirâmide, nesse caso GI. Já o segmento que une o centro da base ao ponto médio de uma aresta da base é chamado de apótema da base, nesse caso HI.

Observe os triângulos GHI e GHF e note que eles são triângulos retângulos, logo, nele o teorema de Pitágoras é valido. Assim:

(GI)² = (GH)² + (HI)²

(GF)² = (GH)² + (HF)²

Área da pirâmide

A área da pirâmide é dada pela soma das áreas laterais e a área da base, isto é:

A_T = A_b + A_L

A não existência de uma fórmula específica dá-se pelo fato de pirâmides terem bases diferentes. Na expressão anterior, perceba que a área total A_T depende do valor da área da base. Veja alguns exemplos.

• Exemplo

Calcule a área total de uma pirâmide reta, cuja base é um quadrado de lado 10 m e a altura de uma face lateral é igual a 13 m.

Solução

Inicialmente desenharemos a pirâmide de acordo com os dados do exercício.

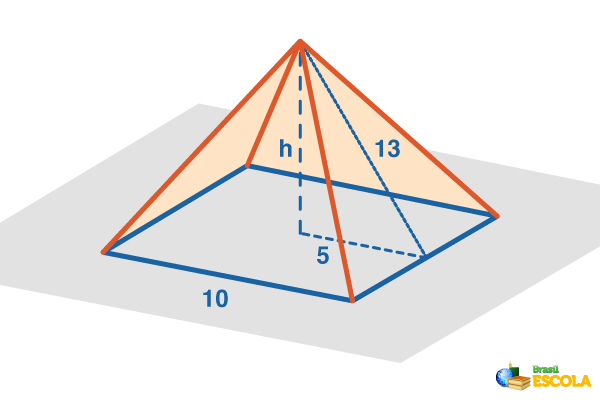
Note que podemos calcular a área da face com os dados fornecidos utilizando a fórmula da área do triângulo. 

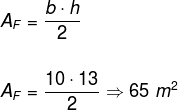
Como temos quatro faces, a área lateral é igual a 65 · 4 = 260 m².

Agora, devemos calcular a área da base que é um quadrado, logo:

Portanto, a área da pirâmide é a soma da área lateral com a área da base.

A_T = A_b + A_L

A_T = 100 + 260

A_T = 360 m²

Leia também: Área de figuras planas: saiba como calcular diversos tipos

Volume da pirâmide

Considere uma pirâmide de altura h.

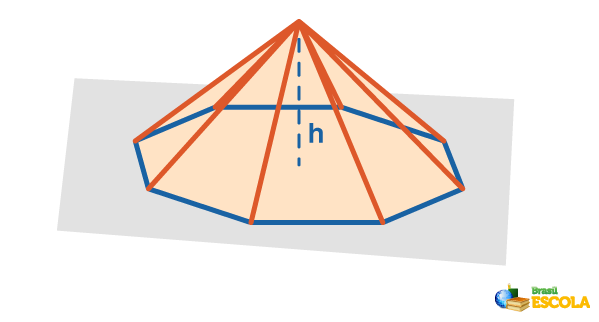
O volume da pirâmide é dado pela terça parte do produto da área da base (A_b) e altura (h):

• Exemplo

(Enem) Artur e Bernardo foram acampar e cada um levou uma barraca. Ambas têm a forma de uma pirâmide de base quadrada, com as arestas laterais congruentes. A barraca de Bernardo tem a altura e as arestas laterais 10% maiores em relação à de Artur. Assim, a razão entre os volumes das barracas de Bernardo e Artur, nessa ordem, é:

a) 1,1

b) 1,21

c) 1,331

d) 1,4641

e) 1,5

Solução

Inicialmente, calcularemos o volume da barraca de Artur, aqui denotada por V_A. Como a base da pirâmide é um quadrado, sua área é a medida do lado ao quadrado, vamos representá-la por L².

Agora vamos determinar o volume da barraca de Bernardo, representada por V_B. Antes note que a altura e as arestas são 10% maiores em relação à barraca de Artur, logo, temos que:

h_B = h + 10% de h

h_B = h + 0,1 · h

h_B = 1,1 · h

Do mesmo modo para a área da base:

A_B = (1,1)² · L²

Logo, a área da barraca de Bernardo é:

Como o objetivo do exercício é encontrar a razão entre os volumes das barracas de Bernardo e de Artur, temos que:

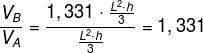
Perceba que podemos “cortar” a fração L² · h sobre 3, pois representa o mesmo número.

Alternativa C

Por Robson Luiz
Professor de Matemática