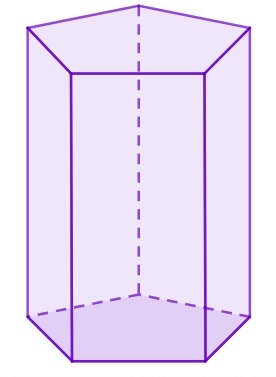
Poliedros

Poliedros (do latim poli — muitos — e edro — face) são figuras tridimensionais formadas pela união de polígonos regulares, na qual os ângulos poliédricos são todos congruentes. A união desses polígonos forma elementos que compõem o poliedro, são eles: vértices, arestas e faces. No entanto, nem toda figura tridimensional é um poliedro, um exemplo disso são as figuras que possuem faces curvas chamadas de corpos redondos.

Existe uma fórmula matemática que relaciona os elementos de um poliedro chamada relação de Euler. Além disso, os poliedros dividem-se em dois grupos: os chamados poliedros convexos e os não convexos. Alguns poliedros merecem uma atenção especial, são os chamados poliedros de Platão: tetraedro, hexaedro, octaedro, dodecaedro e icosaedro.

Leia também: Diferenças entre figuras planas e espaciais

Tópicos deste artigo

• 1 - Poliedros convexos
• 2 - Elementos de um poliedro convexo
• 3 - Propriedades de um poliedro convexo
  • Propriedade 1
  • Propriedade 2
• 4 - Poliedros côncavos (não convexos)
• 5 - Poliedros regulares
• 6 - Relação de Euler
  • Tetraedro regular
  • Hexaedro regular
  • Octaedro regular
  • Dodecaedro regular
  • Icosaedro regular
• 7 - Exercícios resolvidos

Poliedros convexos

Um poliedro será convexo quando for formado por polígonos convexos, de forma que as condições a seguir sejam aceitas:

1. Dois dos polígonos nunca são coplanares, ou seja, não pertencem ao mesmo plano.
2. Cada lado de um desses polígonos pertence a apenas dois polígonos.
3. O plano que contém qualquer um desses polígonos deixa os demais polígonos no mesmo semiespaço.

Leia também: Soma dos ângulos internos e externos de um polígono convexo

Elementos de um poliedro convexo

Considere este poliedro convexo:

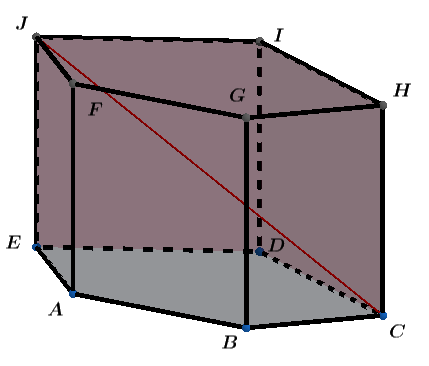
Os quadriláteros na figura são chamados de faces do poliedro.

Os pentágonos são as faces e a base do poliedro, que recebe o nome de poliedro de base pentagonal.

Os segmentos que formam cada uma das faces são denominados arestas do poliedro.

Os pontos em que as arestas encontram-se são denominados vértices.

O segmento de reta JC será denominado diagonal do poliedro, denotada por:

JC é uma das diagonais, entendemos diagonal do poliedro como sendo o segmento de reta que une dois vértices não pertencentes à mesma face.

Temos também o ângulo poliédrico, formado entre as arestas, denotado por:

Um ângulo poliédrico é chamado de triédrico quando três arestas têm origem em um vértice. Da mesma forma, é chamado de tetraédrico, caso quatro arestas tenham origem em um vértice, e assim por diante.

Daqui em diante, estabeleceremos algumas notações, são elas:

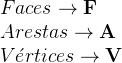
Saiba mais: Planificação de sólidos geométricos

Propriedades de um poliedro convexo

• Propriedade 1

A soma das arestas de todas as faces é igual ao dobro do número de arestas do poliedro.

Exemplo

Um poliedro tem 6 faces quadradas. Vamos determinar a quantidade de arestas.

De acordo com a propriedade, basta multiplicar o número de arestas de uma face pela quantidade de faces, e isso é igual ao dobro do número de arestas. Dessa forma:

• Propriedade 2

A soma dos vértices de todas as faces é igual à soma das arestas de todas as faces, que é igual ao dobro do número de arestas.

Exemplo

Um poliedro com 5 ângulos tetraédricos e 4 ângulos hexaédricos. Vamos determinar a quantidade de arestas.

De maneira análoga ao exemplo anterior, a segunda propriedade diz que a soma das arestas de todas as faces é igual ao dobro do número de arestas. O número de arestas é dado pelo produto de 5 por 4 e 4 por 6, pois são 5 ângulos tetraédricos e 4 hexaédricos. Assim:

Poliedros côncavos (não convexos)

Um poliedro é não convexo, ou côncavo, quando tomamos dois pontos em faces distintas e a reta r que contém esses pontos não fica toda contida no poliedro.

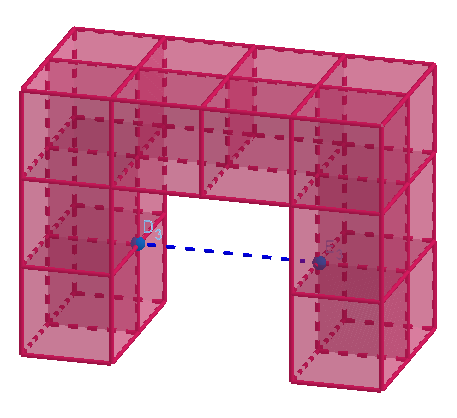
Perceba que a reta (em azul) não está por completa no poliedro, assim o poliedro (em rosa) é côncavo ou não convexo.

Poliedros regulares

Dizemos que um poliedro é regular quando suas faces são polígonos regulares iguais entre si e com os ângulos poliédricos todos iguais.

Veja alguns exemplos:

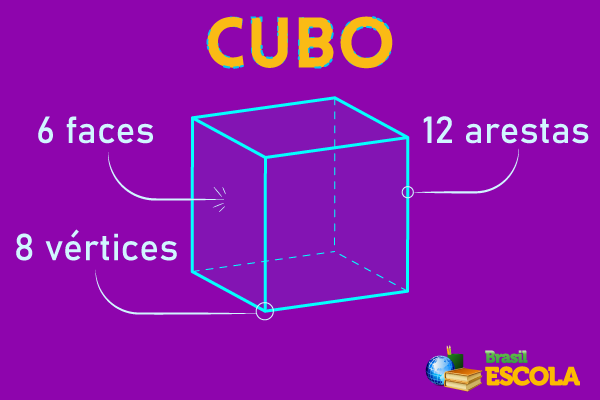
Perceba que todas as suas faces são polígonos regulares. Suas faces são formadas por quadrados e as arestas são todas congruentes, ou seja, possuem a mesma medida.

Leia também: O que são polígonos regulares e convexos?

Relação de Euler

Também conhecido como teorema de Euler, o resultado foi provado por Leonhard Euler (1707 - 1783) e garante que em todo poliedro convexo fechado é válida a seguinte relação:

Poliedros de Platão

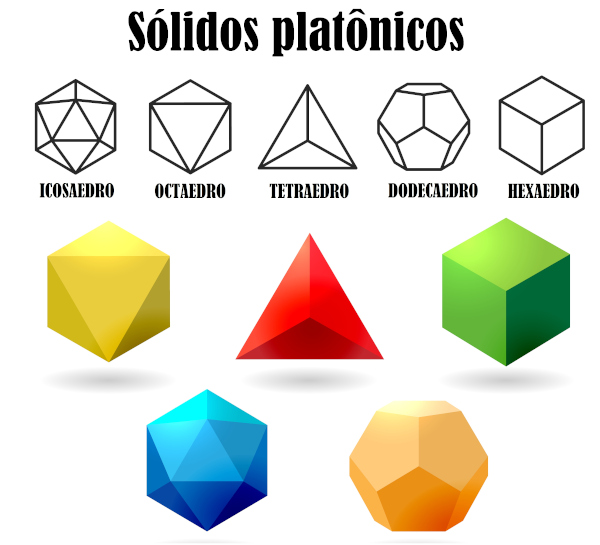
É chamado de poliedro de Platão todo poliedro que satisfaz as condições seguintes:

1. É valida a relação de Euler

2. Todas as faces apresentam o mesmo número de arestas

3. Todos os ângulos poliédricos possuem o mesmo número de arestas

É provado que existem somente cinco poliedros regulares e convexos, ou poliedros de Platão, são eles:

• Tetraedro regular

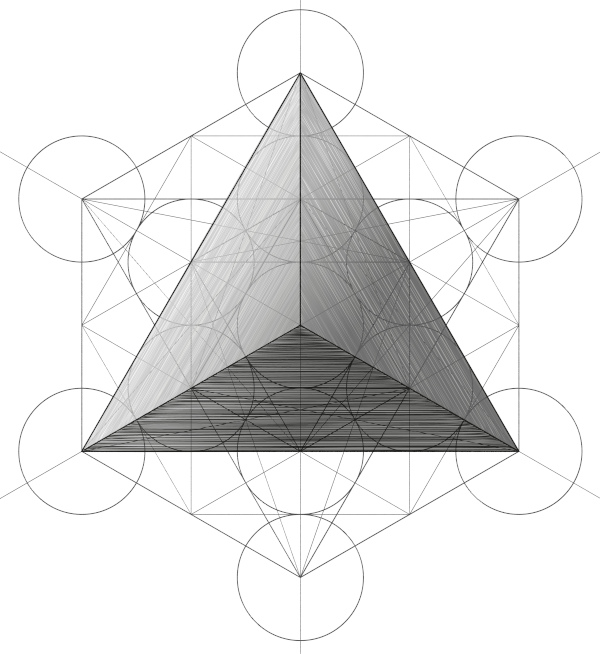
O tetraedro possui 4 faces triangulares congruentes e 4 ângulos triédricos congruentes.

• Hexaedro regular

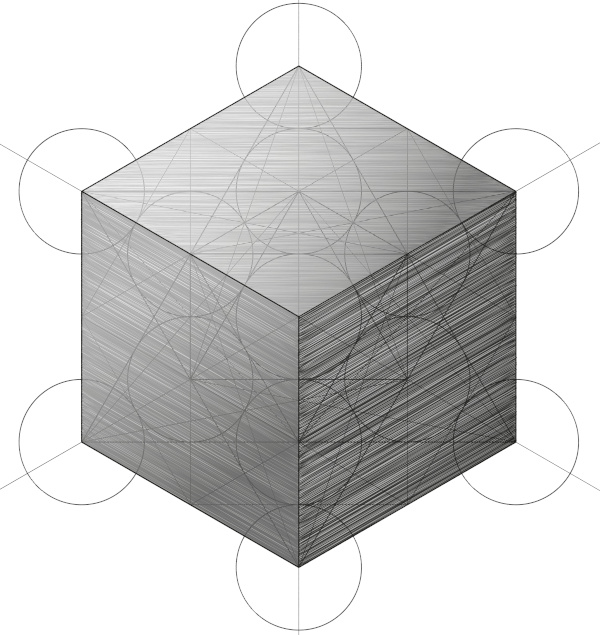
O hexaedro possui 6 faces quadrangulares congruentes e 8 ângulos triédricos congruentes.

• Octaedro regular

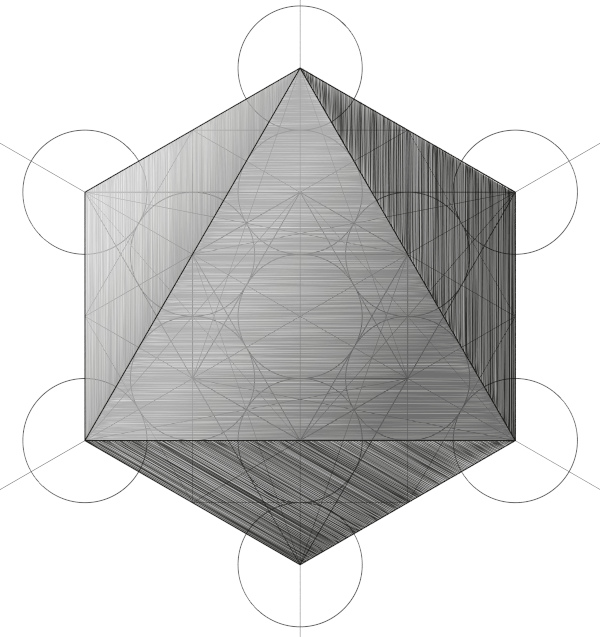
O octaedro possui 8 faces triangulares congruentes e 6 ângulos tetraédricos congruentes.

• Dodecaedro regular

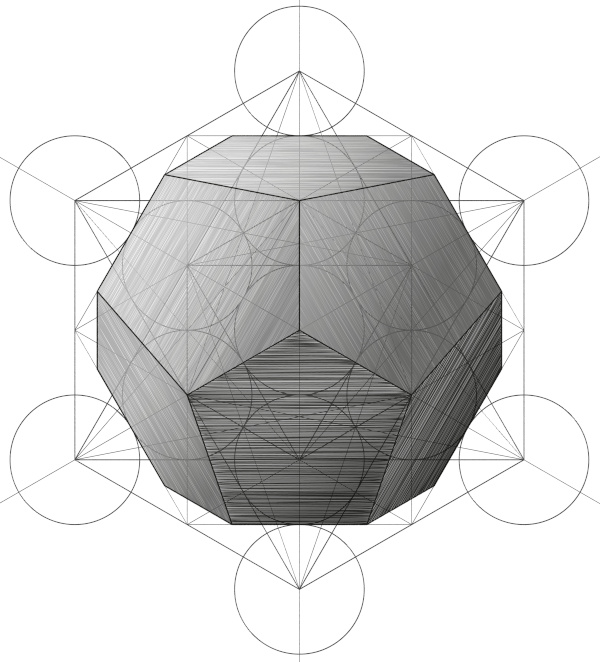
O dodecaedro possui 12 faces pentagonais congruentes e 20 ângulos triédricos congruentes.

• Icosaedro regular

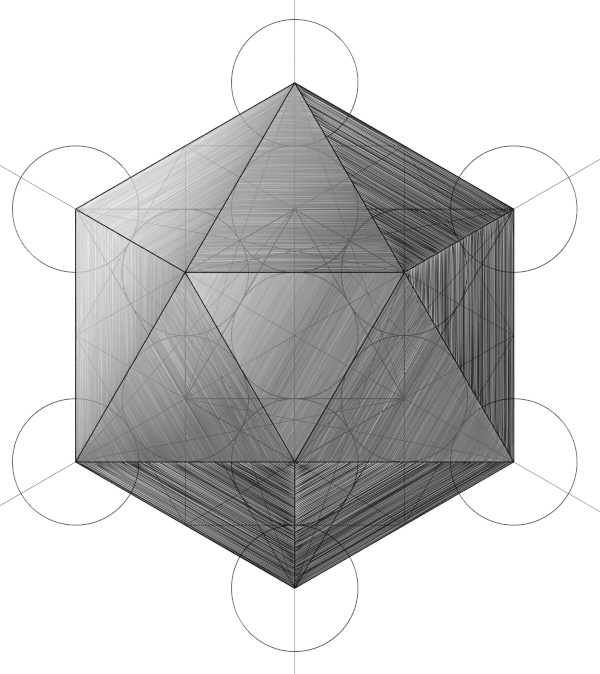
O icosaedro possui 20 faces triangulares congruentes e 12 ângulos pentaédricos congruentes.

Exercícios resolvidos

1) (Enem) Uma joia foi lapidada na forma de um poliedro convexo de 32 faces, sendo que 20 dessas são hexaedros e as restantes são pentagonais. Essa joia será um presente para uma senhora que está fazendo aniversário, completando uma idade cujo número é a quantidade de vértices desse poliedro. Essa senhora está completando:

a) 90 anos

b) 72 anos

c) 60 anos

d) 56 anos

e) 52 anos

Solução:

Da propriedade 1 de poliedros convexos sabemos que:

Agora, como conhecemos o número de arestas e o número de faces, podemos utilizar a relação de Euler.

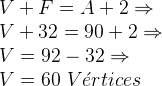
Como a idade que a senhora está completando é igual ao número de vértices, então essa é de 60 anos. Alternativa c.

2) (PUC-SP) Quantas arestas tem um poliedro convexo de faces triangulares em que o número de vértices é três quintos do número de faces?

a) 60

b) 30

c) 25

d) 20

e) 15

Solução:

Das propriedades de um poliedro convexo e do enunciado do exercício temos que:

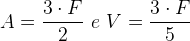
Substituindo esses valores na relação de Euler, teremos o seguinte:

Organizando a equação anterior e resolvendo a equação em F, segue que:

Substituindo o valor da quantidade de faces encontrado na equação das arestas, teremos:

Alternativa b

  

Por Robson Luiz
Professor de Matemática