Diagonal do bloco retangular

Diagonal de um poliedro é um segmento de reta que liga dois de seus vértices não pertencentes a uma mesma face. O cálculo do comprimento dessa diagonal é feito pelo Teorema de Pitágoras. Caso isso seja feito algebricamente, o resultado é uma fórmula capaz de realizar esse cálculo.

Os blocos retangulares são prismas retos cujas bases são retângulos. Esse tipo de prisma apresenta a seguinte propriedade: todas as faces laterais de um prisma reto são retângulos.

Diagonal do bloco retangular

Para encontrar a medida da diagonal do bloco retangular, utilize a seguinte fórmula:

É importante conhecer a estratégia usada para encontrar essa fórmula, pois ela também pode ser usada para encontrar a diagonal do bloco retangular. Essa estratégia está detalhada a seguir:

Encontrando a fórmula pelo teorema de Pitágoras

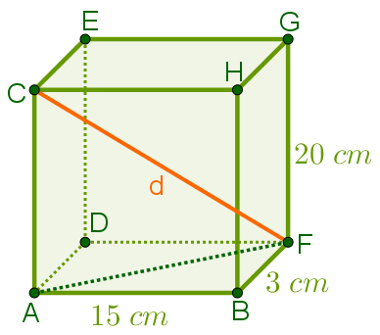
Considere que a imagem a seguir é um bloco retangular, a é seu comprimento; b, sua largura; h, sua altura; e CF, uma de suas diagonais:

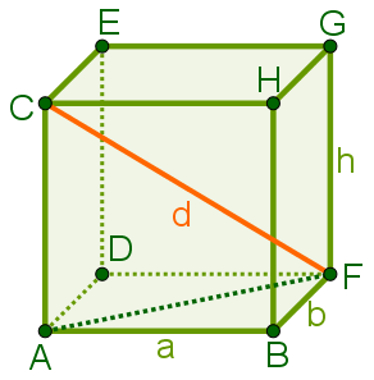
Observe que ACF forma um triângulo retângulo. Além disso, perceba que d (a medida da diagonal do bloco retangular) é também hipotenusa desse triângulo, logo, pode ser obtido pelo teorema de Pitágoras. Entretanto, é necessário conhecer a medida do segmento AF.

Para encontrar essa medida, perceba que ABF também é um triângulo retângulo, e a hipotenusa é justamente o segmento AF. Podemos calculá-lo também pelo teorema de Pitágoras, uma vez que conhecemos as medidas a e b de seus catetos.

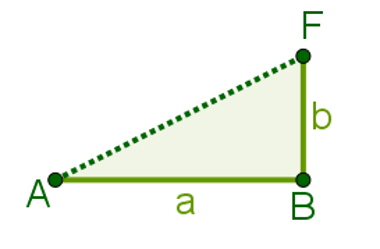
Pelo teorema de Pitágoras:

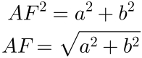
A partir do comprimento de AF, podemos descobrir o comprimento de d, que é a diagonal do bloco retangular. Para isso, observe novamente o triângulo retângulo ACF:

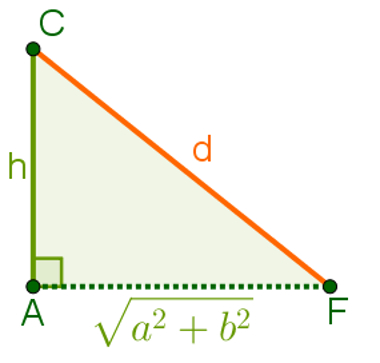
Coloque a medida do segmento AF como feito na imagem acima e use o teorema de Pitágoras para descobrir a medida do segmento d:

Feito isso, utilize as propriedades dos radicais para encontrar:

Dessa maneira, caso seja necessário, utilize o teorema de Pitágoras para descobrir a medida AF do triângulo retângulo; depois, use o mesmo teorema para descobrir a medida da diagonal do bloco retangular.

Exemplo

Um bloco retangular possui 15 cm de comprimento, 3 cm de largura e 20 cm de altura. Calcule a medida da diagonal desse poliedro e, depois, use o teorema de Pitágoras para confirmar seu resultado.

Solução

Com a fórmula, encontraremos a diagonal desse bloco retangular da seguinte maneira:

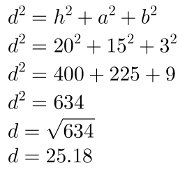
A diagonal mede, aproximadamente, 25,18 cm.

Pelo teorema de Pitágoras, temos:

Vamos calcular a medida de AF com o teorema de Pitágoras:

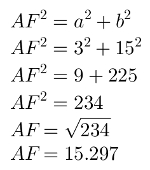
A partir do comprimento do segmento AF, podemos calcular a diagonal do bloco retangular:

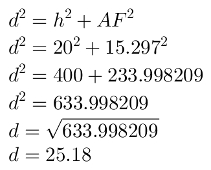
A diagonal mede, aproximadamente, 25,18 cm.

Por Luiz Paulo Moreira
Graduado em Matemática