A calota esférica é o sólido geométrico obtido quando uma esfera é interceptada por um plano, dividindo-a em dois sólidos geométricos. A calota esférica é considerada um corpo redondo, pois, assim como a esfera, possui forma arredondada. Para calcular a área e o volume de uma calota esférica, utilizamos fórmulas específicas.
Leia também: Tronco de cone — o sólido geométrico formado pela parte inferior do cone quando é feita uma secção paralela à base
Tópicos deste artigo
- 1 - Resumo sobre calota esférica
- 2 - O que é calota esférica?
- 3 - Elementos da calota esférica
- 4 - A calota esférica é um poliedro ou um corpo redondo?
- 5 - Como calcular o raio da calota esférica?
- 6 - Como calcular a área da calota esférica?
- 7 - Como calcular o volume da calota esférica?
- 8 - Exercícios resolvidos sobre calota esférica
Resumo sobre calota esférica
- A calota esférica é um sólido geométrico obtido quando a esfera é dividida por um plano.
- Os principais elementos da calota esférica são o raio da esfera, o raio da calota esférica e a altura da calota esférica.
- A calota esférica não é um poliedro, mas sim um corpo redondo.
- Caso o plano divida a esfera ao meio, a calota esférica forma um hemisfério.
- É possível calcular o raio da calota esférica usando o teorema de Pitágoras, organizado da seguinte forma:
\(\left(R-h\right)^2+r^2=R^2\)
- A área da calota esférica pode ser calculada usando a fórmula:
\(A=2\pi rh\ \)
- O volume da calota esférica pode ser calculado por meio da seguinte fórmula:
\(V=\frac{\pi h^2}{3}\cdot\left(3r-h\right)\)
O que é calota esférica?
Calota esférica é o sólido geométrico obtido quando é feita uma secção da esfera com um plano. Quando cortamos a esfera com um plano, dividimos essa esfera em duas calotas esféricas. Quando dividimos a esfera ao meio, a calota esférica é conhecida como hemisfério.
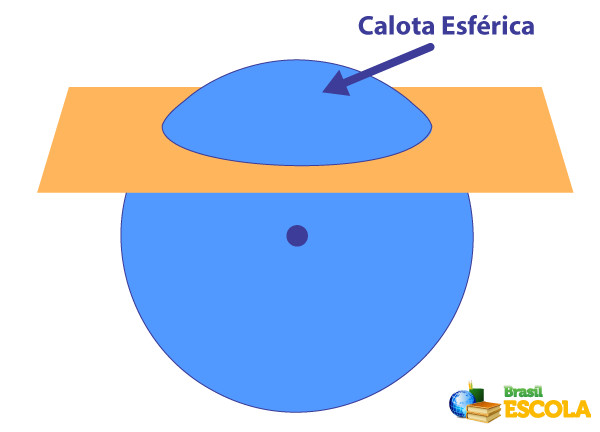
Elementos da calota esférica
Em uma calota esférica, os principais elementos são o raio da esfera, o raio da calota esférica e a altura da calota esférica.
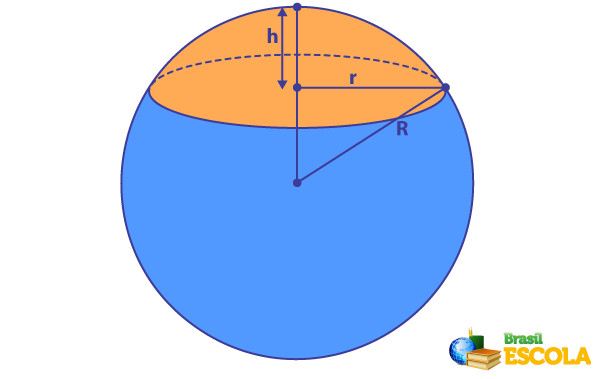
- R → raio da esfera.
- r → raio da calota esférica.
- h → altura da calota esférica.
A calota esférica é um poliedro ou um corpo redondo?
Podemos perceber que a calota é um sólido geométrico. Como possui base circular e superfície arredondada, a calota esférica é considerada um corpo redondo, que também é conhecido como sólido de revolução. Vale ressaltar que o poliedro possui faces formadas por polígonos, o que não é o caso da calota esférica, que possui base formada por um círculo.
Como calcular o raio da calota esférica?
Para calcular o comprimento do raio da calota esférica, é necessário conhecer o comprimento da altura h da calota esférica e o comprimento do raio R da esfera, pois, como podemos ver na imagem a seguir, existe uma relação pitagórica.
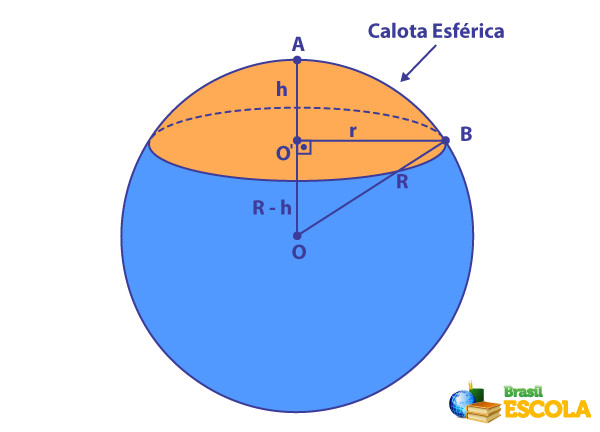
Note que temos um triângulo retângulo, o triângulo OO’B, com hipotenusa medindo R e catetos medindo R – h e r. Aplicando o teorema de Pitágoras, temos que:
\(\left(R-h\right)^2+r^2=R^2\)
Exemplo:
Qual é o raio de uma calota esférica que possui altura de 2 cm, sabendo que o raio da esfera é de 5 cm?
Resolução:
Aplicando a relação pitagórica:
\(\left(R-h\right)^2+r^2=R^2\)
\(\left(5-2\right)^2+r^2=5^2\)
\(3^2+r^2=25\)
\(9+r^2=25\)
\(r^2=25-9\)
\(r^2=16\)
\(r=\sqrt{16}\)
\(r=4\)
Como calcular a área da calota esférica?
Para calcular a área da calota esférica, é necessário conhecer a medida do comprimento do raio R da esfera e da altura h da calota. A fórmula utilizada para calcular a área dessa superfície é:
\(A=2\pi Rh\)
- R → raio da esfera.
- h → altura da calota esférica.
Exemplo:
Uma calota esférica foi obtida de uma esfera que possui 6 cm de raio e altura de 4 cm. Então, qual a área da superfície dessa calota esférica?
Resolução:
Calculando a área da calota esférica, temos que:
\(A=2\pi Rh\)
\(A=2\cdot\pi\cdot6\cdot4\ \)
\(A=48\pi\ cm^2\)
Como calcular o volume da calota esférica?
O volume da calota esférica pode ser calculado de duas maneiras. A primeira fórmula depende do raio R da esfera e da altura h:
\(V=\frac{\pi h^2}{3}\left(3 R-h\right)\)
Exemplo:
Qual é o volume de uma calota esférica obtida de uma esfera com raio de 8 cm cuja altura da calota esférica é de 6 cm?
Resolução:
Como conhecemos o valor de R e h, utilizaremos a primeira fórmula.
R = 8
h = 6
\(V=\frac{\pi h^2}{3}\left(3 R-h\right)\)
\(V=\frac{\pi6^2}{3}\left(3\cdot8-6\right)\)
\(V=\frac{36\pi}{3}\left(24-6\right)\)
\(V=12\pi\left(18\right)\)
\(V=216\pi\ cm^3\)
A outra fórmula de volume da calota esférica leva em consideração o raio da calota esférica r e a altura h da calota:
\(V=\frac{\pi h}{6}\left(3r^2+h^2\right)\)
Exemplo:
Qual é o volume de uma calota esférica que possui raio igual a 10 cm e altura igual a 4 cm?
Resolução:
Nesse caso, temos que r = 10 cm e que h = 4 cm. Como conhecemos o valor do raio da calota esférica e da altura, utilizaremos a segunda fórmula:
\(V=\frac{\pi h}{6}\left(3r^2+h^2\right)\)
\(V=\frac{4\pi}{6}\left(3{\cdot10}^2+4^2\right)\)
\(V=\frac{4\pi}{6}\left(3\cdot100+16\right)\)
\(V=\frac{4\pi}{6}\left(300+16\right)\)
\(V=\frac{4\pi}{6}\left(316\right)\)
\(V=\frac{1264\pi}{6}\)
\(V\approx210,7\ \pi\ cm³\)
Exercícios resolvidos sobre calota esférica
Questão 1
(Enem) Para decorar uma mesa de festa infantil, um chefe de cozinha usará um melão esférico com diâmetro medindo 10 cm, o qual servirá de suporte para espetar diversos doces. Ele vai retirar uma calota esférica do melão, conforme ilustra a figura, e, para garantir a estabilidade desse suporte, dificultando que o melão role sobre a mesa, o chef fará o corte de modo que o raio r da seção circular de corte seja de pelo menos 3 cm. Por outro lado, o chefe desejará dispor da maior área possível da região em que serão afixados os doces.
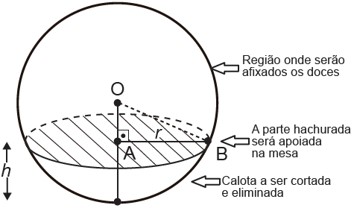
Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão em uma altura h, em centímetro, igual a
A) \(5-\frac{\sqrt{91}}{2}\)
B) \( 10-\sqrt{91}\)
C) 1
D) 4
E) 5
Resolução:
Alternativa C
Sabemos que o diâmetro da esfera mede 10 cm, logo o seu raio é 5 cm, então OB = 5 cm.
Se o raio da secção é de exatamente 3 cm, temos que:
AO² +AB² = OB²
AO² + 3² = 5²
AO² + 9 = 25
AO² = 25 – 9
AO² = 16
AO = \(\sqrt{16}\)
AO = 4 cm
Portanto:
h + 4 = 5
h = 5 – 4
h = 1
Questão 2
Uma calota esférica possui área igual a 144π cm². Sabendo que ela possui 9 cm de raio, a medida da altura dessa calota esférica é:
A) 8 cm
B) 10 cm
C) 14 cm
D) 16 cm
E) 22 cm
Resolução:
Alternativa A
Sabemos que:
\(A=2\pi Rh\)
\(144\pi=2\pi\cdot9\cdot h\)
\(144\pi=18\pi h\)
\(\frac{144\pi}{18\pi}=h\)
\(8=h\)
A altura é de 8 cm.
Por Raul Rodrigues de Oliveira
Professor de Matemática

