A posição relativa entre duas figuras é o estudo das possibilidades de relação entre figuras geométricas dentro de um espaço dado. Não é necessário que esse espaço seja tridimensional. Na geometria plana, todas as figuras geométricas pertencem a um espaço que costumamos chamar de plano.
Ao observar o plano como um objeto pertencente ao espaço, esse espaço deve ter, no mínimo, uma dimensão a mais que o plano. Assim, como o plano é um objeto que possui duas dimensões, a análise das posições relativas entre outro objeto qualquer desse plano deverá ser feita, no mínimo, no espaço tridimensional.
Uma reta qualquer possui três possibilidades de interação com o plano. Essas possibilidades são conhecidas como posições relativas entre uma reta e um plano e estão listadas a seguir:
Reta contida no plano
Dizemos que uma reta está contida no plano quando todos os seus pontos também são pontos do plano. Também é possível dizer que o plano contém a reta. A linguagem é a mesma utilizada para conjuntos numéricos.
O que garante que uma reta esteja contida no plano é o postulado da inclusão, que afirma o seguinte: Se um plano contém dois pontos de uma reta, então toda a reta está contida nesse plano. Esse fato não pode ser provado, mas deve ser aceito como verdadeiro, pois ele compõe as bases da Geometria. Por isso, é chamado de postulado ou axioma.
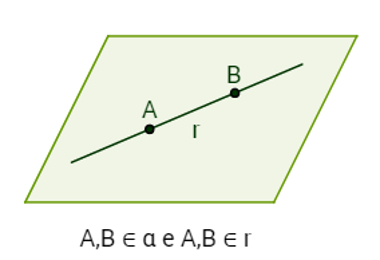
Reta r pertencente (contida) ao plano α
Reta e plano concorrentes
Também chamada de secante, essa posição refere-se a uma reta e um plano que possuem um único ponto em comum. Esse fato é garantido pelo postulado da existência, que diz: Existem infinitos pontos contidos em um plano e também fora dele. Como esse postulado garante a existência de pelo menos um ponto no plano e um fora dele, por meio do postulado da determinação, podemos dizer que: dois pontos distintos determinam uma única reta que passa por eles, assim, provamos a existência de uma reta que possui apenas um ponto comum ao plano.
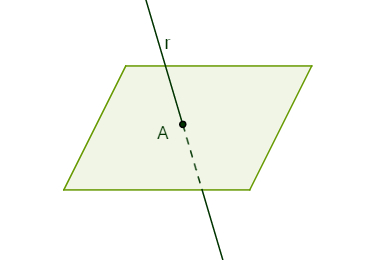
Reta r concorrente (ou secante) ao plano α
Uma reta secante a um plano pelo ponto A e que forma um ângulo de 90° com qualquer reta pertencente a esse plano que contenha o ponto A é chamada de reta perpendicular (ou ortogonal) ao plano.
Reta e plano paralelos
Reta e plano são paralelos quando eles não possuem nenhum ponto em comum.
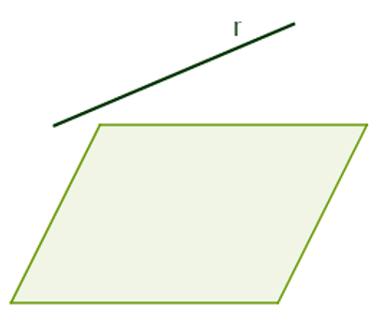
Reta r paralela ao plano α
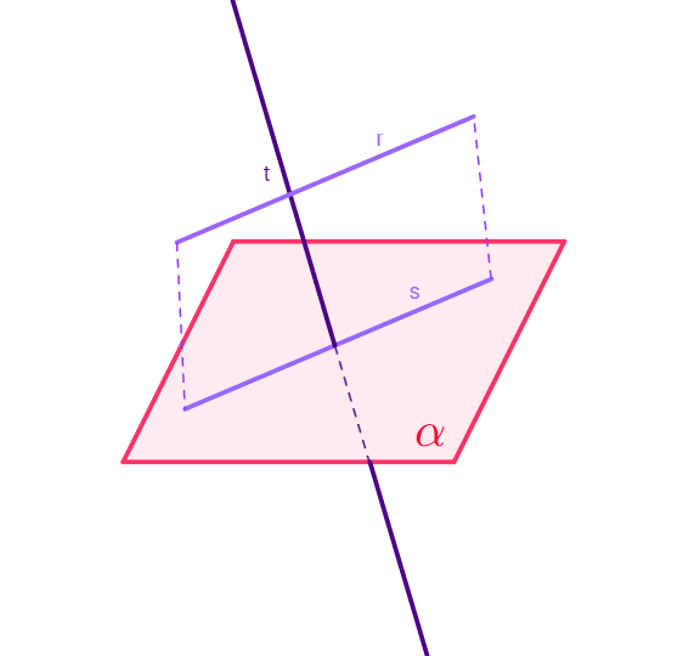
Tendo em mente o quinto postulado de Euclides (dada uma reta e um ponto não pertencente a ela, pelo ponto passa uma única reta paralela à reta dada), é possível concluir a seguinte propriedade de paralelismo entre reta e plano: Se uma reta r não pertence nem é concorrente ao plano α, mas é paralela a uma reta s contida nesse plano, então a reta r é paralela ao plano α.
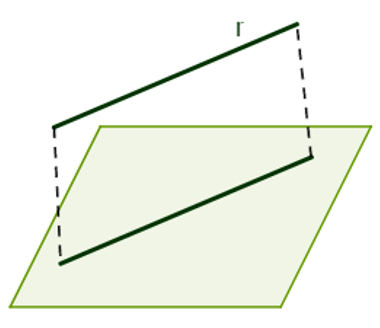
A reta r é paralela à reta s, que pertence ao plano α, logo, r é paralela a α
Por Luiz Paulo Moreira
Graduado em Matemática